A grammar is a set of production rules which are used to generate strings of a language. In this article, we have discussed how to find the language generated by a grammar and vice versa as well.
Language generated by a grammar –
Given a grammar G, its corresponding language L(G) represents the set of all strings generated from G. Consider the following grammar,
G: S-> aSb|ε
In this grammar, using S-> ε, we can generate ε. Therefore, ε is part of L(G). Similarly, using S=>aSb=>ab, ab is generated. Similarly, aabb can also be generated.
Therefore,
L(G) = {anbn, n>=0}
In language L(G) discussed above, the condition n = 0 is taken to accept ε.
Key Points –
- For a given grammar G, its corresponding language L(G) is unique.
- The language L(G) corresponding to grammar G must contain all strings which can be generated from G.
- The language L(G) corresponding to grammar G must not contain any string which can not be generated from G.
Let us discuss questions based on this:
Que-1. Consider the grammar: (GATE-CS-2009)
S -> aSa|bSb|a|b
The language generated by the above grammar over the alphabet {a,b} is the set of:
(A) All palindromes
(B) All odd length palindromes.
(C) Strings that begin and end with the same symbol
(D) All even length palindromes
Solution: Using S->a and S->b, a and b can be generated. Similarly using S=>aSa=>aba, aba can be generated. Other strings which can be generated from grammar are: a, b, aba, bab, aaa, bbb, ababa, …
Therefore, option (B) is correct.
Que-2. Consider the following context-free grammars: (GATE-CS-2016)
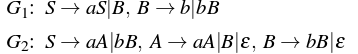
Which one of the following pairs of languages is generated by G1 and G2, respectively?

Solution: Consider the grammar G1:
Using S=>B=>b, b can be generated.
Using S=>B=>bB, bb can be generated.
Using S=>aS=>aB=>ab can be generated.
Using S=>aS=>aB=>abB=>abb can be generated.
As we can see, number of a’s can be zero or more but number of b is always greater than zero.
Therefore,
L(G1) = {ambn| m>=0 and n>0}
Consider the grammar G2:
Using S=>aA=>a, a can be generated.
Using S=>bB=>b, b can be generated.
Using S=>aA=>aaA=>aa can be generated.
Using S=>bB=>bbB=>bb can be generated.
Using S=>aA=>aB=>abB=>abb can be generated.
As we can see, either a or b must be greater than 0.
Therefore,
L(G2) = {ambn| m>0 or n>0}
Grammar generating a given language –
Given a language L(G), its corresponding grammar G represents the production rules which produces L(G). Consider the language L(G):
L(G) = {anbn, n>=0}
The language L(G) is set of strings ε, ab, aabb, aaabbb….
For ε string in L(G), the production rule can be S->ε.
For other strings in L(G), the production rule can be S->aSb|ε.
Therefore, grammar G corresponding to L(G) is:
S->aSb| ε
Key Points –
- For a given language L(G), there can be more than one grammar which can produce L(G).
- The grammar G corresponding to language L(G) must generate all possible strings of L(G).
- The grammar G corresponding to language L(G) must not generate any string which is not part of L(G).
Let us discuss questions based on this:
Que-3. Which one of the following grammar generates the language L = {ai b j | i≠j}? (GATE-CS-2006)

Solution: The given language L contains the strings :
{a, b, aa, bb, aaa, bbb, aab, abb…}
It means either the string must contain one or more number of a OR one or more number of b OR a followed by b having unequal number of a and b.
If we consider grammar in option (A), it can generate ab as:
S=>AC=>aAC=>aC=>ab
However, ab can’t be generated by language L. Therefore, grammar in option (A) is not correct.
Similarly, grammar in option (B) can generate ab as:
S=>aS=>ab
However, ab can’t be generated by language L. Therefore, grammar in option (B) is not correct.
Similarly, grammar in option (C) can generate ab as:
S=>AC=>C=>aCb=>ab
However, ab can’t be generated by language L. Therefore, grammar in option (C) is not correct.
Therefore, using method of elimination, option (D) is correct.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...