The Malevolent Mathemagician | Natural Language Programming
Last Updated :
19 Sep, 2023
A long, long time ago, when I was in seventh grade, a guest speaker came to our math class. We were all very excited to hear him speak, but I was a little sad because my friend Zeno was sent to detention just before the presentation was to begin. Nobody knew why. Anyway, the guest speaker’s name was Mr Georg. He started by asking the class if we thought there were (a) more odd numbers, or (b) more even numbers, or (c) more of both put together. We all said, “More of both put together.” And it was then that Mr Georg got very red in the face and shouted, “No. No! NO!” Then he turned and started scribbling on the chalk board, mumbling to himself about Hebrew letters the whole time. This, best I can remember, is what he wrote (redrawn in our built-in WYSIWYG page editor): 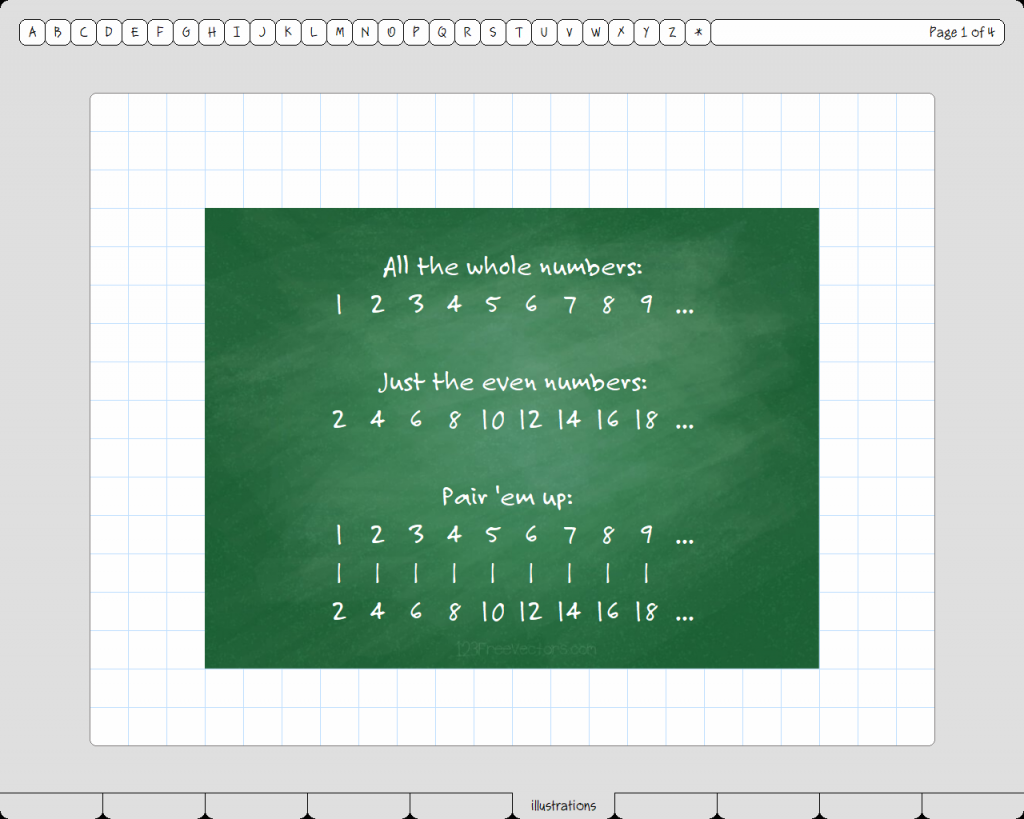 It seemed like all that writing calmed him down a bit, and he turned back to the class and said, softly but sternly, “I hope you little idiots can now see that you are wrong. The number of even numbers, and the number of odd numbers, and the number of both together are all the same!” It was then that my deskmate, Leopold (the smartest kid in our class), whispered to me, “I’m not buying it. I think this guy is nuts.” I shushed him because Mr Georg was mumbling and writing on the chalkboard again, and I wanted to hear what he was saying. But Leopold said, “Be careful, friend. I suspect this man is not just a Mathemagician, but a Malevolent Mathemagician, a corrupter of youth.” This time Mr Georg wrote something like this:
It seemed like all that writing calmed him down a bit, and he turned back to the class and said, softly but sternly, “I hope you little idiots can now see that you are wrong. The number of even numbers, and the number of odd numbers, and the number of both together are all the same!” It was then that my deskmate, Leopold (the smartest kid in our class), whispered to me, “I’m not buying it. I think this guy is nuts.” I shushed him because Mr Georg was mumbling and writing on the chalkboard again, and I wanted to hear what he was saying. But Leopold said, “Be careful, friend. I suspect this man is not just a Mathemagician, but a Malevolent Mathemagician, a corrupter of youth.” This time Mr Georg wrote something like this: 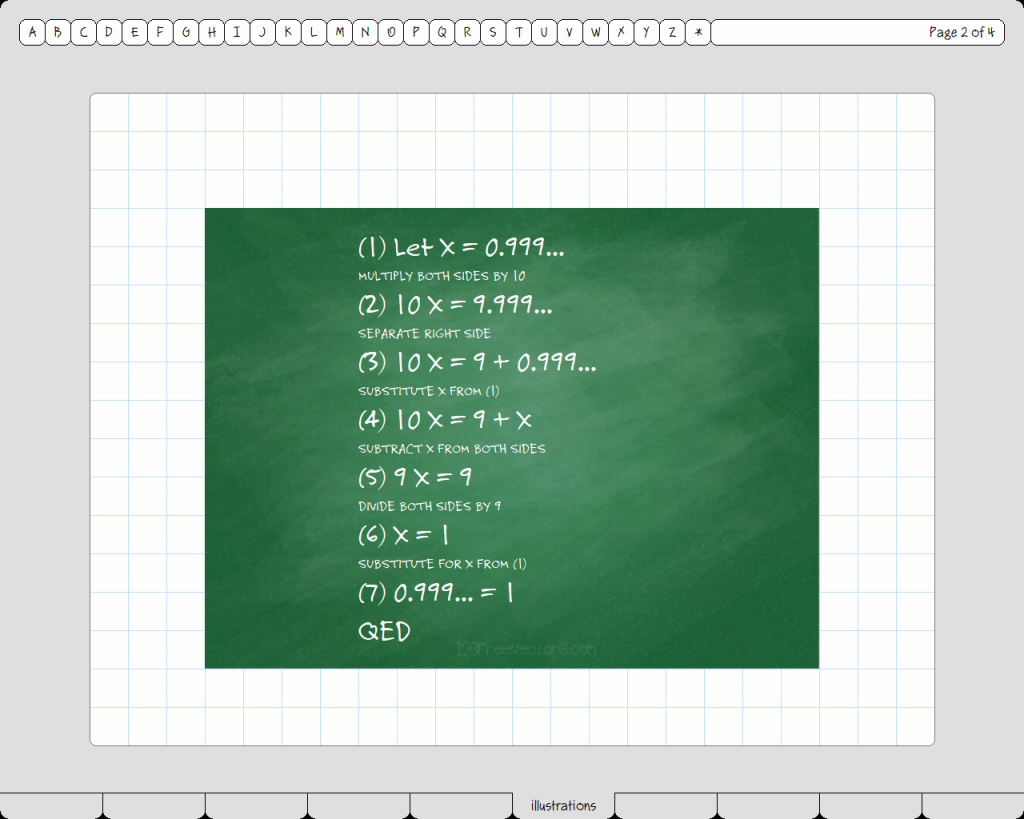 When Mr Georg was finished scribbling, Leopold glanced at the board and then whispered to me, “I don’t know if this charlatan is talking philosophy or theology, but I’m pretty sure there’s no mathematics there.” But now Mr Georg had found a yardstick and was using it to draw really nifty and precise pictures on the board. Something like this, if I remember correctly, which I thought made a lot of sense:
When Mr Georg was finished scribbling, Leopold glanced at the board and then whispered to me, “I don’t know if this charlatan is talking philosophy or theology, but I’m pretty sure there’s no mathematics there.” But now Mr Georg had found a yardstick and was using it to draw really nifty and precise pictures on the board. Something like this, if I remember correctly, which I thought made a lot of sense: 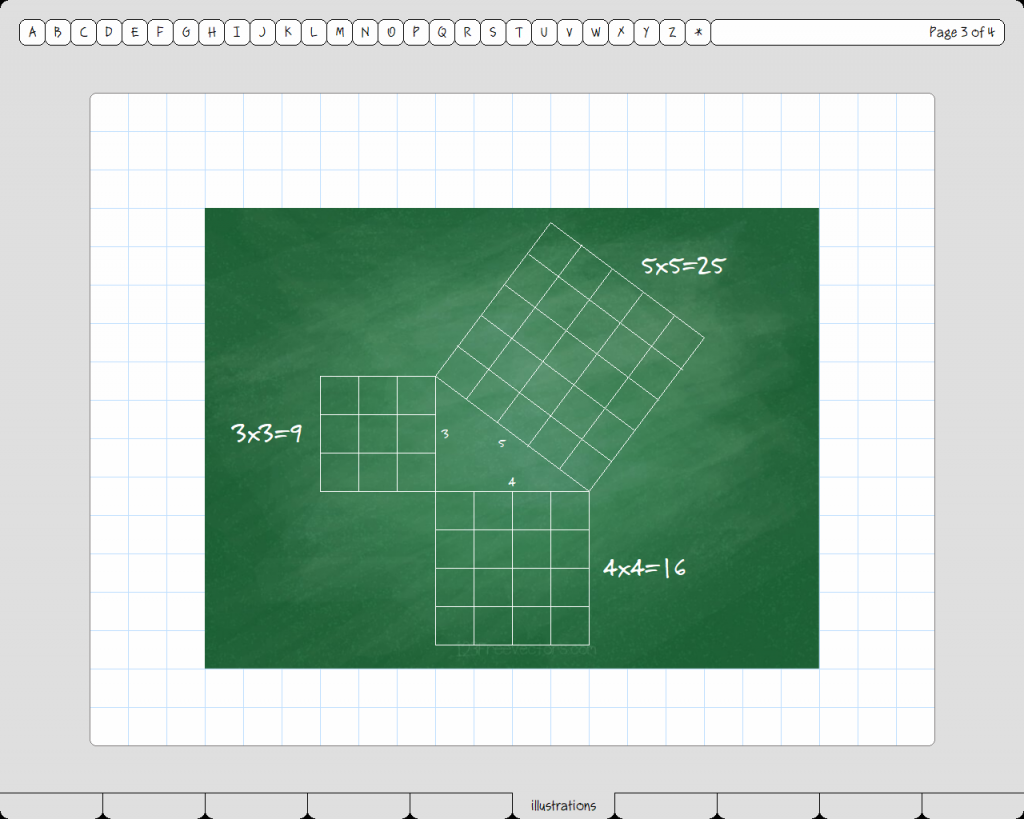 I had just finished copying it down when Leopold whispered, “Ask him to draw the picture for a triangle with both of the short sides just one unit long.” Hoping to get Leopold to stop whispering, I raised my hand and posed the question. But instead of drawing the picture I asked for, Mr Georg erased the board and drew a triangle with the sides labeled a, b, and c. Then he started writing mathemagical formulas on the board as he mumbled names that sounded like Greek to me.
I had just finished copying it down when Leopold whispered, “Ask him to draw the picture for a triangle with both of the short sides just one unit long.” Hoping to get Leopold to stop whispering, I raised my hand and posed the question. But instead of drawing the picture I asked for, Mr Georg erased the board and drew a triangle with the sides labeled a, b, and c. Then he started writing mathemagical formulas on the board as he mumbled names that sounded like Greek to me. 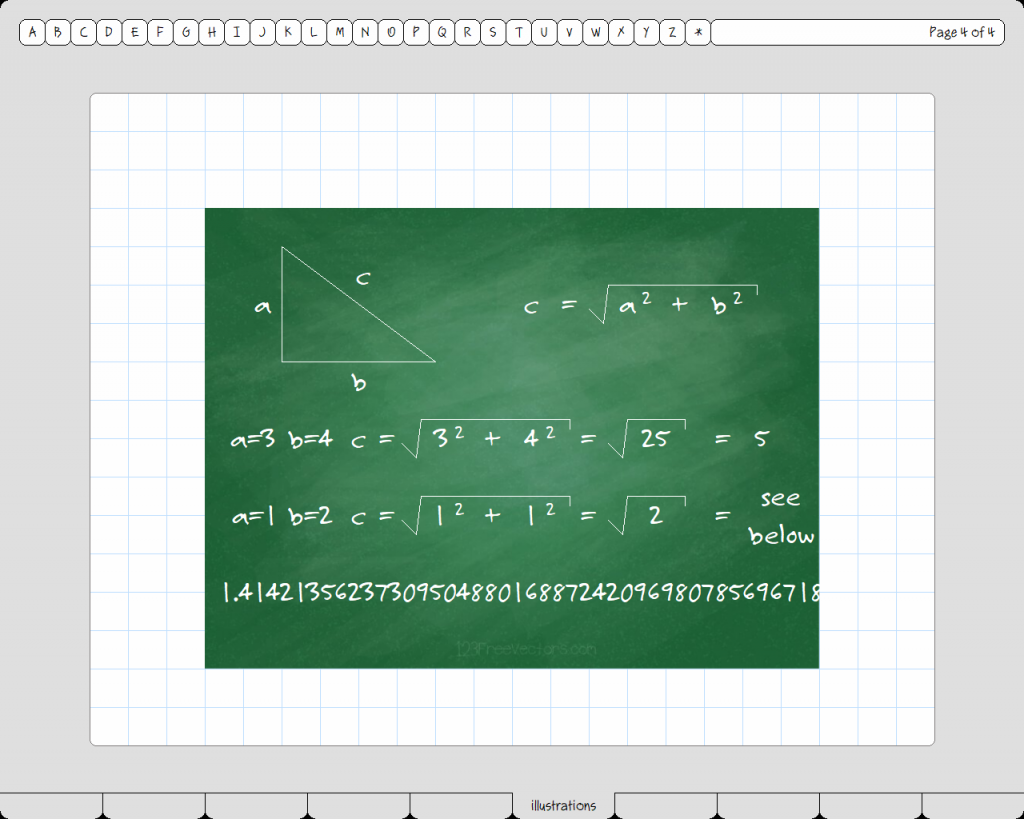 Then he got a stick and tapped on the board as he showed us how the length of the long side of a right triangle was equal to the square root of the sum of the squares of the other two sides, and “proved” that he was right by letting a=3 and b=4 and using his formula to calculate c=5. Then he harrumphed and said, “Now I will answer that little mutt’s question.” So he let a=1 and b=1 and plugged the numbers into his formula. Then he knelt down and started writing the value for c. It was a very long number, and it took him quite a while to calculate it in his head. Sally in the front row asked him where he was getting all those digits and he stopped just long enough to reply, “It’s a technique that is clearly beyond your understanding, little girl. Perhaps you should be in art class.” Then Leopold leaned over to whisper to me again, but I said, “If you have a question, Leo, ask him, not me.” So he did. Without waiting to be called on, he shouted, “Are you really asking us to believe that the lengths of the sides of a 3-4-5 right triangle are all whole numbers, exact (in some unit of measure), and easily calculated; but that the long side of a right triangle whose other sides are one unit long, can only be represented by a different kind of number altogether? A number that is both inexact and very difficult to compute? Is that what you’re selling here?” Mr. Georg hesitated, and our teacher, to fill the silence, said, “Leopold, you will now join Zeno in detention.” But on the way out Leo turned and shouted back at the class, “The good God created the whole numbers; all else is menshenwerk!” And that was the day two things happened in my head. First, I began to suspect that there was some shady sleight-of-hand in the whole mathemagical shebang, however popular and useful it appears to be. Second, I began to dream of a day when a different way of understanding problems such as these might be discovered. So I got myself a degree in mathemagics (mainly by keeping my mouth shut)…
Then he got a stick and tapped on the board as he showed us how the length of the long side of a right triangle was equal to the square root of the sum of the squares of the other two sides, and “proved” that he was right by letting a=3 and b=4 and using his formula to calculate c=5. Then he harrumphed and said, “Now I will answer that little mutt’s question.” So he let a=1 and b=1 and plugged the numbers into his formula. Then he knelt down and started writing the value for c. It was a very long number, and it took him quite a while to calculate it in his head. Sally in the front row asked him where he was getting all those digits and he stopped just long enough to reply, “It’s a technique that is clearly beyond your understanding, little girl. Perhaps you should be in art class.” Then Leopold leaned over to whisper to me again, but I said, “If you have a question, Leo, ask him, not me.” So he did. Without waiting to be called on, he shouted, “Are you really asking us to believe that the lengths of the sides of a 3-4-5 right triangle are all whole numbers, exact (in some unit of measure), and easily calculated; but that the long side of a right triangle whose other sides are one unit long, can only be represented by a different kind of number altogether? A number that is both inexact and very difficult to compute? Is that what you’re selling here?” Mr. Georg hesitated, and our teacher, to fill the silence, said, “Leopold, you will now join Zeno in detention.” But on the way out Leo turned and shouted back at the class, “The good God created the whole numbers; all else is menshenwerk!” And that was the day two things happened in my head. First, I began to suspect that there was some shady sleight-of-hand in the whole mathemagical shebang, however popular and useful it appears to be. Second, I began to dream of a day when a different way of understanding problems such as these might be discovered. So I got myself a degree in mathemagics (mainly by keeping my mouth shut)…  …and let the important matters stew in the back of my brain for several decades. I recently discovered that there are others of my ilk, like Master Norman, who wrote this book on the subject:
…and let the important matters stew in the back of my brain for several decades. I recently discovered that there are others of my ilk, like Master Norman, who wrote this book on the subject:  . But when it came to dealing with trigonometry in our whole-number-only Plain English programming language, I was still looking for something even simpler. I will now describe what steps we’ve taken, which, I admit, are only baby steps toward a more natural and more rational mathematics. We began by borrowing some ideas from non-mathemagicians, like old-time roofers and ancient explorers. From the roofers we got the idea that angles can be expressed in “rise over run” terms (instead of degrees); and from explorers we got the idea for something more natural than the infamous “unit circle” of the mathemagic world: the compass. This is a picture of our Osmosian compass:
. But when it came to dealing with trigonometry in our whole-number-only Plain English programming language, I was still looking for something even simpler. I will now describe what steps we’ve taken, which, I admit, are only baby steps toward a more natural and more rational mathematics. We began by borrowing some ideas from non-mathemagicians, like old-time roofers and ancient explorers. From the roofers we got the idea that angles can be expressed in “rise over run” terms (instead of degrees); and from explorers we got the idea for something more natural than the infamous “unit circle” of the mathemagic world: the compass. This is a picture of our Osmosian compass:  Note that zero is at the top, not the right, that headings increase in the clockwise direction, and that all the way around is 384 points, not 360 degrees. If you’re curious, this is the whole-number-only Plain English routine that draws that image:
Note that zero is at the top, not the right, that headings increase in the clockwise direction, and that all the way around is 384 points, not 360 degrees. If you’re curious, this is the whole-number-only Plain English routine that draws that image:
Now let’s draw some triangles. Here’s a simple 3-4-5 triangle with the center of the screen marked by a red dot… 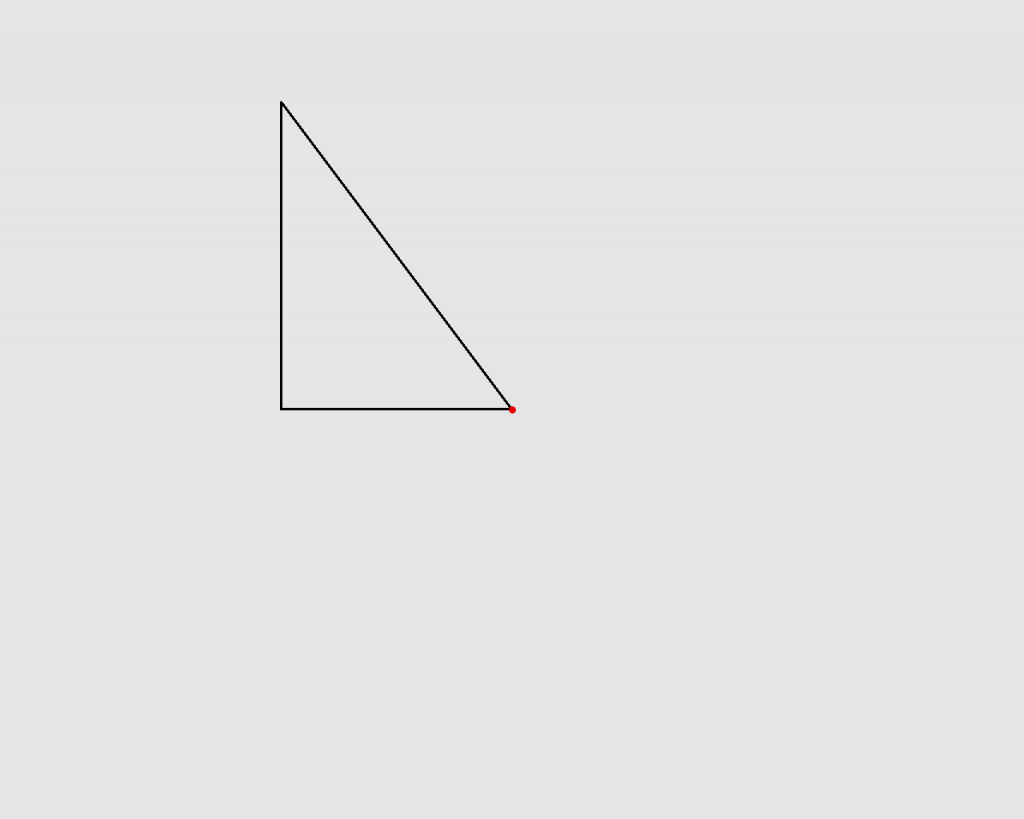 …and this is the routine that drew it:
…and this is the routine that drew it:
The critical juncture in this routine occurs after we’ve drawn the 3-inch horizontal line and the 4-inch vertical line. At that point we’re sitting on the uppermost vertex of the triangle, facing north. To get back to the center of the screen we need two things. Mathemagicians would say, “Of course you do. You need to know how far to turn around (an angle) and how long your next stroke should be. But we don’t want to say that, for two reasons: first, because it hurts our heads to figure out exactly what angle we need, and secondly because it can be difficult (or even impossible) to figure out the exact stroke length using mathemagical techniques. “If it’s hard, it’s wrong, ” is a standing motto among us Osmosians. So back to the third stroke of our triangle. Exactly where are we? We’re 4 inches north of center (that’s the rise) and three inches west of center (that’s the run). That’s our exact position. In what direction do we want to go? Obviously, we want to go 4 inches south and 3 inches east, by the shortest possible route. And exactly how far do we want to go? Same answer: 4 inches south and 3 inches east. Isn’t it curious that both the angle of our line and the length of our line can be described in the same, whole-number-only terms? And note that this works, not only for “mathemagician-friendly” 3-4-5 triangles, but for all triangles. So all we need to do is compute the rise and the run, which is simply the difference between two spots on the screen…
…and then we stroke the third line based on that rise/run:
At the very bottom we’ve got Bresenham’s integer-only line drawing algorithm, so we’re not cheating when we plot the lines. So far, so good. Now let’s see if it actually works with that troublesome “unit triangle” — a right triangle with short sides just one unit in length. The routine to draw it is the same as above, except that the first two strokes are only one inch long:
Here’s the output:  Whoohoo! It works! And what is the exact length of those sides? Let me see… the first side has a rise of exactly 0 and a run of exactly -1; the second side has a rise of exactly 1 and a run of exactly 0. And the third side has rise of exactly -1 and a run of exactly 1. All integers, all exact, all easily calculated. But will it work if the triangle is not a right triangle, or is rotated in some arbitrary direction? Let’s see. Here’s a routine that draws eight, scalene triangles at eight different rotations:
Whoohoo! It works! And what is the exact length of those sides? Let me see… the first side has a rise of exactly 0 and a run of exactly -1; the second side has a rise of exactly 1 and a run of exactly 0. And the third side has rise of exactly -1 and a run of exactly 1. All integers, all exact, all easily calculated. But will it work if the triangle is not a right triangle, or is rotated in some arbitrary direction? Let’s see. Here’s a routine that draws eight, scalene triangles at eight different rotations:
And here’s the output:  Baby steps toward a more natural, more rational mathematics. BIG baby steps. In Plain English.
Baby steps toward a more natural, more rational mathematics. BIG baby steps. In Plain English.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...