The biggest possible circle that can be inscribed in a rectangle
Last Updated :
18 Sep, 2022
Given a rectangle of length l & breadth b, we have to find the largest circle that can be inscribed in the rectangle.
Examples:
Input : l = 4, b = 8
Output : 12.56
Input : l = 16 b = 6
Output : 28.26
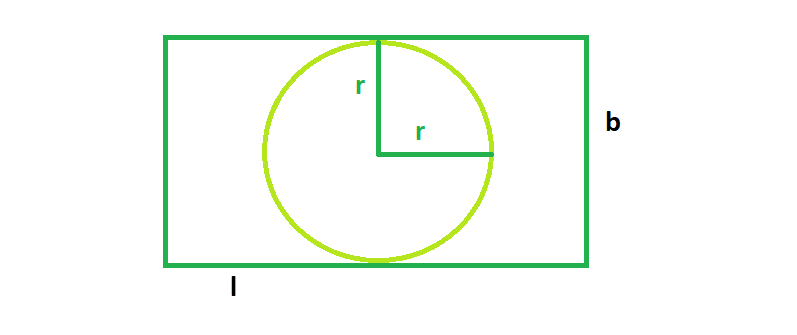
From the figure, we can see, the biggest circle that could be inscribed in the rectangle will have radius always equal to the half of the shorter side of the rectangle. So from the figure,
radius, r = b/2 &
Area, A = ? * (r^2)
C++
#include <bits/stdc++.h>
using namespace std;
float circlearea(float l, float b)
{
if (l < 0 || b < 0)
return -1;
if (l < b)
return 3.14 * pow(l / 2, 2);
else
return 3.14 * pow(b / 2, 2);
}
int main()
{
float l = 4, b = 8;
cout << circlearea(l, b) << endl;
return 0;
}
|
Java
class GFG
{
static float circlearea(float l,
float b)
{
if (l < 0 || b < 0)
return -1;
if (l < b)
return (float)(3.14 * Math.pow(l / 2, 2));
else
return (float)(3.14 * Math.pow(b / 2, 2));
}
public static void main(String[] args)
{
float l = 4, b = 8;
System.out.println(circlearea(l, b));
}
}
|
Python 3
def circlearea(l, b):
if (l < 0 or b < 0):
return -1
if (l < b):
return 3.14 * pow(l // 2, 2)
else:
return 3.14 * pow(b // 2, 2)
if __name__ == "__main__":
l = 4
b = 8
print(circlearea(l, b))
|
C#
using System;
class GFG
{
static float circlearea(float l,
float b)
{
if (l < 0 || b < 0)
return -1;
if (l < b)
return (float)(3.14 * Math.Pow(l / 2, 2));
else
return (float)(3.14 * Math.Pow(b / 2, 2));
}
public static void Main()
{
float l = 4, b = 8;
Console.Write(circlearea(l, b));
}
}
|
PHP
<?php
function circlearea($l, $b)
{
if ($l < 0 || $b < 0)
return -1;
if ($l < $b)
return 3.14 * pow($l / 2, 2);
else
return 3.14 * pow($b / 2, 2);
}
$l = 4;
$b = 8;
echo circlearea($l, $b)."\n";
?>
|
Javascript
<script>
function circlearea(l, b)
{
if (l < 0 || b < 0)
return -1;
if (l < b)
return (3.14 * Math.pow(l / 2, 2));
else
return (3.14 * Math.pow(b / 2, 2));
}
var l = 4, b = 8;
document.write(circlearea(l, b));
</script>
|
Time complexity: O(1) as it is doing constant operations
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...