Ternary representation of Cantor set
Last Updated :
06 Sep, 2022
Given three integers A, B and L, the task is to print the ternary cantor set from range [A, B] upto L levels.
Ternary Cantor Set: A ternary Cantor set is a set built by removing the middle part of a line segment when divided into 3 parts and repeating this process with the remaining shorter segments. Below is an illustration of a cantor set.

An illustration of a Ternary Cantor Set
Examples:
Input: A = 0, B = 1, L = 2
Output:
Level 0: [0.000000] — [1.000000]
Level 1: [0.000000] — [0.333333] [0.666667] — [1.000000]
Level 2: [0.000000] — [0.111111] [0.222222] — [0.333333] [0.666667] — [0.777778] [0.888889] — [1.000000]
Explanation: For the given range [0, 1], in level 1, it is divided into three parts ([0, 0.33], [0.33, 0.67], [0.67, 1]). From the three parts, the middle part is ignored. This process is continued for every part in the subsequent executions.
Input: A = 0, B = 9, L = 3
Output:
Level_0: [0.000000] — [9.000000]
Level_1: [0.000000] — [3.000000] [6.000000] — [9.000000]
Level_2: [0.000000] — [1.000000] [2.000000] — [3.000000] [6.000000] — [7.000000] [8.000000] — [9.000000]
Level_3: [0.000000] — [0.333333] [0.666667] — [1.000000] [2.000000] — [2.333333] [2.666667] — [3.000000] [6.000000] — [6.333333] [6.666667] — [7.000000] [8.000000] — [8.333333] [8.666667] — [9.000000]
Approach:
- Create a linked list data structure for each node of the Set, having the start value, end value and a pointer to the next node.
- Initialize the list with the start and end value given as the input.
- For the next level:
- Create a new node where the difference between the start and end values is
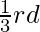 of the initial, i.e. start value is
of the initial, i.e. start value is 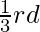 less than the initial end value.
less than the initial end value. - Further, modify the original node, such that the end value is
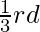 more of the initial start value.
more of the initial start value. - Place the pointer to the new node after the original one accordingly
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
typedef struct cantor {
double start, end;
struct cantor* next;
} Cantor;
Cantor* startList(Cantor* head,
double start_num,
double end_num)
{
if (head == NULL) {
head = new Cantor;
head->start = start_num;
head->end = end_num;
head->next = NULL;
}
return head;
}
Cantor* propagate(Cantor* head)
{
Cantor* temp = head;
if (temp != NULL) {
Cantor* newNode
= new Cantor;
double diff
= (((temp->end) - (temp->start)) / 3);
newNode->end = temp->end;
temp->end = ((temp->start) + diff);
newNode->start = (newNode->end) - diff;
newNode->next = temp->next;
temp->next = newNode;
propagate(temp->next->next);
}
return head;
}
void print(Cantor* temp)
{
while (temp != NULL) {
printf("[%lf] -- [%lf]\t",
temp->start, temp->end);
temp = temp->next;
}
cout << endl;
}
void buildCantorSet(int A, int B, int L)
{
Cantor* head = NULL;
head = startList(head, A, B);
for (int i = 0; i < L; i++) {
cout <<"Level_"<< i<<" : ";
print(head);
propagate(head);
}
cout <<"Level_"<< L<<" : ";
print(head);
}
int main()
{
int A = 0;
int B = 9;
int L = 2;
buildCantorSet(A, B, L);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct cantor {
double start, end;
struct cantor* next;
} Cantor;
Cantor* startList(Cantor* head,
double start_num,
double end_num)
{
if (head == NULL) {
head = (Cantor*)malloc(sizeof(Cantor));
head->start = start_num;
head->end = end_num;
head->next = NULL;
}
return head;
}
Cantor* propagate(Cantor* head)
{
Cantor* temp = head;
if (temp != NULL) {
Cantor* newNode
= (Cantor*)malloc(sizeof(Cantor));
double diff
= (((temp->end) - (temp->start)) / 3);
newNode->end = temp->end;
temp->end = ((temp->start) + diff);
newNode->start = (newNode->end) - diff;
newNode->next = temp->next;
temp->next = newNode;
propagate(temp->next->next);
}
return head;
}
void print(Cantor* temp)
{
while (temp != NULL) {
printf("[%lf] -- [%lf]\t",
temp->start, temp->end);
temp = temp->next;
}
printf("\n");
}
void buildCantorSet(int A, int B, int L)
{
Cantor* head = NULL;
head = startList(head, A, B);
for (int i = 0; i < L; i++) {
printf("Level_%d : ", i);
print(head);
propagate(head);
}
printf("Level_%d : ", L);
print(head);
}
int main()
{
int A = 0;
int B = 9;
int L = 2;
buildCantorSet(A, B, L);
return 0;
}
|
Java
class GFG
{
static class Cantor
{
double start, end;
Cantor next;
};
static Cantor Cantor;
static Cantor startList(Cantor head, double start_num,
double end_num)
{
if (head == null)
{
head = new Cantor();
head.start = start_num;
head.end = end_num;
head.next = null;
}
return head;
}
static Cantor propagate(Cantor head)
{
Cantor temp = head;
if (temp != null)
{
Cantor newNode = new Cantor();
double diff = (((temp.end) - (temp.start)) / 3);
newNode.end = temp.end;
temp.end = ((temp.start) + diff);
newNode.start = (newNode.end) - diff;
newNode.next = temp.next;
temp.next = newNode;
propagate(temp.next.next);
}
return head;
}
static void print(Cantor temp)
{
while (temp != null)
{
System.out.printf("[%f] -- [%f]", temp.start, temp.end);
temp = temp.next;
}
System.out.printf("\n");
}
static void buildCantorSet(int A, int B, int L)
{
Cantor head = null;
head = startList(head, A, B);
for (int i = 0; i < L; i++)
{
System.out.printf("Level_%d : ", i);
print(head);
propagate(head);
}
System.out.printf("Level_%d : ", L);
print(head);
}
public static void main(String[] args)
{
int A = 0;
int B = 9;
int L = 2;
buildCantorSet(A, B, L);
}
}
|
Python3
class Cantor:
def __init__(self):
self.start = 0;
self.end = 0;
self.next = None;
cantor = None;
def startList(head, start_num, end_num):
if (head == None) :
head = Cantor();
head.start = start_num;
head.end = end_num;
head.next = None;
return head;
def propagate(head):
temp = head;
if (temp != None):
newNode = Cantor();
diff = (((temp.end) - (temp.start)) / 3);
newNode.end = temp.end;
temp.end = ((temp.start) + diff);
newNode.start = (newNode.end) - diff;
newNode.next = temp.next;
temp.next = newNode;
propagate(temp.next.next);
return head;
def Print(temp):
while (temp != None) :
print("[", temp.start, "] -- [", temp.end, "] ", sep = "", end = "");
temp = temp.next;
print()
def buildCantorSet(A, B, L):
head = None;
head = startList(head, A, B);
for i in range(L):
print("Level_", i, " : ", sep = "", end = "");
Print(head);
propagate(head);
print("Level_", L, " : ", end = "", sep = "");
Print(head);
A = 0;
B = 9;
L = 2;
buildCantorSet(A, B, L);
|
C#
using System;
class GFG
{
class Cantor
{
public double start, end;
public Cantor next;
};
static Cantor cantor;
static Cantor startList(Cantor head, double start_num,
double end_num)
{
if (head == null)
{
head = new Cantor();
head.start = start_num;
head.end = end_num;
head.next = null;
}
return head;
}
static Cantor propagate(Cantor head)
{
Cantor temp = head;
if (temp != null)
{
Cantor newNode = new Cantor();
double diff = (((temp.end) - (temp.start)) / 3);
newNode.end = temp.end;
temp.end = ((temp.start) + diff);
newNode.start = (newNode.end) - diff;
newNode.next = temp.next;
temp.next = newNode;
propagate(temp.next.next);
}
return head;
}
static void print(Cantor temp)
{
while (temp != null)
{
Console.Write("[{0:F6}] -- [{1:F6}]",
temp.start, temp.end);
temp = temp.next;
}
Console.Write("\n");
}
static void buildCantorSet(int A, int B, int L)
{
Cantor head = null;
head = startList(head, A, B);
for (int i = 0; i < L; i++)
{
Console.Write("Level_{0} : ", i);
print(head);
propagate(head);
}
Console.Write("Level_{0} : ", L);
print(head);
}
public static void Main(String[] args)
{
int A = 0;
int B = 9;
int L = 2;
buildCantorSet(A, B, L);
}
}
|
Javascript
<script>
class Cantor
{
constructor()
{
this.start = 0;
this.end = 0;
this.next = null;
}
};
var cantor = null;
function startList(head, start_num, end_num)
{
if (head == null)
{
head = new Cantor();
head.start = start_num;
head.end = end_num;
head.next = null;
}
return head;
}
function propagate(head)
{
var temp = head;
if (temp != null)
{
var newNode = new Cantor();
var diff = (((temp.end) - (temp.start)) / 3);
newNode.end = temp.end;
temp.end = ((temp.start) + diff);
newNode.start = (newNode.end) - diff;
newNode.next = temp.next;
temp.next = newNode;
propagate(temp.next.next);
}
return head;
}
function print(temp)
{
while (temp != null)
{
document.write("["+temp.start.toFixed(6)+"] -- ["+
temp.end.toFixed(6)+"] ");
temp = temp.next;
}
document.write("<br>");
}
function buildCantorSet(A, B, L)
{
var head = null;
head = startList(head, A, B);
for (var i = 0; i < L; i++)
{
document.write("Level_"+ i +" : ");
print(head);
propagate(head);
}
document.write("Level_"+ L +" : ");
print(head);
}
var A = 0;
var B = 9;
var L = 2;
buildCantorSet(A, B, L);
</script>
|
Output:
Level_0 : [0.000000] — [9.000000]
Level_1 : [0.000000] — [3.000000] [6.000000] — [9.000000]
Level_2 : [0.000000] — [1.000000] [2.000000] — [3.000000] [6.000000] — [7.000000] [8.000000] — [9.000000]
References: Cantor Set Wikipedia
Related Article: N-th term of George Cantor set of rational numbers
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...