Temple Offerings
Last Updated :
16 Feb, 2023
Consider a devotee wishing to give offerings to temples along with a mountain range. The temples are located in a row at different heights. Each temple should receive at least one offer. If two adjacent temples are at different altitudes, then the temple that is higher up should receive more offerings than the one that is lower down. If two adjacent temples are at the same height, then their offerings relative to each other do not matter. Given the number of temples and the heights of the temples in order, find the minimum number of offerings to bring.
Examples:
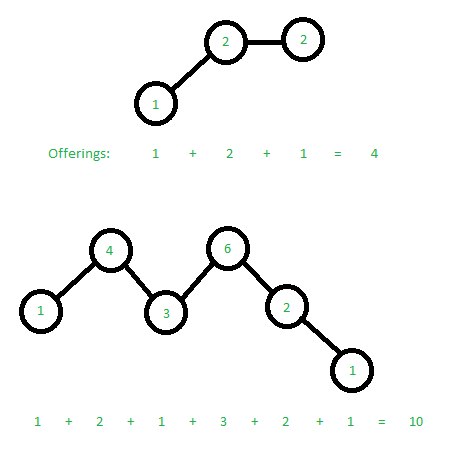
Input : 3
1 2 2
Output : 4
All temples must receive at-least one offering.
Now, the second temple is at a higher altitude
compared to the first one. Thus it receives one
extra offering.
The second temple and third temple are at the
same height, so we do not need to modify the
offerings. Offerings given are therefore: 1, 2,
1 giving a total of 4.
Input : 6
1 4 3 6 2 1
Output : 10
We can distribute the offerings in the following
way, 1, 2, 1, 3, 2, 1. The second temple has to
receive more offerings than the first due to its
height being higher. The fourth must receive more
than the fifth, which in turn must receive more
than the sixth. Thus the total becomes 10.
We notice that each temple can either be above, below or at the same level as the temple next to it. The offerings required at each temple are equal to the maximum length of the chain of temples at a lower height as shown in the image.
Naive Approach:
To follow the given rule, a temple must be offered at least x+1 where x is the maximum of the following two.
- Number of temples on left in increasing order.
- Number of temples on right in increasing order.
A naive method of solving this problem would be for each temple, go to the left until altitude increases, and do the same for the right.
C++
#include <iostream>
using namespace std;
int offeringNumber(int n, int templeHeight[])
{
int sum = 0;
for (int i = 0; i < n; ++i)
{
int left = 0, right = 0;
for (int j = i - 1; j >= 0; --j)
{
if (templeHeight[j] < templeHeight[j + 1])
++left;
else
break;
}
for (int j = i + 1; j < n; ++j)
{
if (templeHeight[j] < templeHeight[j - 1])
++right;
else
break;
}
sum += max(right, left) + 1;
}
return sum;
}
int main()
{
int arr1[3] = {1, 2, 2};
cout << offeringNumber(3, arr1) << "\n";
int arr2[6] = {1, 4, 3, 6, 2, 1};
cout << offeringNumber(6, arr2) << "\n";
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int offeringNumber(int n,
int templeHeight[])
{
int sum = 0;
for (int i = 0; i < n; ++i)
{
int left = 0, right = 0;
for (int j = i - 1; j >= 0; --j)
{
if (templeHeight[j] <
templeHeight[j + 1])
++left;
else
break;
}
for (int j = i + 1; j < n; ++j)
{
if (templeHeight[j] <
templeHeight[j - 1])
++right;
else
break;
}
sum += Math.max(right, left) + 1;
}
return sum;
}
public static void main (String[] args)
{
int arr1[] = {1, 2, 2};
System.out.println(offeringNumber(3, arr1));
int arr2[] = {1, 4, 3,
6, 2, 1};
System.out.println(offeringNumber(6, arr2));
}
}
|
Python3
def offeringNumber(n, templeHeight):
sum = 0
for i in range(n):
left = 0
right = 0
for j in range(i - 1, -1, -1):
if (templeHeight[j] < templeHeight[j + 1]):
left += 1
else:
break
for j in range(i + 1, n):
if (templeHeight[j] < templeHeight[j - 1]):
right += 1
else:
break
sum += max(right, left) + 1
return sum
arr1 = [1, 2, 2]
print(offeringNumber(3, arr1))
arr2 = [1, 4, 3, 6, 2, 1]
print(offeringNumber(6, arr2))
|
C#
using System;
class GFG
{
static int offeringNumber(int n,
int []templeHeight)
{
int sum = 0;
for (int i = 0; i < n; ++i)
{
int left = 0, right = 0;
for (int j = i - 1; j >= 0; --j)
{
if (templeHeight[j] <
templeHeight[j + 1])
++left;
else
break;
}
for (int j = i + 1; j < n; ++j)
{
if (templeHeight[j] <
templeHeight[j - 1])
++right;
else
break;
}
sum += Math.Max(right, left) + 1;
}
return sum;
}
static public void Main ()
{
int []arr1 = {1, 2, 2};
Console.WriteLine(offeringNumber(3, arr1));
int []arr2 = {1, 4, 3,
6, 2, 1};
Console.WriteLine(offeringNumber(6, arr2));
}
}
|
PHP
<?php
function offeringNumber($n, $templeHeight)
{
$sum = 0;
for ($i = 0; $i < $n; ++$i)
{
$left = 0; $right = 0;
for ($j = $i - 1; $j >= 0; --$j)
{
if ($templeHeight[$j] < $templeHeight[$j + 1])
++$left;
else
break;
}
for ($j = $i + 1; $j < $n; ++$j)
{
if ($templeHeight[$j] < $templeHeight[$j - 1])
++$right;
else
break;
}
$sum += max($right, $left) + 1;
}
return $sum;
}
$arr1 = array (1, 2, 2);
echo offeringNumber(3, $arr1) , "\n";
$arr2 = array (1, 4, 3, 6, 2, 1);
echo offeringNumber(6, $arr2) ,"\n";
?>
|
Javascript
<script>
function offeringNumber(n, templeHeight)
{
let sum = 0;
for (let i = 0; i < n; ++i)
{
let left = 0, right = 0;
for (let j = i - 1; j >= 0; --j)
{
if (templeHeight[j] < templeHeight[j + 1])
++left;
else
break;
}
for (let j = i + 1; j < n; ++j)
{
if (templeHeight[j] < templeHeight[j - 1])
++right;
else
break;
}
sum += Math.max(right, left) + 1;
}
return sum;
}
let arr1 = [1, 2, 2];
document.write(offeringNumber(3, arr1) + "</br>");
let arr2 = [1, 4, 3, 6, 2, 1];
document.write(offeringNumber(6, arr2));
</script>
|
Time Complexity: O(n2)
Auxiliary Space: O(1)
Dynamic Programming Approach:
By using Dynamic Programming, we can improve the time complexity. In this method, we create a structure of length n which maintains the maximum decreasing chain to the left of each temple and the maximum decreasing chain to the right of each temple. We go through once from 0 to N setting the value of left for each temple. We then go from N to 0 setting the value of right for each temple. We then compare the two and pick the maximum for each temple.
C++
#include <iostream>
using namespace std;
struct Temple {
int L;
int R;
};
int offeringNumber(int n, int templeHeight[])
{
Temple chainSize[n];
for (int i = 0; i < n; ++i) {
chainSize[i].L = -1;
chainSize[i].R = -1;
}
chainSize[0].L = 1;
chainSize[n - 1].R = 1;
for (int i = 1; i < n; ++i) {
if (templeHeight[i - 1] < templeHeight[i])
chainSize[i].L = chainSize[i - 1].L + 1;
else
chainSize[i].L = 1;
}
for (int i = n - 2; i >= 0; --i) {
if (templeHeight[i + 1] < templeHeight[i])
chainSize[i].R = chainSize[i + 1].R + 1;
else
chainSize[i].R = 1;
}
int sum = 0;
for (int i = 0; i < n; ++i)
sum += max(chainSize[i].L, chainSize[i].R);
return sum;
}
int main()
{
int arr1[3] = { 1, 2, 2 };
cout << offeringNumber(3, arr1) << "\n";
int arr2[6] = { 1, 4, 3, 6, 2, 1 };
cout << offeringNumber(6, arr2) << "\n";
return 0;
}
|
Java
import java.util.*;
class GFG {
public static class Temple {
public int L;
public int R;
};
static int offeringNumber(int n, int[] templeHeight)
{
Temple[] chainSize = new Temple[n];
for (int i = 0; i < n; ++i) {
chainSize[i] = new Temple();
chainSize[i].L = -1;
chainSize[i].R = -1;
}
chainSize[0].L = 1;
chainSize[n - 1].R = 1;
for (int i = 1; i < n; ++i) {
if (templeHeight[i - 1] < templeHeight[i])
chainSize[i].L = chainSize[i - 1].L + 1;
else
chainSize[i].L = 1;
}
for (int i = n - 2; i >= 0; --i) {
if (templeHeight[i + 1] < templeHeight[i])
chainSize[i].R = chainSize[i + 1].R + 1;
else
chainSize[i].R = 1;
}
int sum = 0;
for (int i = 0; i < n; ++i)
sum += Math.max(chainSize[i].L, chainSize[i].R);
return sum;
}
public static void main(String[] s)
{
int[] arr1 = { 1, 2, 2 };
System.out.println(offeringNumber(3, arr1));
int[] arr2 = { 1, 4, 3, 6, 2, 1 };
System.out.println(offeringNumber(6, arr2));
}
}
|
Python3
from typing import List
class Temple:
def __init__(self, l: int, r: int):
self.L = l
self.R = r
def offeringNumber(n: int,
templeHeight: List[int]) -> int:
chainSize = [0] * n
for i in range(n):
chainSize[i] = Temple(-1, -1)
chainSize[0].L = 1
chainSize[-1].R = 1
for i in range(1, n):
if templeHeight[i - 1] < templeHeight[i]:
chainSize[i].L = chainSize[i - 1].L + 1
else:
chainSize[i].L = 1
for i in range(n - 2, -1, -1):
if templeHeight[i + 1] < templeHeight[i]:
chainSize[i].R = chainSize[i + 1].R + 1
else:
chainSize[i].R = 1
sm = 0
for i in range(n):
sm += max(chainSize[i].L,
chainSize[i].R)
return sm
if __name__ == '__main__':
arr1 = [1, 2, 2]
print(offeringNumber(3, arr1))
arr2 = [1, 4, 3, 6, 2, 1]
print(offeringNumber(6, arr2))
|
C#
using System;
class GFG {
public class Temple {
public int L;
public int R;
};
static int offeringNumber(int n, int[] templeHeight)
{
Temple[] chainSize = new Temple[n];
for (int i = 0; i < n; ++i) {
chainSize[i] = new Temple();
chainSize[i].L = -1;
chainSize[i].R = -1;
}
chainSize[0].L = 1;
chainSize[n - 1].R = 1;
for (int i = 1; i < n; ++i) {
if (templeHeight[i - 1] < templeHeight[i])
chainSize[i].L = chainSize[i - 1].L + 1;
else
chainSize[i].L = 1;
}
for (int i = n - 2; i >= 0; --i) {
if (templeHeight[i + 1] < templeHeight[i])
chainSize[i].R = chainSize[i + 1].R + 1;
else
chainSize[i].R = 1;
}
int sum = 0;
for (int i = 0; i < n; ++i)
sum += Math.Max(chainSize[i].L, chainSize[i].R);
return sum;
}
static void Main()
{
int[] arr1 = { 1, 2, 2 };
Console.Write(offeringNumber(3, arr1) + "\n");
int[] arr2 = { 1, 4, 3, 6, 2, 1 };
Console.Write(offeringNumber(6, arr2) + "\n");
}
}
|
Javascript
const offeringNumber = (n, templeHeight) => {
let chainSize = new Array(n);
for (let i = 0; i < n; ++i) {
chainSize[i] = { L: -1, R: -1 };
}
chainSize[0].L = 1;
chainSize[n - 1].R = 1;
for (let i = 1; i < n; ++i) {
if (templeHeight[i - 1] < templeHeight[i])
chainSize[i].L = chainSize[i - 1].L + 1;
else
chainSize[i].L = 1;
}
for (let i = n - 2; i >= 0; --i) {
if (templeHeight[i + 1] < templeHeight[i])
chainSize[i].R = chainSize[i + 1].R + 1;
else
chainSize[i].R = 1;
}
let sum = 0;
for (let i = 0; i < n; ++i)
sum += Math.max(chainSize[i].L, chainSize[i].R);
return sum;
}
let arr = [1,2,2]
console.log(offeringNumber(3, arr));
let arr1=[1, 4, 3, 6, 2, 1]
console.log(offeringNumber(6, arr1));
|
Time Complexity: O(n)
Auxiliary Space: O(n)
Greedy Approach:
If we somehow manage to make sure that the temple at higher mountain is getting more offerings then our problem is solved. For this we can make use of greedy (since we have to compare only the neighbors of current index). The approach is to do two traversals (in two directions), first one to make sure that the temple gets more offerings than the left temple (at higher position) and second one to make sure that the temple at higher position from the right gets more offerings.
C++
#include <iostream>
using namespace std;
int templeOfferings(int nums[], int n)
{
int offerings[n];
offerings[0] = 1;
for (int i = 1; i < n; i++)
{
if (nums[i] > nums[i - 1])
offerings[i] = offerings[i - 1] + 1;
else
offerings[i] = 1;
}
for (int i = n - 2; i >= 0; i--)
{
if (nums[i] > nums[i + 1] && offerings[i] <= offerings[i + 1])
offerings[i] = offerings[i + 1] + 1;
}
int sum = 0;
for (int val : offerings)
sum += val;
return sum;
}
int main()
{
int arr[] = { 1, 4, 3, 6, 2, 1 };
int n = sizeof(arr)/sizeof(arr[0]);
cout << (templeOfferings(arr, n));
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int[] arr = { 1, 4, 3, 6, 2, 1 };
int n = arr.length;
System.out.println(templeOfferings(arr, n));
}
private static int templeOfferings(int[] nums, int n)
{
int[] offerings = new int[n];
offerings[0] = 1;
for (int i = 1; i < n; i++) {
if (nums[i] > nums[i - 1])
offerings[i] = offerings[i - 1] + 1;
else
offerings[i] = 1;
}
for (int i = n - 2; i >= 0; i--) {
if (nums[i] > nums[i + 1]
&& offerings[i] <= offerings[i + 1])
offerings[i] = offerings[i + 1] + 1;
}
int sum = 0;
for (int val : offerings)
sum += val;
return sum;
}
}
|
Javascript
function templeOfferings( nums, n)
{
let offerings=new Array(n);
offerings[0] = 1;
for (let i = 1; i < n; i++)
{
if (nums[i] > nums[i - 1])
offerings[i] = offerings[i - 1] + 1;
else
offerings[i] = 1;
}
for (let i = n - 2; i >= 0; i--)
{
if (nums[i] > nums[i + 1] && offerings[i] <= offerings[i + 1])
offerings[i] = offerings[i + 1] + 1;
}
let sum = 0;
for (let val of offerings)
sum += val;
return sum;
}
let arr = [ 1, 4, 3, 6, 2, 1 ];
let n = arr.length;
console.log(templeOfferings(arr, n));
|
C#
using System;
using System.Linq;
using System.Collections.Generic;
class GFG
{
static int templeOfferings(int[] nums, int n)
{
int[] offerings=new int[n];
offerings[0] = 1;
for (int i = 1; i < n; i++)
{
if (nums[i] > nums[i - 1])
offerings[i] = offerings[i - 1] + 1;
else
offerings[i] = 1;
}
for (int i = n - 2; i >= 0; i--)
{
if (nums[i] > nums[i + 1] && offerings[i] <= offerings[i + 1])
offerings[i] = offerings[i + 1] + 1;
}
int sum = 0;
foreach (int val in offerings)
sum += val;
return sum;
}
static public void Main()
{
int[] arr = { 1, 4, 3, 6, 2, 1 };
int n = arr.Length;
Console.Write(templeOfferings(arr, n));
}
}
|
Python3
def templeOfferings(nums, n):
offerings = [0] * n
offerings[0] = 1
for i in range(1, n):
if nums[i] > nums[i - 1]:
offerings[i] = offerings[i - 1] + 1
else:
offerings[i] = 1
for i in range(n - 2, -1, -1):
if nums[i] > nums[i + 1] and offerings[i] <= offerings[i + 1]:
offerings[i] = offerings[i + 1] + 1
return sum(offerings)
if __name__ == "__main__":
arr = [1, 4, 3, 6, 2, 1]
n = len(arr)
print(templeOfferings(arr, n))
|
Time Complexity: O(n)
Auxiliary Space: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...