Tangent and Normals are the lines that are used to define various properties of the curves. We define tangent as the line which touches the circle only at one point and normal is the line that is perpendicular to the tangent at the point of tangency. Any tangent of the curve passing through the point (x1, y1) is of the form y – y1 = m(x-x1) and the equation of the normal at that point is represented using y – y1 = -1/m(x-x1) where m is the slope of the line.
Tangents and normals are lines related to curves. A tangent is a line that touches a curve at a specific point without crossing it at that point, and every point on a curve has its tangent. A normal, on the other hand, is a line that is perpendicular to the tangent at the point where the tangent contacts the curve.
Let us learn more about the equation of tangents and normals for various curves like circles, parabolas, and other curves, examples, and others in this article.
What are Tangents and Normals?
Tangents and Normals are the lines that we associate with any curve that help us to study and solve various problems of the curves. A line that touches the curve at only one point is the tangent of the curve and any line perpendicular to the curve at the point of tangency is the normal to that curve at that point.
We can draw various tangents to the curve which touches the curve at only one point and the normal can be drawn to the curve at that point. As tangent and normal are straight lines so we represent them using the equation of the straight line. We can easily draw tangent and normal to all types of the curve such as Circles, Ellipses, Parabolas, Hyperbolas, and others. Now let’s learn about Tangent and normal in detail.
What are Tangents?
Tangent is a line that touches a curve at a particular point externally. At a given point of a curve, one and only one tangent passes through it. For a given curve tangent at a particular point is a straight line that just touches that curve at that point, and it goes in the same direction as the curve at that point. We can assume tangent as a line that touches the circle only once. For example, If we take a stone tied to a rope and rotate the stone then at any point if we stop rotating the stone then it goes in a straight line, which is called the tangent to the line at that point.
Tangent Definition
A tangent is a line or plane that touches a curve or curved surface at exactly one point and does not intersect it at or near that point. This line or plane is said to be “tangent” to the curve at that specific point.
For any curve, F(x) the tangent at point (x1, y1) is defined at the line, y – y1 = m(x-x1) where m is the slope of the line.

Tangents and Normals
Properties of Tangents
The tangent to a curve has various properties and some of them are,
- Tangents touch the curve only at one point.
- If any tangent to a curve y = f(x) makes angle θ with the x-axis, then dy/dx = Slope of Tangent = tan θ.
- If the slope of the tangent is zero, then tan θ will be equal to 0 and so θ = 0 which implies that the tangent line is parallel to the x-axis.
- If the slope of the tangent is (θ) = π/2, then tan θ will approach ∞, i.e., the tangent line is perpendicular to the x-axis.
What are Normal?
Normal to the curve at any given point is defined as the line passing through the curve which is perpendicular to the tangent of the curve at the point of tangency.
Normal Definition
Normal refers to a line that is perpendicular to the tangent line at the point of tangency on the curve. This perpendicular line extends in both directions from the point where it meets the curve.
For any curve, F(x) the equation of normal at point (x1, y1) is defined at the line, y – y1 = -1/m(x-x1) where m is the slope of the tangent line passing through that point.

Tangents and Normals
Properties of Normals
The normal line to the curve has various properties and some of them are,
- A normal line at any point of a circle will always pass through the center of the circle.
- The normal to any curve is always perpendicular to the tangent at any point on the curve.
How To Find Tangents and Normals?
To find the Tangents and Normals to a curve we require the equation of the curve and the point at which we have to find the tangent and normal. Suppose the point at which we require to find the equation of the Tangents and Normals to the curve is (x1, y1) and the equation of the curve is f(x) then we can easily find the equation of the tangent and normal to the curve.
We know that the tangents and the normal are perpendicular to each other and the slope of the curve y = f(x) at any point (x1, y1) is given using the formula,
m = (dy/dx) at (x1, y1)
We also know that if the slope of the tangent line is m1 and the slope of the perpendicular line is m2 then,
m1 × m2 = -1
Using these we can easily find the tangent and normal to any curve of the circle.
Equation of Tangent and Normal to the Curve
We can calculate the equation of tangent and normal of the curve by various means that include.
- In Cartesian Coordinates System
- In Parametric Form
In Cartesian Coordinates System
At a point on the curve, the gradient of the curve is equal to the gradient of the tangent to the curve at that point. So, the equation of a tangent can be found by the gradient at that point to the curve and the given point as follows,
As we know that the equation of the straight line passes through point P (x0, y0) is
y – y0 = m(x – x0)
Here, m is the finite slope of the line. Now the slope of the tangent to a curve given is y = f(x) at point P (x0, y0) is f'(x0). Then the equation of the tangent to the curve at point P(x0, y0) is
y – y0 = f'(x0)(x – x0)
For the normal, as we already know that the normal is always perpendicular to the tangent line. Then the slope of the normal to the curve will be:
Slope of Normal = -1/f'(x0)
So, the equation of normal to the curve y = f(x) at the point (x0, y0) is,
y – y0 = [-1/f'(x0)](x – x0)
f'(x0)(y – y0) + (x – x0) = 0
In Parametric Form
Let us assume the parametric form of the curve is
x = x(t) ….(i)
y = y(t) ….(ii)
Now we find the slope of the tangent to a curve at the point (x0, y0), by using the differentiation rule:
m = tan α = y'(t)/x'(t)
Hence, the equation of the tangent is:
y – y0 = [y'(t)/x'(t)](x – x0)
Accordingly, the equation of the normal is:
y – y0 = – x'(t)/y'(t)(x – x0)
y'(t)(y – y0) + x'(t)(x – x0) = 0
Tangents and Normals for Various Curves
We can easily find the tangent and normal to various curves and some of the important curves and the equation of their tangent and normal are,
Circle: For the circle represented using the equation x2 + y2 + 2gx + 2fy + c = 0 and at the point (x1, y1). The equations for Tangent and Normal for the circle are given as,
Tangent: xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
Normal: (y – y1)/(y1 + f) = (x – x1)/(x1 + g)
Parabola: For the parabola represented using the equation y2 = 4ax, and at the point (x1, y1). The equations for Tangent and Normal for parabola are given as,
Tangent: yy1 = 2a(x + x1)
Normal: (y-y1) = (-y1/2a)(x – x1)
Ellipse: For the ellipse represented using the equation x2/a2 + y2/b2 = 1, and at the point (x1, y1). The equations for Tangent and Normal for ellipse are given as,
Tangent: xx1/a2 + yy1/b2 = 1
Normal: a2x/x1 – b2y/y1 = a2 – b2
Hyperbola: For the hyperbola represented using the equation x2/a2 – y2/b2 = 1, and at the point (x1, y1). The equations for Tangent and Normal for hyperbola are given as,
Tangent: xx1/a2 – yy1/b2 = 1
Normal: (y – y1) = (-a2y1/b2x1)(x – x1)
Similarly the equation of the normal at the point (x1, y1), for each of the above-given curves, can be calculated by taking the negative of the inverse differentiation of the curve at the given point, as the slope of the curve and then forming the equation of the normal using the formula for the equation of the line passing through the given point and having slope m.
People Also Read:
Practice Problems on Tangents and Normals
1. Find the equation of the tangent line to the curve f(x) = x2 at x = 3.
2. Find the equation of the normal line to the curve g(x) = 3x3 at x = 1.
3. If h(x) = x1/2, calculate the slope of the tangent and the normal at x = 4.
4. Determine the points on the curve y = x2 – 4x + 4 where the tangent is horizontal.
5. Find the equations of both the tangent and the normal to the curve y = x3 – 6x2 + 11x – 6 at x = 2.
Tangents And Normals Examples
Example 1: Find the slope of the tangent and the normal to the curve y = 6x2 – 10x at x = 1.
Solution:
Given Curve y = 6x2 – 10x
dy/dx = 12x − 10
Slope of tangent to the given curve at x = 1 is,
m1 = [dy/dx]x=1 = 12 × 1 – 10 = 2
We know that,
Slope of Tangent × Slope of Normal = m1 × m2 = -1
Slope of Normal = -1/2 = -0.5
Example 2: Find The slope of the tangent and normal to the curve y = 3x3 + 3sin(x) at x = 0.
Solution:
The given curve is y = 3x3 + 3sin(x)
Now the gradient, dy/dx = 9x2 + 3cos(x)
So, the slope of the tangent to the given curve at x = 0 is,
dy/dx]x=0 = 0 + 3 × 1 = 3
The slope of the normal will be:
= -1/3
Example 3: Find the equation of the tangent to the curve y = 6x2 – 2x + 3 at P(1, 0).
Solution:
The given curve is y = 6x2 – 2x + 3
Now the gradient, dy/dx = 12x – 2
So, the slope of the tangent to the given curve at P(1,0) is
dy/dx]1,0 = 12 – 2 = 10
The equation of the tangent will be:
y – 0 = 10(x – 1)
y = 10x – 10
Example 4: Determine the point on the curve y = 6x2 – 8x + 1 where the tangent is parallel to the line y = 4x – 5.
Solution:
Given curve is y = 6x2 – 8x + 1
Now the gradient, dy/dx = 12x – 8
Tangent is parallel to y = 4x – 5
so,
12x0 – 8 = 4
or x0 = 1
Putting x = 1 in equation of the curve
We get,
y0 = 6 – 8 + 1
y0 = -1
So the point is (1, -1)
Example 5: Find the slope of the tangent to the curve given by:
x = psin3u, y = qcos3u at point where u = π/2.
Solution:
Given,
x = psin3u …(i)
y = qcos3u …(ii)
Value of u = π/2
On differentiating eq(i) and (ii), w.r.t u, we get
dx/du = 3psin2u.cosu …(iii)
dy/du = -3qcos2u.sinu …(iv)
Now we find the slope of the tangent at point u = π/2
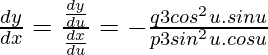
dy/dx = -qcosu/psinu
[dy/dx]u=π/2 = -qcos(π/2)/psin(π/2) = 0
Hence, slope of tangent is m = 0
FAQs on Tangents And Normals
What are Tangents?
We define tanget as the curve which touches the curve at only one point and that point is called the point of tangency.
What are Normals?
The normals are the line which are perpendicular to the tangent and are drawn at the point ogf tangency.
How to find Tangents and Normals?
To find tangent and normal we require the point (say x1, y1) on the curve at which the tangent is required and then we find the differentiation of the curve at that point which gives the slope of the tangent at that point, (say m). Now if the slope of the line m and the point at which the line passes (x1, y1) is given then we find the equation of the tangent by,
y – y1 = m(x – x1)
For the equation of normal, we take its slope as -1/m then find the equation of the line using the above formula.
What is the Equation of Tangents and Normals?
If the point on the curve is (x1, y1) and the slope of the tangent is m, and the slope of the normal is -1/m, then the equation of the tangent is,
y – y1 = m(x – x1)
And, the equation of normal is,
y – y1 = -1/m(x – x1)
How many Tangents are in a Circle?
We can draw infinite tangents to circle. But, we have to note that from a particular point outside the circle, we can draw only two tangents to a circle.
When is the Tangent Parallel to the Y-axis?
If the tangent of any curve at the given point is of the form,
x = h
where h is any constant. Then we say that the tangent is parallel to the y-axis.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...