Syntactically analysis in Artificial Intelligence
Last Updated :
21 Apr, 2022
In this article, we are going to see about syntactically analysing in Artificial Intelligence.
Parsing is the process of studying a string of words in order to determine its phrase structure using grammatical rules. We can start with the S sign and search top-down for a tree with the words as its leaves, or we can start with the words and search bottom up for a tree that ends in an S, as shown in Figure 23.4. Top-down and bottom-up parsing, on the other hand, can be wasteful since they might result in the same amount of effort being used on parts of the search space that lead to dead ends.
Take a look at the following two sentences:
- Have students in the Physics class take the test?
- Have students in the Physics class taken the test?
These phrases have completely distinct parses, despite the fact that they share the first ten words. The first is a command, while the second is a query. A left-to-right parsing algorithm would have to estimate whether the first word is part of a command or a question, and won’t know if it’s right until the eleventh word, take or taken. If the algorithm is incorrect, it will have to go back to the initial word and re-analyze the entire phrase using the other meaning.
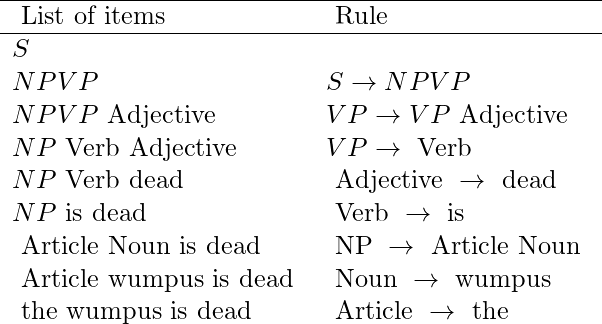
We can utilize dynamic programming to eliminate this source of inefficiency: every time we examine a substring, save the findings so we don’t have to reanalyze them later. For example, after we determine that “the students in the Physics class” is an NP, we may store the information in a data structure called a chart. Chart parsers are algorithms that achieve this. Because we’re working with context-free grammar, every term found in one branch of the search space can be used in any other branch. There are many other types of chart parsers; we discuss the CYK method, which is named after its creators, John Cocke, Daniel Younger, and Tadeo Kasami.
It’s worth noting that the CYK algorithm necessitates a grammar that contains all rules in one of two very particular formats: lexical rules in the form  , and syntactic rules in the form
, and syntactic rules in the form 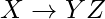 . This grammatical type, known as Chomsky Normal Form, may appear to be limited, but it is not: any context-free grammar may be turned into Chomsky Normal Form automatically.
. This grammatical type, known as Chomsky Normal Form, may appear to be limited, but it is not: any context-free grammar may be turned into Chomsky Normal Form automatically.
For general context-free grammars, no algorithm can beat the CYK algorithm, though there are faster algorithms for more restricted grammars. Given that a phrase might have an exponential number of parse trees, the method completing in O(n3) time is quite a feat. Consider the sentence
Fall leaves fall and spring leaves spring.
It’s unclear since each word (save “and”) can be a noun or a verb, and “fall” and “spring” can also be adjectives. (For instance, one interpretation of “Fall departs fall” is “Autumn abandons autumn.”) [S [S [NP Fall leaves] fall] and [S [NP Spring leaves] spring] are two of the four parses in  .
.
We would have 2c possibilities of choosing parses for the subsentences if we had c two-way-ambiguous conjoined subsentences. In O(c3) time, how does the CYK algorithm handle these 2c parse trees? The solution is that it doesn’t need to look at all of the parse trees; all it needs to do is compute the probability of the most likely one. The subtrees are all represented in the P table, and we could enumerate them all (in exponential time) with a little effort, but the beauty of the CYK method is that we don’t have to.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...