Super-Poulet Number
Last Updated :
27 Sep, 2022
Super-Poulet number is a Poulet number (pseudoprime) to base 2 if each and every divisor D divides 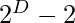 .
.
Some of the super-poulet numbers are:
341, 1387, 2047, 2701, 3277, 4033….
Check if N is a Super-poulet number
Given an integer N, the task is to check N is a Super-Poulet Number.
Examples:
Input: N = 341
Output: Yes
Input: N = 10
Output: No
Approach: The idea is to generate all the divisors of the number N and for all divisor check D divides 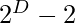 . If this condition satisfy for all divisors then the number is super-poulet number.
. If this condition satisfy for all divisors then the number is super-poulet number.
For Example:
For N = 341,
Divisors of 341 are {1, 11, 31, 341} and,
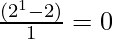
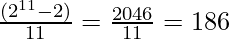
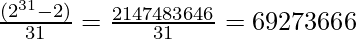
Similarly, 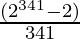 also gives integer value.
also gives integer value.
Therefore, 341 is a super-poulet number.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> findDivisors(int n)
{
vector<int> divisors;
for (int i = 1; i < (sqrt(n) + 1); i++) {
if (n % i == 0) {
if (n / i == i)
divisors.push_back(i);
else {
divisors.push_back(i);
divisors.push_back((n / i));
}
}
}
sort(divisors.begin(), divisors.end());
return divisors;
}
bool isSuperdNum(int n)
{
vector<int> d = findDivisors(n);
for (int i : d) {
double x = (pow(2, i) - 2) / i;
if (floor(x) != x)
return false;
}
return true;
}
int main()
{
int n = 341;
if (isSuperdNum(n) == true)
cout << "Yes";
else
cout << "No";
}
|
Java
import java.util.*;
class GFG
{
static ArrayList<Integer> findDivisors(int n)
{
ArrayList<Integer> divisors = new ArrayList<Integer>();
for (int i = 1; i < (Math.sqrt(n) + 1); i++)
{
if (n % i == 0)
{
if (n / i == i)
divisors.add(i);
else
{
divisors.add(i);
divisors.add((n / i));
}
}
}
Collections.sort(divisors);
return divisors;
}
static boolean isSuperdNum(int n)
{
ArrayList<Integer> d = findDivisors(n);
for(int i : d)
{
double x = (Math.pow(2, i) - 2) / i;
if (Math.floor(x) != x)
return false;
}
return true;
}
public static void main(String[] args)
{
int n = 341;
if (isSuperdNum(n) == true)
System.out.print("Yes");
else
System.out.print("No");
}
}
|
Python3
import math
def findDivisors(n):
divisors = []
for i in range(1,\
int(math.sqrt(n) + 1)):
if (n % i == 0) :
if (n / i == i):
divisors.append(i)
else:
divisors.append(i)
divisors.append(int(n / i))
return sorted(divisors)
def isSuperdNum(n):
d = findDivisors(n)
for i in d:
x = (2**i-2)/i
if int(x) != x:
return False
return True
if __name__ == "__main__":
n = 341
if isSuperdNum(n) == True:
print("Yes")
else :
print("No")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static List<int> findDivisors(int n)
{
List<int> divisors = new List<int>();
for (int i = 1; i < (Math.Sqrt(n) + 1); i++)
{
if (n % i == 0)
{
if (n / i == i)
divisors.Add(i);
else
{
divisors.Add(i);
divisors.Add((n / i));
}
}
}
divisors.Sort();
return divisors;
}
static bool isSuperdNum(int n)
{
List<int> d = findDivisors(n);
foreach(int i in d)
{
double x = (Math.Pow(2, i) - 2) / i;
if (Math.Truncate(x) != x)
return false;
}
return true;
}
public static void Main(string[] args)
{
int n = 341;
if (isSuperdNum(n) == true)
Console.Write("Yes");
else
Console.Write("No");
}
}
|
Javascript
<script>
function findDivisors(n){
let divisors = []
for(let i = 1; i < Math.floor(Math.sqrt(n) + 1); i++){
if (n % i == 0) {
if (n / i == i){
divisors.push(i)
}
else{
divisors.push(i)
divisors.push(Math.floor(n / i))
}
}
}
return divisors.sort((a, b)=> a - b)
}
function isSuperdNum(n){
let d = findDivisors(n)
for(let i in d){
let x = (2**i - 2) / i
if (Math.floor(x) != x){
return false
}
}
return true
}
let n = 341
if(isSuperdNum(n) == true){
document.write("Yes")
}
else {
document.write("No")
}
</script>
|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...