Sum of squares of binomial coefficients

Given a positive integer n. The task is to find the sum of square of Binomial Coefficient i.e 
ⁿC₀² + ⁿC₁² + ⁿC₂² + ⁿC₃² + ……… + ⁿC_n-2² + ⁿC_n-1² + ⁿC_n²
Examples:

Input : n = 4
Output : 70

Input : n = 5
Output : 252

Method 1: (Brute Force)
The idea is to generate all the terms of binomial coefficient and find the sum of square of each binomial coefficient.
Below is the implementation of this approach:

C++

// CPP Program to find the sum of square of
// binomial coefficient.
#include<bits/stdc++.h>
using namespace std;

// Return the sum of square of binomial coefficient
int sumofsquare(int n)
{
    int C[n+1][n+1];
    int i, j;

    // Calculate value of Binomial Coefficient
    // in bottom up manner
    for (i = 0; i <= n; i++)
    {
        for (j = 0; j <= min(i, n); j++)
        {
            // Base Cases
            if (j == 0 || j == i)
                C[i][j] = 1;

            // Calculate value using previously
            // stored values
            else
                C[i][j] = C[i-1][j-1] + C[i-1][j];
        }
    }

    // Finding the sum of square of binomial
    // coefficient.
    int sum = 0;
    for (int i = 0; i <= n; i++)
        sum += (C[n][i] * C[n][i]);

    return sum;
}

// Driven Program
int main()
{
    int n = 4;
    cout << sumofsquare(n) << endl;
    return 0;
}

Java

// Java Program to find the sum of
// square of binomial coefficient.
import static java.lang.Math.*;

class GFG{

    // Return the sum of square of
    // binomial coefficient
    static int sumofsquare(int n)
    {
        int[][] C = new int [n+1][n+1] ;
        int i, j;

        // Calculate value of Binomial
        // Coefficient in bottom up manner
        for (i = 0; i <= n; i++)
        {
            for (j = 0; j <= min(i, n); j++)
            {
                // Base Cases
                if (j == 0 || j == i)
                    C[i][j] = 1;

                // Calculate value using
                //previously stored values
                else
                    C[i][j] = C[i-1][j-1]
                             + C[i-1][j];
            }
        }

        // Finding the sum of square of
        // binomial coefficient.
        int sum = 0;
        for (i = 0; i <= n; i++)
            sum += (C[n][i] * C[n][i]);

        return sum;
    }

    // Driver function
    public static void main(String[] args)
    {
        int n = 4;

        System.out.println(sumofsquare(n));
    }
}

// This code is contributed by
// Smitha Dinesh Semwal

Python3

# Python Program to find
# the sum of square of
# binomial coefficient.

# Return the sum of
# square of binomial
# coefficient
def sumofsquare(n) :

    C = [[0 for i in range(n + 1)]
            for j in range(n + 1)]

    # Calculate value of
    # Binomial Coefficient
    # in bottom up manner
    for i in range(0, n + 1) :

        for j in range(0, min(i, n) + 1) :

            # Base Cases
            if (j == 0 or j == i) :
                C[i][j] = 1

            # Calculate value
            # using previously
            # stored values
            else :
                C[i][j] = (C[i - 1][j - 1] +
                           C[i - 1][j])


    # Finding the sum of
    # square of binomial
    # coefficient.
    sum = 0
    for i in range(0, n + 1) :
        sum = sum + (C[n][i] *
                     C[n][i])

    return sum


# Driver Code
n = 4
print (sumofsquare(n), end="\n")

# This code is contributed by
# Manish Shaw(manishshaw1)

C#

// C# Program to find the sum of
// square of binomial coefficient.
using System;

class GFG {

    // Return the sum of square of
    // binomial coefficient
    static int sumofsquare(int n)
    {
        int[,] C = new int [n+1,n+1] ;
        int i, j;

        // Calculate value of Binomial
        // Coefficient in bottom up manner
        for (i = 0; i <= n; i++)
        {
            for (j = 0; j <= Math.Min(i, n); j++)
            {
                // Base Cases
                if (j == 0 || j == i)
                    C[i,j] = 1;

                // Calculate value using
                //previously stored values
                else
                    C[i,j] = C[i-1,j-1]
                            + C[i-1,j];
            }
        }

        // Finding the sum of square of
        // binomial coefficient.
        int sum = 0;
        for (i = 0; i <= n; i++)
            sum += (C[n,i] * C[n,i]);

        return sum;
    }

    // Driver function
    public static void Main()
    {
        int n = 4;

        Console.WriteLine(sumofsquare(n));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// PHP Program to find the sum of
// square of binomial coefficient.

// Return the sum of square of binomial
// coefficient
function sumofsquare($n)
{
    $i; $j;

    // Calculate value of Binomial
    // Coefficient in bottom up manner
    for ($i = 0; $i <= $n; $i++)
    {
        for ($j = 0; $j <= min($i, $n); $j++)
        {

            // Base Cases
            if ($j == 0 || $j == $i)
                $C[$i][$j] = 1;

            // Calculate value using previously
            // stored values
            else
                $C[$i][$j] = $C[$i-1][$j-1]
                                + $C[$i-1][$j];
        }
    }

    // Finding the sum of square of binomial
    // coefficient.
    $sum = 0;
    for ($i = 0; $i <= $n; $i++)
        $sum += ($C[$n][$i] * $C[$n][$i]);

    return $sum;
}

// Driven Program
    $n = 4;
    echo sumofsquare($n), "\n";

// This code is contributed by ajit
?>

Javascript

<script>

// JavaScript Program to find the sum of
// square of binomial coefficient.

    // Return the sum of square of
    // binomial coefficient
    function sumofsquare(n)
    {
        let  C = new Array(n+1);

        // Loop to create 2D array using 1D array
        for (let i = 0; i < C.length; i++) {
            C[i] = new Array(2);
        }

        let  i, j;

        // Calculate value of Binomial
        // Coefficient in bottom up manner
        for (i = 0; i <= n; i++)
        {
            for (j = 0; j <= Math.min(i, n); j++)
            {

                // Base Cases
                if (j == 0 || j == i)
                    C[i][j] = 1;

                // Calculate value using
                //previously stored values
                else
                    C[i][j] = C[i-1][j-1]
                             + C[i-1][j];
            }
        }

        // Finding the sum of square of
        // binomial coefficient.
        let sum = 0;
        for (i = 0; i <= n; i++)
            sum += (C[n][i] * C[n][i]);

        return sum;
    }

// Driver code
        let  n = 4;
        document.write(sumofsquare(n));

       // This code is contributed by code_hunt.
</script>

Output:

70

Time Complexity: O(n²)
Space Complexity: O(n²)

Method 2: (Using Formula)

= 
= 
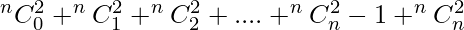
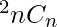
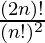
Proof, 

We know,
(1 + x)n = nC0 + nC1 x + nC2 x2 + ......... + nCn-1 xn-1 + nCn-1 xn
Also,
(x + 1)n = nC0 xn + nC1 xn-1 + nC2 xn-2 + ......... + nCn-1 x + nCn

Multiplying above two equations,
(1 + x)2n = [nC0 + nC1 x + nC2 x2 + ......... + nCn-1 xn-1 + nCn-1 xn] X 
            [nC0 xn + nC1 xn-1 + nC2 xn-2 + ......... + nCn-1 x + nCn]

Equating coefficients of xn on both sides, we get
2nCn = nC02 + nC12 + nC22 + nC32 + ......... + nCn-22 + nCn-12 + nCn2

Hence, sum of the squares of coefficients = 2nCn = (2n)!/(n!)2.

Also, (2n)!/(n!)² = (2n * (2n – 1) * (2n – 2) * ….. * (n+1))/(n * (n – 1) * (n – 2) *….. * 1).
Below is the implementation of this approach: 

C++

// CPP Program to find the sum of square of
// binomial coefficient.
#include<bits/stdc++.h>
using namespace std;

// function to return product of number
// from start to end.
int factorial(int start, int end)
{
    int res = 1;
    for (int i = start; i <= end; i++)
        res *= i;

    return res;
}

// Return the sum of square of binomial
// coefficient
int sumofsquare(int n)
{
    return factorial(n+1, 2*n)/factorial(1, n);
}

// Driven Program
int main()
{
    int n = 4;
    cout << sumofsquare(n) << endl;
    return 0;
}

Java

// Java Program to find the sum of square of
// binomial coefficient.
class GFG{

    // function to return product of number
    // from start to end.
    static int factorial(int start, int end)
    {
        int res = 1;
        for (int i = start; i <= end; i++)
            res *= i;

        return res;
    }

    // Return the sum of square of binomial
    // coefficient
    static int sumofsquare(int n)
    {
        return factorial(n+1, 2*n)/factorial(1, n);
    }

    // Driven Program
    public static void main(String[] args)
    {
        int n = 4;
        System.out.println(sumofsquare(n));
    }
}

// This code is contributed by
// Smitha DInesh Semwal

Python

# Python 3 Program to find the sum of
# square of binomial coefficient.

# function to return product of number
# from start to end.
def factorial(start, end):

    res = 1

    for i in range(start, end + 1):
        res *= i

    return res

# Return the sum of square of binomial
# coefficient
def sumofsquare(n):

    return int(factorial(n + 1, 2 * n)
                     /factorial(1, n))

# Driven Program

n = 4
print(sumofsquare(n))


# This code is contributed by
# Smitha Dinesh Semwal

C#

// C# Program to find the sum of square of
// binomial coefficient.
using System;

class GFG {

    // function to return product of number
    // from start to end.
    static int factorial(int start, int end)
    {
        int res = 1;

        for (int i = start; i <= end; i++)
            res *= i;

        return res;
    }

    // Return the sum of square of binomial
    // coefficient
    static int sumofsquare(int n)
    {
        return factorial(n+1, 2*n)/factorial(1, n);
    }

    // Driven Program
    public static void Main()
    {
        int n = 4;

        Console.WriteLine(sumofsquare(n));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// PHP Program to find the sum
// of square of binomial coefficient.

// function to return
// product of number
// from start to end.
function factorial($start, $end)
{
    $res = 1;
    for ($i = $start;
         $i <= $end; $i++)
        $res *= $i;

    return $res;
}

// Return the sum of
// square of binomial
// coefficient
function sumofsquare($n)
{
    return factorial($n + 1,
                     2 * $n) /
           factorial(1, $n);
}

// Driver Code
$n = 4;
echo sumofsquare($n), "\n";

// This code is contributed by ajit
?>

Javascript

<script>

    // Javascript Program to find
    // the sum of square of
    // binomial coefficient.

    // function to return product of number
    // from start to end.
    function factorial(start, end)
    {
        let res = 1;

        for (let i = start; i <= end; i++)
            res *= i;

        return res;
    }

    // Return the sum of square of binomial
    // coefficient
    function sumofsquare(n)
    {
        return parseInt
        (factorial(n+1, 2*n)/factorial(1, n), 10);
    }

    let n = 4;

      document.write(sumofsquare(n));

</script>

Output:

70

Time Complexity: O(n)
Auxiliary Space: O(1)