Sum of the series 0.6, 0.06, 0.006, 0.0006, …to n terms

Given the number of terms i.e. n. Find the sum of the series 0.6, 0.06, 0.006, 0.0006, …to n terms.
Examples:

Input : 2
Output : 0.65934

Input : 3
Output : 0.665334

Let’s denote the sum by S: 
Using the formula 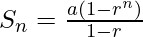, we have [since r<1]



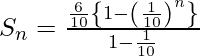
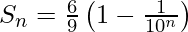
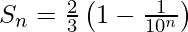
Hence the required sum is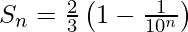 
Below is the implementation: 

C++

// CPP program to find sum of 0.6, 0.06,
// 0.006, 0.0006, ...to n terms
#include <bits/stdc++.h>
using namespace std;

// function which return the
// the sum of series
float sumOfSeries(int n)
{
    return (0.666) * (1 - 1 / pow(10, n));
}

// Driver code
int main()
{
    int n = 2;
    cout << sumOfSeries(n);
}

Java

// java program to find sum of 0.6, 0.06,
// 0.006, 0.0006, ...to n terms
import java.io.*;

class GFG
{
    // function which return the
    // the sum of series
    static double sumOfSeries(int n)
    {
        return (0.666) * (1 - 1 /Math. pow(10, n));
    }


    // Driver code
    public static void main (String[] args)
    {
        int n = 2;
        System.out.println ( sumOfSeries(n));

    }
}

// This code is contributed by vt_m

Python3

# Python3 program to find
# sum of 0.6, 0.06, 0.006,
# 0.0006, ...to n terms
import math

# function which return
# the sum of series
def sumOfSeries(n):
    return ((0.666) *
            (1 - 1 / pow(10, n)));

# Driver code
n = 2;
print(sumOfSeries(n));

# This code is contributed by mits

C#

// C# program to find sum of 0.6, 0.06,
// 0.006, 0.0006, ...to n terms
using System;

class GFG {

    // function which return the
    // the sum of series
    static double sumOfSeries(int n)
    {
        return (0.666) * (1 - 1 /Math. Pow(10, n));
    }

    // Driver code
    public static void Main ()
    {
        int n = 2;

        Console.WriteLine( sumOfSeries(n));

    }
}

// This code is contributed by vt_m

PHP

<?php
// PHP program to find sum of 0.6, 0.06,
// 0.006, 0.0006, ...to n terms

// function which return the
// the sum of series
function sumOfSeries($n)
{
    return (0.666) * (1 - 1 /
                pow(10, $n));
}

// Driver code
$n = 2;
echo(sumOfSeries($n));

// This code is contributed by Ajit.
?>

Javascript

<script>
// javascript program to find sum of 0.6, 0.06,
// 0.006, 0.0006, ...to n terms

// function which return the
// the sum of series
function sumOfSeries( n)
{
    return (0.666) * (1 - 1 / Math.pow(10, n));
}

// Driver Code
let n = 2 ;
   document.write(sumOfSeries(n).toFixed(5)) ;

// This code is contributed by aashish1995

</script>

Output

0.65934

Method2 :

C++

#include <iostream>
#include <cmath>

double sum_of_series(int n) {
    return 0.6 * (1 - pow(1/10.0, n)) / (1 - 1/10.0);
}

int main() {
    int n;
    n=3;
    std::cout << "Sum of the series to " << n << " terms: " << sum_of_series(n) << std::endl;
    return 0;
}

Java

public class Main {
 public static void main(String[] args)
 {
 int n = 3;
 System.out.println("Sum of the series to " + n
 + " terms: " + sumOfSeries(n));
 }
 public static double sumOfSeries(int n)
 {
 return 0.6 * (1 - Math.pow(1 / 10.0, n))
 / (1 - 1 / 10.0);
 }
     }
}

Python3

import math

def sum_of_series(n):
    return 0.6 * (1 - pow(1/10.0, n)) / (1 - 1/10.0)

n = 3
print("Sum of the series to", n, "terms:", sum_of_series(n))

C#

using System;

public class Program {
    public static double SumOfSeries(int n) {
        return 0.6 * (1 - Math.Pow(1.0 / 10, n)) / (1 - 1.0 / 10);
    }

    public static void Main() {
        int n = 3;
        Console.WriteLine("Sum of the series to {0} terms: {1}", n, SumOfSeries(n));
    }
}

Javascript

function sumOfSeries(n) {
  return 0.6 * (1 - Math.pow(1 / 10, n)) / (1 - 1 / 10);
}

let n = 3;
console.log(`Sum of the series to ${n} terms: ${sumOfSeries(n)}`);

Output

Sum of the series to 3 terms: 0.666

Time complexity: O(logn) because using inbuilt pow function
Auxiliary Space: O(1) 

Method3:  

1. This code uses the formula for the sum of the series, which is S = 2*((1 – 1/10^n))/3. 

2. The code initializes an integer variable n to 3, which represents the number of terms in the series to sum. It then computes the sum of the series using the formula and assigns it to a float variable sum. 

3. Finally, the code prints the sum to the console.

Note that we use the math.pow() function from the math module to compute the value of 10^n, since the ** operator in Python does not work with large exponents.

Python3

import math

n = 3
sum = 2*((1 - 1 / math.pow(10, n)))/3
print("Sum of the series to", n, "terms:", sum)

Java

import java.lang.Math;

public class Main {
  public static void main(String[] args) {
    int n = 3;
    double sum = 2*((1 - 1 / Math.pow(10, n)))/3;
    System.out.println("Sum of the series to " + n + " terms: " + sum);
  }
}

C++

#include <iostream>
#include <cmath>

using namespace std;

int main() {
    int n = 3;
    double sum = 2 * ((1 - 1 / pow(10, n))) / 3;
    cout << "Sum of the series to " << n << " terms: " << sum << endl;
    return 0;
}

C#

using System;

class Program {
    static void Main(string[] args) {
        int n = 3;
        double sum = 2 * ((1 - 1 / Math.Pow(10, n))) / 3;
        Console.WriteLine("Sum of the series to {0} terms: {1}", n, sum);
    }
}

Javascript

let n = 3;
let sum = 2 * ((1 - 1 / Math.pow(10, n))) / 3;
console.log(`Sum of the series to ${n} terms: ${sum}`);

Output

Sum of the series to 3 terms: 0.666

Time complexity: O(1) 
Auxiliary Space: O(1)