Sum of width (max and min diff) of all Subsequences
Last Updated :
08 Jun, 2022
Given an array A[] of integers. The task is to return the sum of the width of all subsequences of A. For any sequence S, the width of S is the difference between the maximum and minimum elements of S.
Note: Since the answer can be large, print the answer modulo 10^9 + 7.
Examples:
Input : A[] = {1, 3, 2}
Output : 6
Subsequences are {1}, {2}, {3}, {1, 3}, {1, 2} {3, 2} and {1, 3, 2}. Widths are 0, 0, 0, 2, 1, 1 and 2 respectively. Sum of widths is 6.
Input : A[] = [5, 6, 4, 3, 8]
Output : 87
Input : A[] = [1, 2, 3, 4, 5, 6, 7]
Output : 522
The idea is to first, sort the array as sorting the array won’t affect the final answer. After sorting, this allows us to know that the number of subsequences with minimum A[i] and maximum A[j] will be 2j-i-1.
Hence, our answer boils down to find:
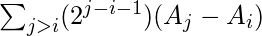 [Tex]= (\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}(2^{j-i-1})(A_{j}))-(\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}(2^{j-i-1})(A_{i}))[/Tex]
[Tex]= (\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}(2^{j-i-1})(A_{j}))-(\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}(2^{j-i-1})(A_{i}))[/Tex]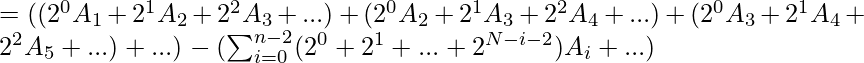 [Tex]= (\sum_{j=1}^{n-1}(2^{j}-1)A_{j})-(\sum_{i=0}^{n-2}(2^{N-i-1}-1)A_{i})[/Tex]
[Tex]= (\sum_{j=1}^{n-1}(2^{j}-1)A_{j})-(\sum_{i=0}^{n-2}(2^{N-i-1}-1)A_{i})[/Tex]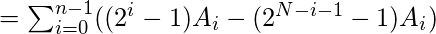 [Tex]= \sum_{i=0}^{n-1}(2^{i}-2^{N-i-1})A_{i}[/Tex]
[Tex]= \sum_{i=0}^{n-1}(2^{i}-2^{N-i-1})A_{i}[/Tex]
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define MOD 1000000007
int SubseqWidths(int A[], int n)
{
sort(A, A + n);
int pow2[n];
pow2[0] = 1;
for (int i = 1; i < n; ++i)
pow2[i] = (pow2[i - 1] * 2) % MOD;
int ans = 0;
for (int i = 0; i < n; ++i)
ans = (ans + (pow2[i] - pow2[n - 1 - i]) * A[i]) % MOD;
return ans;
}
int main()
{
int A[] = { 5, 6, 4, 3, 8 };
int n = sizeof(A) / sizeof(A[0]);
cout << SubseqWidths(A, n);
return 0;
}
|
Java
import java.util.Arrays;
class GFG{
static int MOD=1000000007;
static int SubseqWidths(int[] A, int n)
{
Arrays.sort(A);
int[] pow2=new int[n];
pow2[0] = 1;
for (int i = 1; i < n; ++i)
pow2[i] = (pow2[i - 1] * 2) % MOD;
int ans = 0;
for (int i = 0; i < n; ++i)
ans = (ans + (pow2[i] -
pow2[n - 1 - i]) * A[i]) % MOD;
return ans;
}
public static void main(String[] args)
{
int[] A = new int[]{ 5, 6, 4, 3, 8 };
int n = A.length;
System.out.println(SubseqWidths(A, n));
}
}
|
Python
def SubseqWidths(A):
MOD = 10**9 + 7
N = len(A)
A.sort()
pow2 = [1]
for i in range(1, N):
pow2.append(pow2[-1] * 2 % MOD)
ans = 0
for i, x in enumerate(A):
ans = (ans + (pow2[i] - pow2[N - 1 - i]) * x) % MOD
return ans
A = [5, 6, 4, 3, 8]
print(SubseqWidths(A))
|
C#
using System;
class GFG
{
static int MOD = 1000000007;
static int SubseqWidths(int[] A, int n)
{
Array.Sort(A);
int[] pow2 = new int[n];
pow2[0] = 1;
for (int i = 1; i < n; ++i)
pow2[i] = (pow2[i - 1] * 2) % MOD;
int ans = 0;
for (int i = 0; i < n; ++i)
ans = (ans + (pow2[i] -
pow2[n - 1 - i]) *
A[i]) % MOD;
return ans;
}
static void Main()
{
int[] A = new int[]{ 5, 6, 4, 3, 8 };
int n = A.Length;
Console.WriteLine(SubseqWidths(A, n));
}
}
|
PHP
<?php
$MOD = 1000000007;
function SubseqWidths(&$A, $n)
{
global $MOD;
sort($A);
$pow2 = array_fill(0, $n, NULL);
$pow2[0] = 1;
for ($i = 1; $i < $n; ++$i)
$pow2[$i] = ($pow2[$i - 1] * 2) % $MOD;
$ans = 0;
for ($i = 0; $i < $n; ++$i)
$ans = ($ans + ($pow2[$i] -
$pow2[$n - 1 - $i]) *
$A[$i]) % $MOD;
return $ans;
}
$A = array(5, 6, 4, 3, 8 );
$n = sizeof($A);
echo SubseqWidths($A, $n);
?>
|
Javascript
<script>
var MOD = 1000000007
function SubseqWidths(A, n)
{
A.sort((a,b) => a-b)
var pow2 = Array(n).fill(0);
pow2[0] = 1;
for (var i = 1; i < n; ++i)
pow2[i] = (pow2[i - 1] * 2) % MOD;
var ans = 0;
for (var i = 0; i < n; ++i)
ans = (ans + (pow2[i] - pow2[n - 1 - i]) * A[i]) % MOD;
return ans;
}
var A = [ 5, 6, 4, 3, 8 ];
var n = A.length;
document.write( SubseqWidths(A, n));
</script>
|
Time Complexity: O(N*log(N)), where N is the length of A.
Auxiliary Space: O(N), where N is the length of A.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...