Sum of the numbers upto N that are divisible by 2 or 5
Last Updated :
25 Feb, 2023
Given a number n. The task is to find the sum of numbers up to n, that are divisible by 2 or 5.
Examples:
Input: n = 2
Output: 2
Input: n = 5
Output: 11
A naive approach is to just iterate over the numbers up to n and check if it divisible by 2 or 5. If it is divisible then just add this number to our required sum. And finally, we got our total sum with a complexity of O(n).
Efficient Approach:
1. First find the numbers that are divisible by 2. So, these numbers for an AP, having
first term = 2, difference = 2, Number of terms = n/2
So, sum given by-
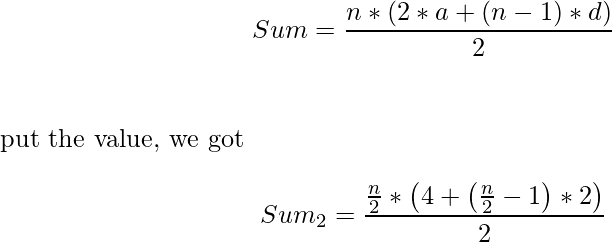
2. Secondly we find the numbers that are divisible by 5. So, these number for an AP, having
first term = 5, difference = 5, Number of terms = n/5
So, sum given by-
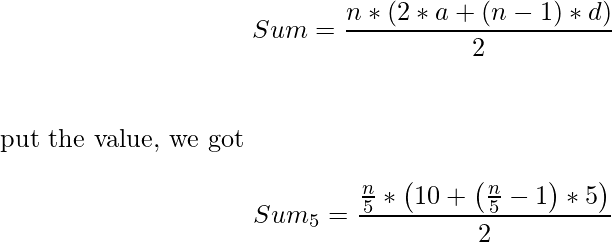
3. First we find the numbers that are divisible by 2 and 5.so, these number for an AP, having
first term =10, difference = 10, Number of terms = n / 10
So, sum given by-
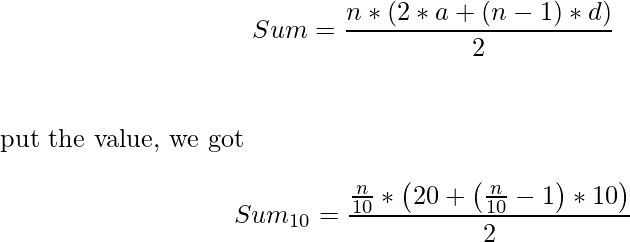
4. As we have to find the sum of numbers divisible by 2 or 5. So, the required sum is given by-
sum = sum_2 + sum_5 – sum_10
Algorithm:
Step 1: Start
Step 2: Create a function with the return type of long and input parameter of int type, find sum will return the sum of numbers divisible by 2 or 5 up to N.
Step 3: Now create three variables of long type say sum2, sum5, sum10
Step 4: Now store the sum of all numbers divided by 2 in sum2 by using the formula : (n / 2) * (4 + (n / 2 – 1) * 2)) / 2
Step 5: Now store the sum of all numbers divided by 5 in sum5 by using the formula : ((n / 5) * (10 + (n / 5 – 1) * 5)) / 2
Step 6: Now store the sum of all numbers divided by 10 in sum10 by using the formula : ((n / 10) * (20 + (n / 10 – 1) * 10)) / 2
Step 7: Now return the sum2 + sum5 – sum10 because it will give sum of the number divisible by 2 or 5.
Step 8: End
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#define ll long long int
using namespace std;
ll findSum(int n)
{
ll sum2, sum5, sum10;
sum2 = ((n / 2) * (4 + (n / 2 - 1) * 2)) / 2;
sum5 = ((n / 5) * (10 + (n / 5 - 1) * 5)) / 2;
sum10 = ((n / 10) * (20 + (n / 10 - 1) * 10)) / 2;
return sum2 + sum5 - sum10;
}
int main()
{
int n = 5;
cout << findSum(n) << endl;
return 0;
}
|
Java
import java.lang.*;
import java.util.*;
class GFG
{
static long findSum(int n)
{
long sum2, sum5, sum10;
sum2 = ((n / 2) * (4 +
(n / 2 - 1) * 2)) / 2;
sum5 = ((n / 5) * (10 +
(n / 5 - 1) * 5)) / 2;
sum10 = ((n / 10) * (20 +
(n / 10 - 1) * 10)) / 2;
return sum2 + sum5 - sum10;
}
public static void main (String[] args)
{
int n = 5;
System.out.println(findSum(n));
}
}
|
Python3
def findSum(n):
sum2 = ((n // 2) * (4 + (n // 2 - 1) * 2)) // 2
sum5 = ((n // 5) * (10 + (n // 5 - 1) * 5)) // 2
sum10 = ((n // 10) * (20 + (n // 10 - 1) * 10)) // 2
return sum2 + sum5 - sum10;
if __name__=='__main__':
n = 5
print (int(findSum(n)))
|
C#
using System;
class GFG
{
static long findSum(int n)
{
long sum2, sum5, sum10;
sum2 = ((n / 2) * (4 +
(n / 2 - 1) * 2)) / 2;
sum5 = ((n / 5) * (10 +
(n / 5 - 1) * 5)) / 2;
sum10 = ((n / 10) * (20 +
(n / 10 - 1) * 10)) / 2;
return sum2 + sum5 - sum10;
}
public static void Main ()
{
int n = 5;
Console.WriteLine(findSum(n));
}
}
|
PHP
<?php
function findSum($n)
{
$sum2 = ((int)($n / 2) * (4 +
((int)($n / 2) - 1) * 2)) / 2;
$sum5 = ((int)($n / 5) * (10 +
($n / 5 - 1) * 5)) / 2;
$sum10 = ((int)($n / 10) * (20 +
($n / 10 - 1) * 10)) / 2;
return $sum2 + $sum5 - $sum10;
}
$n = 5;
echo findSum($n);
?>
|
Javascript
<script>
function findSum(n)
{
var sum2, sum5, sum10;
sum2 = parseInt((parseInt(n / 2) *
(4 + (parseInt(n / 2) - 1) * 2)) / 2);
sum5 = parseInt((parseInt(n / 5) *
(10 + (parseInt(n / 5) - 1) * 5)) / 2);
sum10 = parseInt((parseInt(n / 10) *
(20 + (parseInt(n / 10) - 1) * 10)) / 2);
return sum2 + sum5 - sum10;
}
var n = 5;
document.write( findSum(n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...