Sum of the count of number of adjacent squares in an M X N grid
Last Updated :
10 Mar, 2022
Given an M × N matrix. The task is to count the number of adjacent cells and calculate their sum.
Two cells are said to be connected if they are adjacent to each other horizontally, vertically, or diagonally.
Examples :
Input : m = 2, n = 2
Output : 12
Input : m = 3, n = 2
Output: 22
See the below diagram where numbers written on it denotes number of adjacent squares.
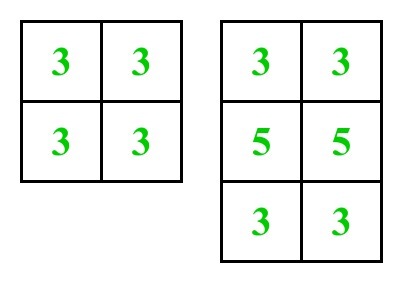
Approach:
In a m X n grid there can be 3 cases:
- Corner cells touch 3 cells, and there are always 4 corner cells.
- Edge cells touch 5 cells, and there are always 2 * (m+n-4) edge cells.
- Interior cells touch 8 cells, and there are always (m-2) * (n-2) interior cells.
Therefore,
Sum = 3*4 + 5*2*(m+n-4) + 8*(m-2)*(n-2)
= 8mn - 6m - 6n +4
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int sum(int m, int n)
{
return 8 * m * n - 6 * m - 6 * n + 4;
}
int main()
{
int m = 3, n = 2;
cout << sum(m, n);
return 0;
}
|
Java
class GFG
{
static int sum(int m, int n)
{
return 8 * m * n - 6 * m - 6 * n + 4;
}
public static void main (String[] args)
{
int m = 3, n = 2;
System.out.println(sum(m, n));
}
}
|
Python3
def summ(m, n):
return 8 * m * n - 6 * m - 6 * n + 4
m = 3
n = 2
print(summ(m, n))
|
C#
using System;
class GFG
{
static int sum(int m, int n)
{
return 8 * m * n - 6 * m - 6 * n + 4;
}
public static void Main (String []args)
{
int m = 3, n = 2;
Console.WriteLine(sum(m, n));
}
}
|
Javascript
<script>
function sum(m, n)
{
return 8 * m * n - 6 * m - 6 * n + 4;
}
var m = 3, n = 2;
document.write(sum(m, n));
</script>
|
Time Complexity: 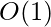
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...