Sum of series 8/10, 8/100, 8/1000, 8/10000. . . till N terms
Last Updated :
23 Dec, 2022
Given a positive integer n, the task is to find the sum of series
8/10 + 8/100 + 8/1000 + 8/10000. . . till Nth term
Examples:
Input: n = 3
Output: 0.888
Input: n = 5
Output: 0.88888
Approach:
The total sum till nth term of the given G.P. series can be generalized as-
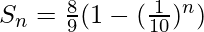
The above formula can be derived following the series of steps-
The given G.P. series
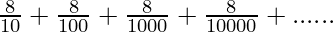
Here,
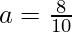
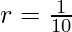
Thus, using the sum of G.P. formula for r<1
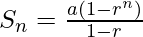
Substituting the values of a and r in the above equation
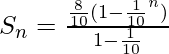
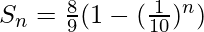
Illustration:
Input: n = 3
Output: 0.888
Explanation:
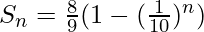
S_{n}=\frac{8}{9}(1-(\frac{1}{10})^{3})
= 0.888 * 0.999
= 0.888
Below is the implementation of the above problem-
C++
#include <bits/stdc++.h>
using namespace std;
double sumOfSeries(double N)
{
return (8 * ((pow(10, N) - 1) / pow(10, N))) / 9;
}
int main()
{
double N = 5;
cout << sumOfSeries(N);
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static double sumOfSeries(double N)
{
return (8
* ((Math.pow(10, N) - 1) / Math.pow(10, N)))
/ 9;
}
public static void main(String args[])
{
double N = 5;
System.out.print(sumOfSeries(N));
}
}
|
Python3
def sumOfSeries(N):
return (8 * (((10 ** N) - 1) / (10 ** N))) / 9;
N = 5;
print(sumOfSeries(N));
|
C#
using System;
class GFG
{
static double sumOfSeries(double N)
{
return (8
* ((Math.Pow(10, N) - 1) / Math.Pow(10, N)))
/ 9;
}
public static void Main()
{
double N = 5;
Console.WriteLine(sumOfSeries(N));
}
}
|
Javascript
<script>
function sumOfSeries(N) {
return (8 * ((Math.pow(10, N) - 1) / Math.pow(10, N))) / 9;
}
let N = 5;
document.write(sumOfSeries(N));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...