Sum of products of all possible K size subsets of the given array
Last Updated :
17 Apr, 2023
Given an array arr[] of N non-negative integers and an integer 1 ? K ? N. The task is to find the sum of the products of all possible subsets of arr[] of size K.
Examples:
Input: arr[] = {1, 2, 3, 4}, K = 2
Output: 35
(1 * 2) + (1 * 3) + (1 * 4) + (2 * 3) + (2 * 4)
+ (3 * 4) = 2 + 3 + 4 + 6 + 8 + 12 = 35
Input: arr[] = {1, 2, 3, 4}, K = 3
Output: 50
Naive approach: Generate all possible subsets of size K and find the resultant product of each subset. Then sum the product obtained for each subset. The time complexity of this solution would be exponential.
C++
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
int K, N;
int getSum(vector<vector<int> > res)
{
long long sum = 0, MOD = 1000000007;
for (vector<int> tempList : res) {
long long tempSum = 1;
for (int val : tempList) {
tempSum = (tempSum * val) % MOD;
}
sum = sum + tempSum;
}
return sum % MOD;
}
void createAllPossibleSubset(int arr[],
vector<vector<int> >& res,
vector<int>& temp, int index)
{
if (temp.size() == K) {
res.push_back(temp);
return;
}
for (int i = index; i < N; i++) {
temp.push_back(arr[i]);
createAllPossibleSubset(arr, res, temp, i + 1);
temp.pop_back();
}
}
int sumOfProduct(int arr[], int n, int k)
{
K = k;
N = n;
vector<vector<int> > res;
vector<int> temp;
createAllPossibleSubset(arr, res, temp, 0);
return getSum(res);
}
int main()
{
int n = 4, k = 2;
int arr[] = { 1, 2, 3, 4 };
cout << sumOfProduct(arr, n, k);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static int K;
public static int sumOfProduct(int arr[], int n, int k)
{
K = k;
ArrayList<ArrayList<Integer> > res
= new ArrayList<>();
createAllPossibleSubset(arr, res, new ArrayList<>(),
0);
return getSum(res);
}
static void createAllPossibleSubset(
int arr[], ArrayList<ArrayList<Integer> > res,
ArrayList<Integer> temp, int index)
{
if (temp.size() == K) {
res.add(new ArrayList<>(temp));
return;
}
for (int i = index; i < arr.length; i++) {
temp.add(arr[i]);
createAllPossibleSubset(arr, res, temp, i + 1);
temp.remove(temp.size() - 1);
}
}
private static int
getSum(ArrayList<ArrayList<Integer> > res)
{
int sum = 0, MOD = 1000000007;
for (ArrayList<Integer> tempList : res) {
long tempSum = 1;
for (int val : tempList) {
tempSum *= val % MOD;
}
sum += tempSum;
}
return sum % MOD;
}
public static void main(String[] args)
{
int n = 4, k = 2;
int arr[] = { 1, 2, 3, 4 };
System.out.println(sumOfProduct(arr, n, k));
}
}
|
Python3
from typing import List, Tuple
def getSum(res: List[List[int]]) -> int:
sum = 0
MOD = 1000000007
for tempList in res:
tempSum = 1
for val in tempList:
tempSum = (tempSum * val) % MOD
sum += tempSum
return sum % MOD
def createAllPossibleSubset(arr: List[int], res: List[List[int]], temp: List[int], index: int, k: int):
if len(temp) == k:
res.append(temp[:])
return
for i in range(index, len(arr)):
temp.append(arr[i])
createAllPossibleSubset(arr, res, temp, i + 1, k)
temp.pop()
def sumOfProduct(arr: List[int], k: int) -> int:
res = []
temp = []
createAllPossibleSubset(arr, res, temp, 0, k)
return getSum(res)
if __name__ == "__main__":
arr = [1, 2, 3, 4]
k = 2
print(sumOfProduct(arr, k))
|
C#
using System;
using System.Collections.Generic;
public class GFG {
static int K;
public static long sumOfProduct(int []arr, int n, int k)
{
K = k;
List<List<int> > res = new List<List<int>>();
createAllPossibleSubset(arr, res, new List<int>(),
0);
return getSum(res);
}
static void createAllPossibleSubset(
int []arr, List<List<int> > res,
List<int> temp, int index)
{
if (temp.Count == K) {
res.Add(new List<int>(temp));
return;
}
for (int i = index; i < arr.Length; i++) {
temp.Add(arr[i]);
createAllPossibleSubset(arr, res, temp, i + 1);
temp.RemoveAt(temp.Count - 1);
}
}
private static long
getSum(List<List<int> > res)
{
long sum = 0, MOD = 1000000007;
foreach (List<int> tempList in res) {
long tempSum = 1;
foreach (int val in tempList) {
tempSum *= val % MOD;
}
sum += tempSum;
}
return sum % MOD;
}
public static void Main(String[] args)
{
int n = 4, k = 2;
int []arr = { 1, 2, 3, 4 };
Console.WriteLine(sumOfProduct(arr, n, k));
}
}
|
Javascript
function getSum(res) {
let sum = 0;
const MOD = 1000000007;
for (let tempList of res) {
let tempSum = 1;
for (let val of tempList) {
tempSum = (tempSum * val) % MOD;
}
sum = sum + tempSum;
}
return sum % MOD;
}
function createAllPossibleSubset(arr, res, temp, index) {
if (temp.length === K) {
res.push(temp);
return;
}
for (let i = index; i < N; i++) {
temp.push(arr[i]);
createAllPossibleSubset(arr, res, temp, i + 1);
temp.pop();
}
}
function sumOfProduct(arr, n, k) {
K = k;
N = n;
let res = [];
let temp = [];
createAllPossibleSubset(arr, res, temp, 0);
return getSum(res);
}
const n = 4;
const k = 2;
const arr = [1, 2, 3, 4];
console.log(sumOfProduct(arr, n, k));
|
Time Complexity: 2n
Auxiliary Space: 2n ( n is the array size )
Efficient approach: Take the example of an array a[] = {1, 2, 3} and K = 3. Then,
k = 1, answer = 1 + 2 + 3 = 6
k = 2, answer = 1 * (2 + 3) + 2 * 3 + 0 = 11
k = 3, answer = 1 * (2 * 3 + 0) + 0 + 0 = 6
In the example, if the contribution of 1 is needed to be obtained in the answer for K = 2 then the sum of all elements after the index of element 1 is required in the previously computed values for K = 1. It can be seen that the sum of elements 2 and 3 is required. Thus, for any K, the answer obtained for K – 1 is required.
So, bottom-up dynamic programming approach can be used to solve this problem. Create a table dp[][] and fill it in bottom up manner where dp[i][j] will store the contribution of an element arr[j – 1] to the answer for K = i. Hence, the recurrence relation will be,
dp[i][j] = arr[j-1] * 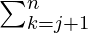
dp[i-1][k]
answer[k] = 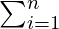
dp[k][i]
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int sumOfProduct(int arr[], int n, int k)
{
int dp[k + 1][n + 1] = { 0 };
int cur_sum = 0;
for (int i = 1; i <= n; i++) {
dp[1][i] = arr[i - 1];
cur_sum += arr[i - 1];
}
for (int i = 2; i <= k; i++) {
int temp_sum = 0;
for (int j = 1; j <= n; j++) {
cur_sum -= dp[i - 1][j];
dp[i][j] = arr[j - 1] * cur_sum;
temp_sum += dp[i][j];
}
cur_sum = temp_sum;
}
return cur_sum;
}
int main()
{
int arr[] = { 1, 2, 3, 4 };
int n = sizeof(arr) / sizeof(int);
int k = 2;
cout << sumOfProduct(arr, n, k);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int sumOfProduct(int arr[], int n,
int k)
{
int dp[][] = new int[n + 1][n + 1];
for(int i = 0; i <= n; i++)
for(int j = 0; j <= n; j++)
dp[i][j] = 0;
int cur_sum = 0;
for(int i = 1; i <= n; i++)
{
dp[1][i] = arr[i - 1];
cur_sum += arr[i - 1];
}
for(int i = 2; i <= k; i++)
{
int temp_sum = 0;
for(int j = 1; j <= n; j++)
{
cur_sum -= dp[i - 1][j];
dp[i][j] = arr[j - 1] * cur_sum;
temp_sum += dp[i][j];
}
cur_sum = temp_sum;
}
return cur_sum;
}
public static void main(String[] args)
{
int arr[] = { 1, 2, 3, 4 };
int n = arr.length;
int k = 2;
System.out.print(sumOfProduct(arr, n, k));
}
}
|
Python3
def sumOfProduct(arr, n, k):
dp = [ [ 0 for x in range(n + 1)] for y in range(n + 1)]
cur_sum = 0
for i in range(1, n + 1):
dp[1][i] = arr[i - 1]
cur_sum += arr[i - 1]
for i in range(2 , k + 1):
temp_sum = 0
for j in range( 1, n + 1):
cur_sum -= dp[i - 1][j]
dp[i][j] = arr[j - 1] * cur_sum
temp_sum += dp[i][j]
cur_sum = temp_sum
return cur_sum
if __name__ == "__main__":
arr = [ 1, 2, 3, 4 ]
n = len(arr)
k = 2
print(sumOfProduct(arr, n, k))
|
C#
using System.Collections.Generic;
using System;
class GFG{
static int sumOfProduct(int []arr, int n, int k)
{
int [,]dp = new int[n + 1, n + 1];
for(int i = 0; i <= n; i++)
for(int j = 0; j <= n; j++)
dp[i, j] = 0;
int cur_sum = 0;
for(int i = 1; i <= n; i++)
{
dp[1, i] = arr[i - 1];
cur_sum += arr[i - 1];
}
for(int i = 2; i <= k; i++)
{
int temp_sum = 0;
for(int j = 1; j <= n; j++)
{
cur_sum -= dp[i - 1, j];
dp[i, j] = arr[j - 1] * cur_sum;
temp_sum += dp[i, j];
}
cur_sum = temp_sum;
}
return cur_sum;
}
public static void Main()
{
int []arr = { 1, 2, 3, 4 };
int n = arr.Length;
int k = 2;
Console.WriteLine(sumOfProduct(arr, n, k));
}
}
|
Javascript
<script>
function sumOfProduct(arr, n, k)
{
let dp = new Array(n + 1);
for(let i = 0; i < dp.length; i++)
{
dp[i] = new Array(n + 1);
for(let j = 0; j < dp[i].length; j++)
{
dp[i][j] = 0;
}
}
let cur_sum = 0;
for(let i = 1; i <= n; i++)
{
dp[1][i] = arr[i - 1];
cur_sum += arr[i - 1];
}
for(let i = 2; i <= k; i++)
{
let temp_sum = 0;
for(let j = 1; j <= n; j++)
{
cur_sum -= dp[i - 1][j];
dp[i][j] = arr[j - 1] * cur_sum;
temp_sum += dp[i][j];
}
cur_sum = temp_sum;
}
return cur_sum;
}
let arr = [ 1, 2, 3, 4 ];
let n = arr.length;
let k = 2;
document.write(sumOfProduct(arr, n, k));
</script>
|
Time Complexity: O(n2)
Auxiliary Space: O(k*n)
Efficient approach : Space Optimization
to optimize the space complexity of previous approach we using a 1D array instead of a 2D array to store the values of the DP table. Since we only need the values of the previous row to compute the values of the current row, we can use a single array to store these values and update it as we iterate over the rows
Implementation Steps:
- Initialize an array dp of size n+1 to store the computed values.
- Initialize cur_sum variable to 0.
- Fill the first row of the dp table with the values from the input array arr.
- Compute the sum of all elements in arr and store it in cur_sum.
- For each value of i from 2 to k, perform the following:
a. Set temp_sum to 0.
b. For each value of j from 1 to n, perform the following:
i. Subtract the previously computed value from dp[j] to get the sum of elements from j + 1 to n in the (i – 1)th row.
ii. Multiply the value of arr[j-1] with the current sum computed in step (i) and store it in dp[j].
iii. Add the value of dp[j] to temp_sum. - c. Update the value of cur_sum with the value of temp_sum.
- Return the value of cur_sum.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int sumOfProduct(int arr[], int n, int k)
{
int dp[n + 1] = { 0 };
int cur_sum = 0;
for (int i = 1; i <= n; i++) {
dp[i] = arr[i - 1];
cur_sum += arr[i - 1];
}
for (int i = 2; i <= k; i++) {
int temp_sum = 0;
for (int j = 1; j <= n; j++) {
cur_sum -= dp[j];
dp[j] = arr[j - 1] * cur_sum;
temp_sum += dp[j];
}
cur_sum = temp_sum;
}
return cur_sum;
}
int main()
{
int arr[] = { 1, 2, 3, 4 };
int n = sizeof(arr) / sizeof(int);
int k = 2;
cout << sumOfProduct(arr, n, k);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int sumOfProduct(int[] arr, int n, int k)
{
int[] dp = new int[n + 1];
int cur_sum = 0;
for (int i = 1; i <= n; i++) {
dp[i] = arr[i - 1];
cur_sum += arr[i - 1];
}
for (int i = 2; i <= k; i++) {
int temp_sum = 0;
for (int j = 1; j <= n; j++) {
cur_sum -= dp[j];
dp[j] = arr[j - 1] * cur_sum;
temp_sum += dp[j];
}
cur_sum = temp_sum;
}
return cur_sum;
}
public static void main(String[] args)
{
int[] arr = { 1, 2, 3, 4 };
int n = arr.length;
int k = 2;
System.out.println(sumOfProduct(arr, n, k));
}
}
|
Python3
def sumOfProduct(arr, n, k):
dp = [0] * (n + 1)
cur_sum = 0
for i in range(1, n + 1):
dp[i] = arr[i - 1]
cur_sum += arr[i - 1]
for i in range(2, k + 1):
temp_sum = 0
for j in range(1, n + 1):
cur_sum -= dp[j]
dp[j] = arr[j - 1] * cur_sum
temp_sum += dp[j]
cur_sum = temp_sum
return cur_sum
arr = [1, 2, 3, 4]
n = len(arr)
k = 2
print(sumOfProduct(arr, n, k))
|
C#
using System;
class GFG {
static int SumOfProduct(int[] arr, int n, int k)
{
int[] dp = new int[n + 1];
int cur_sum = 0;
for (int i = 1; i <= n; i++) {
dp[i] = arr[i - 1];
cur_sum += arr[i - 1];
}
for (int i = 2; i <= k; i++) {
int temp_sum = 0;
for (int j = 1; j <= n; j++) {
cur_sum -= dp[j];
dp[j] = arr[j - 1] * cur_sum;
temp_sum += dp[j];
}
cur_sum = temp_sum;
}
return cur_sum;
}
static void Main(string[] args)
{
int[] arr = { 1, 2, 3, 4 };
int n = arr.Length;
int k = 2;
Console.WriteLine(SumOfProduct(arr, n, k));
}
}
|
Javascript
function sumOfProduct(arr, n, k) {
let dp = new Array(n + 1).fill(0);
let cur_sum = 0;
for (let i = 1; i <= n; i++) {
dp[i] = arr[i - 1];
cur_sum += arr[i - 1];
}
for (let i = 2; i <= k; i++) {
let temp_sum = 0;
for (let j = 1; j <= n; j++) {
cur_sum -= dp[j];
dp[j] = arr[j - 1] * cur_sum;
temp_sum += dp[j];
}
cur_sum = temp_sum;
}
return cur_sum;
}
let arr = [1, 2, 3, 4];
let n = arr.length;
let k = 2;
console.log(sumOfProduct(arr, n, k));
|
Output
35
Time Complexity: O(N*K)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...