Sum of N-terms of geometric progression for larger values of N | Set 2 (Using recursion)
Last Updated :
02 Mar, 2022
A Geometric series is a series with a constant ratio between successive terms. The first term of the series is denoted by a and the common ratio is denoted by r. The series looks like this:- 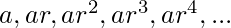
The task is to find the sum of such a series, mod M.
Examples:
Input: a = 1, r = 2, N = 10000, M = 10000
Output: 8751
Input: a = 1, r = 4, N = 10000, M = 100000
Output: 12501
Approach:
- To find the sum of series
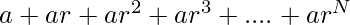 we can easily take a as common and find the sum of
we can easily take a as common and find the sum of 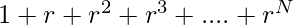 and multiply it with a.
and multiply it with a. - Steps to find the sum of the above series.
- Here, it can be resolved that:
![Rendered by QuickLaTeX.com [1 + r + r^2 + r^3 + . . . + r^(2*n+1)] = (1+r)*(1 + (r^2) + (r^2)^2 + (r^2)^3 + . . . + (r^2)^n)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c5c0047135be8e0d7abe9ebe94b9a606_l3.png)
If we denote,
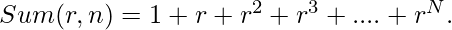 then,
then,
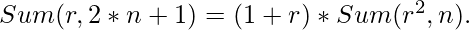 and,
and,
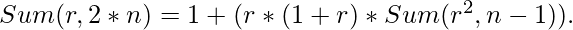
This will work as our recursive case.
Sum(r, 0) = 1.
Sum(r, 1) = 1 + r.
Below is the implementation of the above approach.
C++
#include <iostream>
using namespace std;
int SumGPUtil(long long int r,
long long int n,
long long int m)
{
if (n == 0)
return 1;
if (n == 1)
return (1 + r) % m;
long long int ans;
if (n % 2 == 1)
{
ans = (1 + r) *
SumGPUtil((r * r) % m,
(n - 1) / 2, m);
}
else
{
ans = 1 + (r * (1 + r) *
SumGPUtil((r * r) % m,
(n / 2) - 1, m));
}
return (ans % m);
}
void SumGP(long long int a,
long long int r,
long long int N,
long long int M)
{
long long int answer;
answer = a * SumGPUtil(r, N, M);
answer = answer % M;
cout << answer << endl;
}
int main()
{
long long int a = 1;
long long int r = 4;
long long int N = 10000;
long long int M = 100000;
SumGP(a, r, N, M);
return 0;
}
|
Java
import java.io.*;
class GFG{
static long SumGPUtil(long r, long n,
long m)
{
if (n == 0)
return 1;
if (n == 1)
return (1 + r) % m;
long ans;
if (n % 2 == 1)
{
ans = (1 + r) *
SumGPUtil((r * r) % m,
(n - 1) / 2, m);
}
else
{
ans = 1 + (r * (1 + r) *
SumGPUtil((r * r) % m,
(n / 2) - 1, m));
}
return (ans % m);
}
static void SumGP(long a, long r,
long N, long M)
{
long answer;
answer = a * SumGPUtil(r, N, M);
answer = answer % M;
System.out.println(answer);
}
public static void main (String[] args)
{
long a = 1;
long r = 4;
long N = 10000;
long M = 100000;
SumGP(a, r, N, M);
}
}
|
Python3
def SumGPUtil (r, n, m):
if n == 0: return 1
if n == 1: return (1 + r) % m
if n % 2 == 1:
ans = (1 + r) * SumGPUtil(r * r % m,
(n - 1)//2,
m)
else:
ans = 1 + r * (1 + r) * SumGPUtil(r * r % m,
n//2 - 1,
m)
return ans % m
def SumGP (a, r, N, M):
answer = a * SumGPUtil(r, N, M)
answer = answer % M
print(answer)
if __name__== '__main__':
a = 1
r = 4
N = 10000
M = 100000
SumGP(a, r, N, M)
|
C#
using System;
class GFG{
static long SumGPUtil(long r, long n,
long m)
{
if (n == 0)
return 1;
if (n == 1)
return (1 + r) % m;
long ans;
if (n % 2 == 1)
{
ans = (1 + r) *
SumGPUtil((r * r) % m,
(n - 1) / 2, m);
}
else
{
ans = 1 + (r * (1 + r) *
SumGPUtil((r * r) % m,
(n / 2) - 1, m));
}
return (ans % m);
}
static void SumGP(long a, long r,
long N, long M)
{
long answer;
answer = a * SumGPUtil(r, N, M);
answer = answer % M;
Console.WriteLine(answer);
}
public static void Main()
{
long a = 1;
long r = 4;
long N = 10000;
long M = 100000;
SumGP(a, r, N, M);
}
}
|
Javascript
<script>
function SumGPUtil(r, n, m)
{
if (n == 0)
return 1;
if (n == 1)
return (1 + r) % m;
let ans;
if (n % 2 == 1)
{
ans = (1 + r) *
SumGPUtil((r * r) % m,
(n - 1) / 2, m);
}
else
{
ans = 1 + (r * (1 + r) *
SumGPUtil((r * r) % m,
(n / 2) - 1, m));
}
return (ans % m);
}
function SumGP(a, r, N, M)
{
let answer;
answer = a * SumGPUtil(r, N, M);
answer = answer % M;
document.write(answer);
}
let a = 1;
let r = 4;
let N = 10000;
let M = 100000;
SumGP(a, r, N, M);
</script>
|
Time complexity: O(log N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...