Sum of first n terms of a given series 3, 6, 11, …..
Last Updated :
11 Jul, 2022
Given a series and a number n, the task is to find the sum of its first n terms. Below is the series:
3, 6, 11, 20, ….
Examples:
Input: N = 2
Output: 9
The sum of first 2 terms of Series is
3 + 6 = 9
Input: N = 3
Output: 20
The sum of first 3 terms of Series is
3 + 6 + 11 = 20
Approach: This problem can easily solved by observing that the nth term of the series :
Sn = 3 + 6 + 11 + 20 … + upto nth term
Sn = (1 + 2^1) + (2 + 2^2) + (3 + 2^3)+ (4 + 2^4) …… + upto nth term
Sn = (1 + 2 + 3 + 4 …. + upto nth term) + ( 2^1 + 2^2 + 2^3 …… + unto nth term )
We observe that Sn is a summation of two series: AP and GP
As we know the sum of first n terms of AP is given by
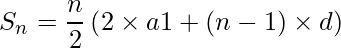
And also the Sum of first n terms of G.P is given by
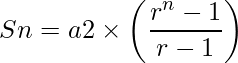
Hence the total sum is given by sum of both AP and GP.
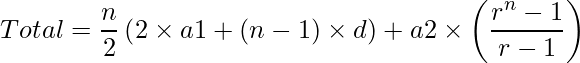
Below is the implementation of above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int calculateSum(int n)
{
int a1 = 1, a2 = 2;
int r = 2;
int d = 1;
return (n) * (2 * a1 + (n - 1) * d) / 2 + a2
* (pow(r, n) - 1) / (r - 1);
}
int main()
{
int n = 5;
cout << "Sum = " << calculateSum(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int calculateSum(int n)
{
int a1 = 1, a2 = 2;
int r = 2;
int d = 1;
return (n) * (2 * a1 + (n - 1) * d) / 2 + a2
* (int)(Math.pow(r, n) - 1) / (r - 1);
}
public static void main (String[] args) {
int n = 5;
System.out.print( "Sum = " + calculateSum(n));
}
}
|
Python3
def calculateSum(n):
a1 = 1;
a2 = 2;
r = 2;
d = 1;
return ((n) * (2 * a1 + (n - 1) * d) /
2 + a2 * (pow(r, n) - 1) /
(r - 1));
n = 5;
print ("Sum =", int(calculateSum(n)))
|
C#
using System;
class GFG
{
static int calculateSum(int n)
{
int a1 = 1, a2 = 2;
int r = 2;
int d = 1;
return (n) * (2 * a1 + (n - 1) * d) / 2 + a2 *
(int)(Math.Pow(r, n) - 1) / (r - 1);
}
public static void Main ()
{
int n = 5;
Console.WriteLine("Sum = " + calculateSum(n));
}
}
|
PHP
<?php
function calculateSum($n)
{
$a1 = 1;
$a2 = 2;
$r = 2;
$d = 1;
return ($n) * (2 * $a1 + ($n - 1) * $d) / 2 +
$a2 * (pow($r, $n) - 1) / ($r - 1);
}
$n = 5;
echo "Sum = ", calculateSum($n);
?>
|
Javascript
<script>
function calculateSum(n)
{
let a1 = 1, a2 = 2;
let r = 2;
let d = 1;
return (n) * (2 * a1 + (n - 1) * d) / 2 + a2
* (Math.pow(r, n) - 1) / (r - 1);
}
let n = 5;
document.write("Sum = " + calculateSum(n));
</script>
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...