Sum of first N natural numbers which are not powers of K

Given two integers 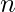and 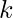, the task is to find the sum of all the numbers within the range [1, n] excluding the numbers which are positive powers of k i.e. the numbers k, k², k³ and so on.
Examples:

Input: n = 10, k = 3 
Output: 43 
1 + 2 + 4 + 5 + 6 + 7 + 8 + 10 = 43 
3 and 9 are excluded as they are powers of 3
Input: n = 11, k = 2 
Output: 52 

Approach:

Approach to solve this problem is to iterate over all the numbers in the range [1, n] and exclude the numbers which are positive powers of k. We can use the logarithm function to check if a number is a positive power of k or not. If a number x is a positive power of k, then it can be represented as k^y for some integer y. Therefore, logk(x) will be an integer if x is a positive power of k.

The steps of the approach are as follows:

1. Initialize a variable sum to one.
2. Iterate over all the numbers from 1 to n.
3. Check if the current number is a positive power of k using the logarithm function. If it is not a positive power of k, then add it to the sum.
4. Return the sum.

Below is the implemenation of the above approach:

C++

#include <iostream>

// Function to check if the given number is a power of k or not
bool isPowerOfK(int num, int k) {
    while (num > 1) {
        if (num % k != 0)
            return false;
        num /= k;
    }
    return num == 1;
}

// Function to return the sum of first n natural numbers which are not positive powers of k
int findSum(int n, int k) {
    int sum = 1;
    for (int i = 1; i <= n; i++) {
        if (!isPowerOfK(i, k))
            sum += i;
    }
    return sum;
}

// Driver code
int main() {
    int n = 11;
    int k = 2;
    std::cout << findSum(n, k) << std::endl;
    return 0;
}

Java

public class Main {
    // Function to check if the given number is a power of k or not
    static boolean isPowerOfK(int num, int k) {
        while (num > 1) {
            if (num % k != 0)
                return false;
            num /= k;
        }
        return (num == 1);
    }

    // Function to return the sum of first n natural numbers which are not positive powers of k
    static int findSum(int n, int k) {
        int sum = 1;
        for (int i = 1; i <= n; i++) {
            if (!isPowerOfK(i, k))
                sum += i;
        }
        return sum;
    }

    // Driver code
    public static void main(String[] args) {
        int n = 11, k = 2;
        System.out.println(findSum(n, k));
    }
}

Python

# Function to check if the given number is a power of k or not
def is_power_of_k(num, k):
    while num > 1:
        if num % k != 0:
            return False
        num //= k
    return num == 1

# Function to return the sum of first n natural numbers which are not positive powers of k
def find_sum(n, k):
    sum = 1
    for i in range(1, n + 1):
        if not is_power_of_k(i, k):
            sum += i
    return sum

# Driver code
def main():
    n = 11
    k = 2
    print(find_sum(n, k))

if __name__ == "__main__":
    main()

C#

using System;

class MainClass {
    // Function to check if the given number is a power of k or not
    static bool IsPowerOfK(int num, int k) {
        while (num > 1) {
            if (num % k != 0)
                return false;
            num /= k;
        }
        return num == 1;
    }

    // Function to return the sum of first n natural numbers which are not positive powers of k
    static int FindSum(int n, int k) {
        int sum = 1;
        for (int i = 1; i <= n; i++) {
            if (!IsPowerOfK(i, k))
                sum += i;
        }
        return sum;
    }

    // Driver code
    public static void Main(string[] args) {
        int n = 11;
        int k = 2;
        Console.WriteLine(FindSum(n, k));
    }
}

Javascript

// Function to check if the given number is a power of k or not
function isPowerOfK(num, k) {
  while (num > 1) {
    if (num % k !== 0)
      return false;
    num /= k;
  }
  return num === 1;
}

// Function to return the sum of the first n natural numbers which are not positive powers of k
function findSum(n, k) {
  let sum = 1;
  for (let i = 1; i <= n; i++) {
    if (!isPowerOfK(i, k))
      sum += i;
  }
  return sum;
}

// Main function
function main() {
  const n = 11;
  const k = 2;
  console.log(findSum(n, k));
}

// Call the main function
main();

Output: 52

Time Complexity: O(n log n), where log n is the time taken to compute the logarithm of a number.

Space Complexity:  O(1), as we are only using constant amount of extra space.

Approach:

• Store the sum of first 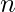natural numbers in a variable 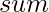i.e. sum = (n * (n + 1)) / 2.
• Now for every positive power of 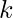which is less than 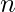, subtract it from the .
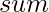• Print the value of the variable 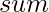in the end.

Below is the implementation of the above approach: 

C++

// C++ program to find the sum of
// first n natural numbers which are
// not positive powers of k
#include <bits/stdc++.h>
using namespace std;

// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
int find_sum(int n, int k)
{
    // sum of first n natural numbers
    int total_sum = (n * (n + 1)) / 2;

    int power = k;
    while (power <= n) {

        // subtract all positive powers
        // of k which are less than n
        total_sum -= power;

        // next power of k
        power *= k;
    }

    return total_sum;
}

// Driver code
int main()
{
    int n = 11, k = 2;

    cout << find_sum(n, k);

    return 0;
}

Java

// Java program to find the sum of
// first n natural numbers which are
// not positive powers of k
import java.io.*;

class GFG {



// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
static int find_sum(int n, int k)
{
    // sum of first n natural numbers
    int total_sum = (n * (n + 1)) / 2;

    int power = k;
    while (power <= n) {

        // subtract all positive powers
        // of k which are less than n
        total_sum -= power;

        // next power of k
        power *= k;
    }

    return total_sum;
}

// Driver code

    public static void main (String[] args) {
        int n = 11, k = 2;

    System.out.println(find_sum(n, k));
    }
}
// This code is contributed by inder_verma..

Python3

# Python 3 program to find the sum of
# first n natural numbers which are
# not positive powers of k

# Function to return the sum of
# first n natural numbers which are
# not positive powers of k
def find_sum(n, k):

    # sum of first n natural numbers
    total_sum = (n * (n + 1)) // 2
    power = k
    while power <= n:

        # subtract all positive powers
        # of k which are less than n
        total_sum -= power

        # next power of k
        power *= k
    return total_sum

# Driver code
n = 11; k = 2
print(find_sum(n, k))

# This code is contributed
# by Shrikant13

C#

// C# program to find the sum of
// first n natural numbers which are
// not positive powers of k
using System;

class GFG {



// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
static int find_sum(int n, int k)
{
    // sum of first n natural numbers
    int total_sum = (n * (n + 1)) / 2;

    int power = k;
    while (power <= n) {

        // subtract all positive powers
        // of k which are less than n
        total_sum -= power;

        // next power of k
        power *= k;
    }

    return total_sum;
}

// Driver code

    public static void Main () {
        int n = 11, k = 2;

    Console.WriteLine(find_sum(n, k));
    }
}
// This code is contributed by inder_verma..

Javascript

<script>

// Javascript program to find the sum of
// first n natural numbers which are
// not positive powers of k

// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
function find_sum(n, k)
{
    // sum of first n natural numbers
    let total_sum = (n * (n + 1)) / 2;

    let power = k;
    while (power <= n) {

        // subtract all positive powers
        // of k which are less than n
        total_sum -= power;

        // next power of k
        power *= k;
    }

    return total_sum;
}

// Driver code
    let n = 11, k = 2;

    document.write(find_sum(n, k));

// This code is contributed by Mayank Tyagi

</script>

PHP

<?php
// PHP program to find the sum of
// first n natural numbers which are
// not positive powers of k

// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
function find_sum($n, $k)
{
    // sum of first n natural numbers
    $total_sum = ($n * ($n + 1)) / 2;

    $power = $k;
    while ($power <= $n)
    {

        // subtract all positive powers
        // of k which are less than n
        $total_sum -= $power;

        // next power of k
        $power *= $k;
    }

    return $total_sum;
}

// Driver code
$n = 11; $k = 2;

echo find_sum($n, $k);

// This code is contributed by inder_verma..
?>

Output

52

Time Complexity: O(log_kn), where n and k represents the value of the given integers.
Auxiliary Space: O(1), no extra space is required, so it is a constant.