Sum of first N natural numbers which are not powers of K
Last Updated :
26 Sep, 2023
Given two integers 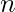 and
and 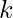 , the task is to find the sum of all the numbers within the range [1, n] excluding the numbers which are positive powers of k i.e. the numbers k, k2, k3 and so on.
, the task is to find the sum of all the numbers within the range [1, n] excluding the numbers which are positive powers of k i.e. the numbers k, k2, k3 and so on.
Examples:
Input: n = 10, k = 3
Output: 43
1 + 2 + 4 + 5 + 6 + 7 + 8 + 10 = 43
3 and 9 are excluded as they are powers of 3
Input: n = 11, k = 2
Output: 52
Approach:
Approach to solve this problem is to iterate over all the numbers in the range [1, n] and exclude the numbers which are positive powers of k. We can use the logarithm function to check if a number is a positive power of k or not. If a number x is a positive power of k, then it can be represented as k^y for some integer y. Therefore, logk(x) will be an integer if x is a positive power of k.
The steps of the approach are as follows:
- Initialize a variable sum to one.
- Iterate over all the numbers from 1 to n.
- Check if the current number is a positive power of k using the logarithm function. If it is not a positive power of k, then add it to the sum.
- Return the sum.
Below is the implemenation of the above approach:
C++
#include <iostream>
bool isPowerOfK(int num, int k) {
while (num > 1) {
if (num % k != 0)
return false;
num /= k;
}
return num == 1;
}
int findSum(int n, int k) {
int sum = 1;
for (int i = 1; i <= n; i++) {
if (!isPowerOfK(i, k))
sum += i;
}
return sum;
}
int main() {
int n = 11;
int k = 2;
std::cout << findSum(n, k) << std::endl;
return 0;
}
|
Java
public class Main {
static boolean isPowerOfK(int num, int k) {
while (num > 1) {
if (num % k != 0)
return false;
num /= k;
}
return (num == 1);
}
static int findSum(int n, int k) {
int sum = 1;
for (int i = 1; i <= n; i++) {
if (!isPowerOfK(i, k))
sum += i;
}
return sum;
}
public static void main(String[] args) {
int n = 11, k = 2;
System.out.println(findSum(n, k));
}
}
|
Python
def is_power_of_k(num, k):
while num > 1:
if num % k != 0:
return False
num //= k
return num == 1
def find_sum(n, k):
sum = 1
for i in range(1, n + 1):
if not is_power_of_k(i, k):
sum += i
return sum
def main():
n = 11
k = 2
print(find_sum(n, k))
if __name__ == "__main__":
main()
|
C#
using System;
class MainClass {
static bool IsPowerOfK(int num, int k) {
while (num > 1) {
if (num % k != 0)
return false;
num /= k;
}
return num == 1;
}
static int FindSum(int n, int k) {
int sum = 1;
for (int i = 1; i <= n; i++) {
if (!IsPowerOfK(i, k))
sum += i;
}
return sum;
}
public static void Main(string[] args) {
int n = 11;
int k = 2;
Console.WriteLine(FindSum(n, k));
}
}
|
Javascript
function isPowerOfK(num, k) {
while (num > 1) {
if (num % k !== 0)
return false;
num /= k;
}
return num === 1;
}
function findSum(n, k) {
let sum = 1;
for (let i = 1; i <= n; i++) {
if (!isPowerOfK(i, k))
sum += i;
}
return sum;
}
function main() {
const n = 11;
const k = 2;
console.log(findSum(n, k));
}
main();
|
Output: 52
Time Complexity: O(n log n), where log n is the time taken to compute the logarithm of a number.
Space Complexity: O(1), as we are only using constant amount of extra space.
Approach:
- Store the sum of first
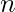 natural numbers in a variable
natural numbers in a variable 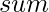 i.e. sum = (n * (n + 1)) / 2.
i.e. sum = (n * (n + 1)) / 2. - Now for every positive power of
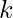 which is less than
which is less than 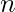 , subtract it from the
, subtract it from the 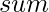 .
. - Print the value of the variable
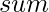 in the end.
in the end.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int find_sum(int n, int k)
{
int total_sum = (n * (n + 1)) / 2;
int power = k;
while (power <= n) {
total_sum -= power;
power *= k;
}
return total_sum;
}
int main()
{
int n = 11, k = 2;
cout << find_sum(n, k);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int find_sum(int n, int k)
{
int total_sum = (n * (n + 1)) / 2;
int power = k;
while (power <= n) {
total_sum -= power;
power *= k;
}
return total_sum;
}
public static void main (String[] args) {
int n = 11, k = 2;
System.out.println(find_sum(n, k));
}
}
|
Python3
def find_sum(n, k):
total_sum = (n * (n + 1)) // 2
power = k
while power <= n:
total_sum -= power
power *= k
return total_sum
n = 11; k = 2
print(find_sum(n, k))
|
C#
using System;
class GFG {
static int find_sum(int n, int k)
{
int total_sum = (n * (n + 1)) / 2;
int power = k;
while (power <= n) {
total_sum -= power;
power *= k;
}
return total_sum;
}
public static void Main () {
int n = 11, k = 2;
Console.WriteLine(find_sum(n, k));
}
}
|
Javascript
<script>
function find_sum(n, k)
{
let total_sum = (n * (n + 1)) / 2;
let power = k;
while (power <= n) {
total_sum -= power;
power *= k;
}
return total_sum;
}
let n = 11, k = 2;
document.write(find_sum(n, k));
</script>
|
PHP
<?php
function find_sum($n, $k)
{
$total_sum = ($n * ($n + 1)) / 2;
$power = $k;
while ($power <= $n)
{
$total_sum -= $power;
$power *= $k;
}
return $total_sum;
}
$n = 11; $k = 2;
echo find_sum($n, $k);
?>
|
Time Complexity: O(logkn), where n and k represents the value of the given integers.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...