Sum of Fibonacci Numbers | Set 2

Given a positive number N, the task is to find the sum of the first (N + 1) Fibonacci Numbers.

Examples:

Input: N = 3
Output: 4
Explanation:
The first 4 terms of the Fibonacci Series is {0, 1, 1, 2}. Therefore, the required sum = 0 + 1 + 1 + 2 = 4.

Input: N = 4
Output: 7

Naive Approach: For the simplest approach to solve the problem, refer to the previous post of this article. 
Time Complexity: O(N)
Auxiliary Space: O(1)

Efficient Approach: The above approach can be optimized by the following observations and calculations:

Let S(N) represent the sum of the first N terms of Fibonacci Series. Now, in order to simply find S(N), calculate the (N + 2)^th Fibonacci number and subtract 1 from the result. The N^th term of this series can be calculated by the formula:

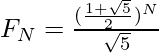
Now the value of S(N) can be calculated by (F_{N + 2} – 1).

Therefore, the idea is to calculate the value of S_N using the above formula:

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to find the sum of
// first N + 1 fibonacci numbers
void sumFib(int N)
{

    // Apply the formula
    long num = (long)round(pow((sqrt(5) + 1)
                               / 2.0, N + 2)
                           / sqrt(5));

    // Print the result
    cout << (num - 1);
}

// Driver Code
int main()
{
    int N = 3;
    sumFib(N);
    return 0;
}

// This code is contributed by Dharanendra L V.

Java

// Java program for the above approach
import java.io.*;

class GFG {

    // Function to find the sum of
    // first N + 1 fibonacci numbers
    public static void sumFib(int N)
    {
        // Apply the formula
        long num = (long)Math.round(
            Math.pow((Math.sqrt(5) + 1)
                         / 2.0,
                     N + 2)
            / Math.sqrt(5));

        // Print the result
        System.out.println(num - 1);
    }

    // Driver Code
    public static void main(String[] args)
    {
        int N = 3;
        sumFib(N);
    }
}

Python3

# Python program for the above approach
import math

# Function to find the sum of
# first N + 1 fibonacci numbers
def sumFib(N):

    # Apply the formula
    num = round(pow((pow(5,1/2) + 1) \
                    / 2.0, N + 2) \
                / pow(5,1/2));

    # Print the result
    print(num - 1);

# Driver Code
if __name__ == '__main__':
    N = 3;
    sumFib(N);

# This code is contributed by 29AjayKumar

C#

// C# program for the above approach
using System;
class GFG
{

    // Function to find the sum of
    // first N + 1 fibonacci numbers
    public static void sumFib(int N)
    {
        // Apply the formula
        long num = (long)Math.Round(
            Math.Pow((Math.Sqrt(5) + 1)
                         / 2.0,
                     N + 2)
            / Math.Sqrt(5));

        // Print the result
        Console.WriteLine(num - 1);
    }

// Driver Code
static public void Main()
{
        int N = 3;
        sumFib(N);
}
}

// This code is contributed by jana_sayantan.

Javascript

<script>

// Javascript program for the above approach

    // Function to find the sum of
    // first N + 1 fibonacci numbers
    function sumFib(N)
    {
        // Apply the formula
        var num =  Math.round(Math.pow((Math.sqrt(5) + 1)
        / 2.0, N + 2) / Math.sqrt(5));

        // Print the result
        document.write(num - 1);
    }

    // Driver Code

        var N = 3;
        sumFib(N);

// This code contributed by umadevi9616

</script>

Output:

4

Time Complexity: O(log n)
Auxiliary Space: O(1)

Alternate Approach: Follow the steps below to solve the problem:

• The N^th Fibonacci number can also be calculated using the generating function.
• The generating function for the N^th Fibonacci number is given by:

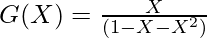
• Therefore, the generating function of the sum of Fibonacci numbers is given by:

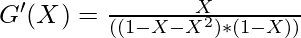
• After partial fraction decomposition of G'(X), the value of G'(X) is given by:

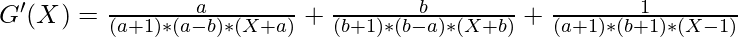
where, 

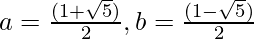
• Therefore, the formula for the sum of the Fibonacci numbers is given by:

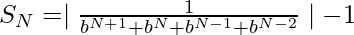
Below is the implementation of the above approach:

C++

// C++  program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to find the sum of
// first N + 1 fibonacci numbers
void sumFib(int N)
{

  // Apply the formula
  double num = (1 - sqrt(5)) / 2;

  long val = round(
    abs(1
        / (pow(num, N + 2)
           + pow(num, N + 1)
           + pow(num, N)
           + pow(num, N - 1)))
    - 1);

  // Print the result
  cout<<val;
}

// Driver Code
int main()
{
    int N = 3;

      // Function Call
    sumFib(N);
}

// This code is contributed by 29AjayKumar

Java

// Java program for the above approach
import java.io.*;

class GFG {

    // Function to find the sum of
    // first N + 1 fibonacci numbers
    public static void sumFib(int N)
    {
        // Apply the formula
        double num = (1 - Math.sqrt(5)) / 2;

        long val = Math.round(
            Math.abs(1
                     / (Math.pow(num, N + 2)
                        + Math.pow(num, N + 1)
                        + Math.pow(num, N)
                        + Math.pow(num, N - 1)))
            - 1);

        // Print the result
        System.out.println(val);
    }

    // Driver Code
    public static void main(String[] args)
    {
        int N = 3;

        // Function Call
        sumFib(N);
    }
}

Python3

# Python3 program for the above approach
import math

# Function to find the sum of
# first N + 1 fibonacci numbers
def sumFib(N):

    # Apply the formula
    num = (1 - math.sqrt(5)) / 2

    val = round(abs(1 / (pow(num, N + 2) +
                         pow(num, N + 1) +
                         pow(num, N) +
                         pow(num, N - 1))) - 1)

    # Print the result
    print(val)

# Driver Code
if __name__ == '__main__':

    N = 3

    # Function Call
    sumFib(N)

# This code is contributed by Surbhi Tyagi.

C#

// C# program for the above approach


using System;

public class GFG {

    // Function to find the sum of
    // first N + 1 fibonacci numbers
    public static void sumFib(int N)
    {
        // Apply the formula
        double num = (1 - Math.Sqrt(5)) / 2;

        double val = Math.Round(
            Math.Abs(1
                     / (Math.Pow(num, N + 2)
                        + Math.Pow(num, N + 1)
                        + Math.Pow(num, N)
                        + Math.Pow(num, N - 1)))
            - 1);

        // Print the result
        Console.WriteLine(val);
    }

    // Driver Code
    public static void Main(String[] args)
    {
        int N = 3;

        // Function Call
        sumFib(N);
    }
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// Javascript program for the above approach

    // Function to find the sum of
    // first N + 1 fibonacci numbers
    function sumFib(N) {
        // Apply the formula
        var num = ((1 - Math.sqrt(5)) / 2);

        var val = Math.round(
            Math.abs(1
                     / (Math.pow(num, N + 2)
                        + Math.pow(num, N + 1)
                        + Math.pow(num, N)
                        + Math.pow(num, N - 1)))
            - 1);

        // Print the result
        document.write(val);
    }

    // Driver Code

        var N = 3;

        // Function Call
        sumFib(N);

// This code is contributed by todaysgaurav

</script>

Output:

4

Time Complexity: O(log n)
Auxiliary Space: O(1)