Sum of cost of all paths to reach a given cell in a Matrix

Given a matrix grid[][] and two integers M and N, the task is to find the sum of cost of all possible paths from the (0, 0) to (M, N) by moving a cell down or right. Cost of each path is defined as the sum of values of the cells visited in the path.
Examples:

Input: M = 1, N = 1, grid[][] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}} 
Output: 18 
Explanation:
There are only 2 ways to reach (1, 1) 
Path 1: (0, 0) => (0, 1) => (1, 1) 
Path cost = 1 + 2 + 5 = 8 
Path 2: (0, 0) => (1, 0) => (1, 1) 
Path cost = 1 + 4 + 5 = 10 
Total Path Sum = 8 + 10 = 18
Input: M = 2, N = 2, grid = { {1, 1, 1}, {1, 1, 1}, {1, 1, 1} } 
Output: 30 
Explanation:
Sum of path cost of all path is 30. 

Approach: The idea is to find the contribution of each cell of the matrix for reaching (M, N), that is, the contribution of the every i and j, where 0 <= i <= M and 0 <= j <= N. 
Below is the illustration of the contribution of each cell to all paths from (0, 0) to (M, N) through the respective cells:

Number of ways to reach (M, N) from (0, 0) =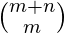 
Number of ways to reach (M, N) from (0, 0) via (i, j) =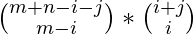 
Therefore, Contribution of each grid (i, j) is = 

Below is the implementation of the above approach:

C++

// C++ implementation to find the
// sum of cost of all paths
// to reach (M, N)

#include <iostream>
using namespace std;

const int Col = 3;
int fact(int n);

// Function for computing
// combination
int nCr(int n, int r)
{
    return fact(n) / (fact(r)
                      * fact(n - r));
}

// Function to find the
// factorial of N
int fact(int n)
{
    int res = 1;

    // Loop to find the factorial
    // of a given number
    for (int i = 2; i <= n; i++)
        res = res * i;
    return res;
}

// Function for coumputing the
// sum of all path cost
int sumPathCost(int grid[][Col],
                int m, int n)
{
    int sum = 0, count;

    // Loop to find the contribution
    // of each (i, j) in the all possible
    // ways
    for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= n; j++) {

            // Count number of
            // times (i, j) visited
            count
                = nCr(i + j, i)
                  * nCr(m + n - i - j, m - i);

            // Add the contribution of
            // grid[i][j] in the result
            sum += count * grid[i][j];
        }
    }
    return sum;
}

// Driver Code
int main()
{

    int m = 2;
    int n = 2;
    int grid[][Col] = { { 1, 2, 3 },
                        { 4, 5, 6 },
                        { 7, 8, 9 } };

    // Function Call
    cout << sumPathCost(grid, m, n);
    return 0;
}

Java

// Java implementation to find the
// sum of cost of all paths
// to reach (M, N)
import java.util.*;

class GFG{

static int Col = 3;

// Function for computing
// combination
static int nCr(int n, int r)
{
    return fact(n) / (fact(r) *
                      fact(n - r));
}

// Function to find the
// factorial of N
static int fact(int n)
{
    int res = 1;

    // Loop to find the factorial
    // of a given number
    for(int i = 2; i <= n; i++)
       res = res * i;
    return res;
}

// Function for coumputing the
// sum of all path cost
static int sumPathCost(int grid[][],
                       int m, int n)
{
    int sum = 0, count;

    // Loop to find the contribution
    // of each (i, j) in the all possible
    // ways
    for(int i = 0; i <= m; i++)
    {
       for(int j = 0; j <= n; j++)
       {

          // Count number of
          // times (i, j) visited
          count = nCr(i + j, i) *
                  nCr(m + n - i - j, m - i);

          // Add the contribution of
          // grid[i][j] in the result
          sum += count * grid[i][j];
       }
    }
    return sum;
}

// Driver code
public static void main(String[] args)
{
    int m = 2;
    int n = 2;
    int grid[][] = { { 1, 2, 3 },
                     { 4, 5, 6 },
                     { 7, 8, 9 } };

    // Function Call
    System.out.println(sumPathCost(grid, m, n));
}
}

// This code is contributed by offbeat

Python3

# Python3 implementation to find the sum
# of cost of all paths to reach (M, N)

Col = 3;

# Function for computing
# combination
def nCr(n, r):

    return fact(n) / (fact(r) *
                      fact(n - r));

# Function to find the
# factorial of N
def fact(n):

    res = 1;

    # Loop to find the factorial
    # of a given number
    for i in range(2, n + 1):
        res = res * i;
    return res;

# Function for coumputing the
# sum of all path cost
def sumPathCost(grid, m, n):

    sum = 0;
    count = 0;

    # Loop to find the contribution
    # of each (i, j) in the all possible
    # ways
    for i in range(0, m + 1):
        for j in range(0, n + 1):

            # Count number of
            # times (i, j) visited
            count = (nCr(i + j, i) *
                     nCr(m + n - i - j, m - i));

            # Add the contribution of
            # grid[i][j] in the result
            sum += count * grid[i][j];

    return sum;

# Driver code
if __name__ == '__main__':

    m = 2;
    n = 2;
    grid = [ [ 1, 2, 3 ],
             [ 4, 5, 6 ],
             [ 7, 8, 9 ] ];

    # Function Call
    print(int(sumPathCost(grid, m, n)));

# This code is contributed by 29AjayKumar

C#

// C# implementation to find the
// sum of cost of all paths
// to reach (M, N)
using System;

class GFG{

// Function for computing
// combination
static int nCr(int n, int r)
{
    return fact(n) / (fact(r) *
                      fact(n - r));
}

// Function to find the
// factorial of N
static int fact(int n)
{
    int res = 1;

    // Loop to find the factorial
    // of a given number
    for(int i = 2; i <= n; i++)
       res = res * i;
    return res;
}

// Function for coumputing the
// sum of all path cost
static int sumPathCost(int [,]grid,
                       int m, int n)
{
    int sum = 0, count;

    // Loop to find the contribution
    // of each (i, j) in the all possible
    // ways
    for(int i = 0; i <= m; i++)
    {
       for(int j = 0; j <= n; j++)
       {

          // Count number of
          // times (i, j) visited
          count = nCr(i + j, i) *
                  nCr(m + n - i - j, m - i);

          // Add the contribution of
          // grid[i][j] in the result
          sum += count * grid[i, j];
       }
    }
    return sum;
}

// Driver code
public static void Main()
{
    int m = 2;
    int n = 2;
    int [, ]grid = { { 1, 2, 3 },
                     { 4, 5, 6 },
                     { 7, 8, 9 } };

    // Function Call
    Console.Write(sumPathCost(grid, m, n));
}
}

// This code is contributed by Code_Mech

Javascript

<script>

// Javascript implementation to find the
// sum of cost of all paths
// to reach (M, N)

var Col = 3;

// Function for computing
// combination
function nCr(n, r)
{
    return fact(n) / (fact(r)
                      * fact(n - r));
}

// Function to find the
// factorial of N
function fact(n)
{
    var res = 1;

    // Loop to find the factorial
    // of a given number
    for (var i = 2; i <= n; i++)
        res = res * i;
    return res;
}

// Function for coumputing the
// sum of all path cost
function sumPathCost(grid, m, n)
{
    var sum = 0, count;

    // Loop to find the contribution
    // of each (i, j) in the all possible
    // ways
    for (var i = 0; i <= m; i++) {
        for (var j = 0; j <= n; j++) {

            // Count number of
            // times (i, j) visited
            count
                = nCr(i + j, i)
                  * nCr(m + n - i - j, m - i);

            // Add the contribution of
            // grid[i][j] in the result
            sum += count * grid[i][j];
        }
    }
    return sum;
}

// Driver Code
var m = 2;
var n = 2;
var grid = [ [ 1, 2, 3 ],
                    [ 4, 5, 6 ],
                    [ 7, 8, 9 ] ];
// Function Call
document.write( sumPathCost(grid, m, n));


</script>

Output:

150