Sum of Area of all possible square inside a rectangle

Given two integers L and B denoting the length and breadth of a rectangle respectively. The task is to calculate the sum of the area of all possible squares that comes into the rectangle.

Examples: 

Input: L = 4, B = 3
Output: 54

Input:  L = 2, B = 5
Output: 26

The idea is to observe the count of number of squares in a rectangle.  

Now, the number of squares of side 1 will be 12 as there will be two cases one as squares of 1-unit sides along the horizontal(3) and second case as squares of 1-unit sides along the vertical(4). That gives us 3*4 = 12 squares.

When the side is 2 units, one case will be as squares of side of 2 units along only one place horizontally and second case as two places vertically. So the number of squares = 6
So we can deduce that, 
Number of squares of size 1*1 will be L*B
Number of squares of size 2*2 will be (L-1)(B-1)
Therefore, the number of squares with size 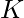will be: 

Number of square of size K = (L-K+1)*(B-K+1)

Therefore, area of total number of squares of size K will be: 

Area of total number of square of size K = (L-K+1)*(B-K+1)*K*K

Below is the implementation of above idea:

C++

// CPP program to calculate the sum of area
// of all possible squares that comes
// inside the rectangle

#include <bits/stdc++.h>
using namespace std;

// Function to calculate the sum of area
// of all possible squares that comes
// inside the rectangle
int calculateAreaSum(int l, int b)
{
    int size = 1;

    // Square with max size possible
    int maxSize = min(l,b);

    int totalArea = 0;

    for(int i=1; i <= maxSize; i++)
    {
        // calculate total square of a given size
        int totalSquares = (l-size+1)*(b-size+1);

        // calculate area of squares of a
        // particular size
        int area = totalSquares*size*size;

        // total area
        totalArea += area;

        // increment size
        size++;
    }

    return totalArea;
}

// Driver Code
int main()
{
    int l = 4, b = 3;

    cout<<calculateAreaSum(l,b);

    return 0;
}

Java

// Java program to calculate the
// sum of area of all possible
// squares that comes inside
// the rectangle
class GFG
{
// Function to calculate the
// sum of area of all possible
// squares that comes inside
// the rectangle
static int calculateAreaSum(int l, int b)
{
    int size = 1;

    // Square with max size possible
    int maxSize = Math.min(l, b);

    int totalArea = 0;

    for(int i = 1; i <= maxSize; i++)
    {
        // calculate total square
        // of a given size
        int totalSquares = (l - size + 1) *
                           (b - size + 1);

        // calculate area of squares
        // of a particular size
        int area = totalSquares *
                    size * size;

        // total area
        totalArea += area;

        // increment size
        size++;
    }

    return totalArea;
}

// Driver Code
public static void main(String[] args)
{
    int l = 4, b = 3;

    System.out.println(calculateAreaSum(l, b));
}
}

// This code is contributed
// by ChitraNayal

Python 3

# Python 3 program to calculate
# the sum of area of all possible
# squares that comes inside
# the rectangle

# Function to calculate the
# sum of area of all possible
# squares that comes inside
# the rectangle
def calculateAreaSum(l, b):
    size = 1

    # Square with max size possible
    maxSize = min(l, b)

    totalArea = 0

    for i in range(1, maxSize + 1 ):

        # calculate total square
        # of a given size
        totalSquares = ((l - size + 1) *
                        (b - size + 1))

        # calculate area of squares
        # of a particular size
        area = (totalSquares *
                size * size)

        # total area
        totalArea += area

        # increment size
        size += 1

    return totalArea

# Driver Code
if __name__ == "__main__":
    l = 4
    b = 3

    print(calculateAreaSum(l,b))

# This code is contributed
# by ChitraNayal

C#

// C# program to calculate the
// sum of area of all possible
// squares that comes inside
// the rectangle
using System;

class GFG
{
// Function to calculate the
// sum of area of all possible
// squares that comes inside
// the rectangle
static int calculateAreaSum(int l,
                            int b)
{
    int size = 1;

    // Square with max size possible
    int maxSize = Math.Min(l, b);

    int totalArea = 0;

    for(int i = 1; i <= maxSize; i++)
    {
        // calculate total square
        // of a given size
        int totalSquares = (l - size + 1) *
                           (b - size + 1);

        // calculate area of squares
        // of a particular size
        int area = totalSquares *
                   size * size;

        // total area
        totalArea += area;

        // increment size
        size++;
    }
    return totalArea;
}

// Driver Code
public static void Main()
{
    int l = 4, b = 3;

    Console.Write(calculateAreaSum(l,b));
}
}

// This code is contributed
// by ChitraNayal

PHP

<?php
// PHP program to calculate the
// sum of area of all possible
// squares that comes inside
// the rectangle

// Function to calculate the
// sum of area of all possible
// squares that comes inside
// the rectangle
function calculateAreaSum($l, $b)
{
    $size = 1;

    // Square with max size possible
    $maxSize = min($l, $b);

    $totalArea = 0;

    for($i = 1; $i <= $maxSize; $i++)
    {
        // calculate total square
        // of a given size
        $totalSquares = ($l - $size + 1) *
                        ($b - $size + 1);

        // calculate area of squares
        // of a particular size
        $area = $totalSquares *
                 $size * $size;

        // total area
        $totalArea += $area;

        // increment size
        $size++;
    }

    return $totalArea;
}

// Driver Code
$l = 4;
$b = 3;

echo calculateAreaSum($l,$b);

// This code is contributed
// by ChitraNayal
?>

Javascript

<script>

// Javascript program to calculate the sum of area
// of all possible squares that comes
// inside the rectangle

// Function to calculate the sum of area
// of all possible squares that comes
// inside the rectangle
function calculateAreaSum(l, b)
{
    var size = 1;

    // Square with max size possible
    var maxSize = Math.min(l,b);

    var totalArea = 0;

    for(var i=1; i <= maxSize; i++)
    {
        // calculate total square of a given size
        var totalSquares = (l-size+1)*(b-size+1);

        // calculate area of squares of a
        // particular size
        var area = totalSquares*size*size;

        // total area
        totalArea += area;

        // increment size
        size++;
    }

    return totalArea;
}

// Driver Code
var l = 4, b = 3;
document.write( calculateAreaSum(l,b));

// This code is contributed by noob2000.
</script>

Output

54

Complexity Analysis:

• Time complexity: O(min(l,b))
• Auxiliary complexity: O(1)