Sum of Angles in a Polygon

Polygon is defined as a two-dimensional geometric figure that has a finite number of line segments connected to form a closed shape. The line segments of a polygon are called edges or sides, and the point of intersection of two edges is called a vertex. The angle of a polygon is referred to as the space formed at the intersection point (vertex) of two adjacent sides.

A polygon is of two types: a regular polygon and an irregular polygon. A regular polygon is a polygon whose all sides and all interior angles are measured the same, whereas an irregular polygon is a polygon whose all sides and all interior angles do not measure the same. And we also have different types of polygons like triangles, quadrilaterals, pentagons, hexagons, etc, based on the number of sides of a polygon. Every polygon has interior angles and exterior angles, where an interior angle is the one that lies inside the polygon and the exterior angle is the one that lies outside the polygon.

Angles in Polygons

Angles in polygons are the angles formed by the intersection of two adjacent sides of the polygon. There are two main types of angles associated with polygons: interior angles and exterior angles.

Interior Angles

The angle of a polygon is referred to as the space formed at the intersection point (vertex) of two adjacent sides. Now, the interior angle of a polygon is the one that lies inside the polygon. The number of angles in a polygon having “n” sides is “n”. For example, a triangle has three sides, so it has three interior angles.

We know that a polygon is of two types of the polygon: a regular polygon and an irregular polygon. The measurement of all interior angles is the same, whereas in an irregular polygon the measurement of each angle may differ. In the figure given below, ABCD is a square whose interior angles are ∠1, ∠2, ∠3, and ∠4.

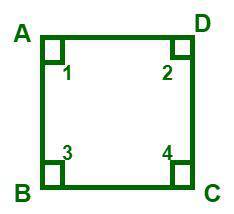
Square

Exterior Angles

The angle that lies at the outside of a polygon, which is formed by one side of the polygon and the extension of the other side, is referred to as the exterior angle of a polygon. The sum of an adjacent interior angle and exterior angle is equal to 180°. And the sum of all the exterior angles of a polygon is always equal to 360°.

Exterior angle of a regular polygon = 360° ÷ number of sides = 360°/n

Exterior angles of a pentagon

Sum of Interior Angles of a Polygon

Every polygon has interior angles and exterior angles, where an interior angle is the one that lies inside the polygon and the exterior angle is the one that lies outside the polygon. The number of angles and their measurements differ from one polygon to another based on the number of sides of a polygon.

For example, a triangle has three interior angles, and its sum is equal to 180°, whereas a square has four interior angles, and its sum is equal to 360°. But the sum of the interior angles of a polygon remains the same whether it is a regular or an irregular polygon.

The formula to determine the sum of the interior angles of a polygon is given as follows:

S = (n – 2) × 180°

Where,

• S is the sum of interior angles, and
• n is the number of sides or number of angles of polygons

Interior Angle Formulae

The interior angle of a polygon is the one that lies inside the polygon. The interior angle of a polygon can be found in the following ways:

Using the Number of Sides

The measure of each interior angle of a regular polygon having n sides is given as follows:

I = [(n – 2) × 180° / n]

Where,

• I is the value of the interior angle, and
• n is the number of sides or number of angles of polygons.

Using Exterior Angle

We know that the sum of an adjacent interior angle and exterior angle is equal to 180°. So, when the exterior angle of a polygon is given, the polygon formula to determine the interior angle of a polygon is given as follows:

I = 180° – E

Where,

• I is the value of the interior angle, and
• E is the corresponding exterior angle for that interior angle.

Using Sum of Interior Angles

We know that all the interior angles of a regular polygon are equal. So, the measure of each interior angle of a regular polygon is equal to the sum of the interior angles of the polygon divided by the number of sides.

I = S / n

Where,

• S is the sum of interior angles, and
• n is the number of sides or number of angles of polygons

Interior Angles of Regular Polygons

Interior angles of first 10 regular polygons are listed in the following table:

Name of the polygon	Number of sides (n)	Sum of interior angles S = (n – 2) × 180°	Measurement of each interior angle of a regular polygon [(n – 2) × 180°/n]
Triangle	3	180°	180/3 = 60°
Quadrilateral	4	360°	360/4 = 90°
Pentagon	5	540°	540/5 = 108°
Hexagon	6	720°	720/6 = 120°
Heptagon	7	900°	900/7 = 128.57°
Octagon	8	1080°	1080/8 = 135°
Nonagon	9	1260°	1260/9 = 140°
Decagon	10	1440°	1440/10 = 144°

Sum of Interior Angle of  Polygon Theorem

Statement: The interior angle theorem states the sum of the interior angles of a polygon with n vertices is S = (n – 2) × 180°.

Derivation:

To prove the interior angle theorem, we need the statement that the sum of the interior angles of a triangle is 180°.

Now, let us consider a polygon having “n” sides. A polygon having “n” sides forms “n” triangles. For example, look at the figure given below, where a polygon having 8 sides has formed 8 triangles.

As we know that the sum of the interior angles of a triangle is 180°, the sum of all the interior angles of “n” triangles will be n × 180°.

Sum of all the interior angles of “n” triangles = n × 180°

So, we can conclude that,

Sum of interior angles of the polygon + Sum of the angles at the point O = n × 180° ——— (1)

We know that the sum of the angles at the point O = 360° ——— (2)

By substituting equation (2) in equation (1), we get

Sum of interior angles of the polygon + 360°= n × 180°

So, the sum of interior angles of the polygon = n × 180° – 360°

= (n – 2) × 180° 

Thus, the sum of interior angles of the polygon = (n – 2) × 180°

The measure of each interior angle of a regular polygon = ((n – 2) × 180°/n) (Since the measure of each angle is the same for a regular polygon)

Hence proved.

Related Resources

• Area of Triangle
• Area of Square
• Area of Rectangle

Solved Examples on Interior Angles Formula

Example 1: Determine the sum of interior angles of a regular heptagon.

Solution: 

We know that a heptagon has seven sides, i.e., n = 7.

From the sum of the interior angles of a given polygon,

We have, S = (n − 2) × 180°

= (7 − 2) × 180°

= 5 × 180° = 900°

Hence, the sum of interior angles of a regular heptagon is 900°.

Example 2: Find the interior angle at vertex C in the figure given below.

Solution:

The given polygon is a pentagon. We know that a pentagon has seven sides, i.e., n = 5.

From the sum of the interior angles of a given polygon,

We have, S = (n − 2) × 180°

= (5 − 2) × 180° = 540°

Now, we have the sum of all the interior angles in the given polygon is 540°.

∠A + ∠B + ∠C + ∠D + ∠E = 540°

x + 111° + (x – 20°) + 105° + (x – 10°) = 540°

3x + 186° = 540°

3x = 354°

x = 118°

Now, let the angle at ∠C = x – 20°

= 118° – 20°

∠C = 98°

Thus, the interior angle at vertex C is ∠C = 98°.

Example 3: What is the sum of the interior angles of a polygon having 12 sides?

Solution: 

Given data:

The number of sides of the given polygon (n) = 12

From the sum of the interior angles of a given polygon,

We have, S = (n − 2) × 180°

= (12 − 2) × 180°

= 10 × 180° = 1800°

The sum of interior angles of a polygon having 12 sides is equal to 1800°.

Example 4: What is the measure of the interior angles of a regular polygon having 8 sides?

Solution:

Given data:

The number of sides of the given polygon (n) = 8

Since the given polygon is regular, all the angles are equal.

We have,

The measure of each interior angle of a regular polygon = (n – 2) × 180°/n

= [(8 − 2) × 180°]/8

= 1,080°/8 = 135°

Hence, the measure of each interior angle of a regular polygon having 8 sides is 135°.

Example 5: Find the interior angle at vertex F in the figure given below.

Figure ABCDEF

Solution:

The given polygon is a pentagon. We know that a pentagon has seven sides, i.e., n = 5.

From the sum of the interior angles of a given polygon,

We have, S = (n − 2) × 180°

= (6 − 2) × 180° = 720°

Now, we have the sum of all the interior angles in the given polygon is 720°.

∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°

132° + y° + (y – 15)° + 110° + (y – 20)° + 99° = 720°

3y + 306° = 720°

3y = 414°

y = 138°

Now, let the angle at ∠F = y – 20°

= 138° – 20°

∠F = 118°

Thus, the interior angle at vertex F is ∠F = 118°.

FAQs on Interior Angles Formula

Define an interior angle of a polygon.

The angle of a polygon is referred to as the space formed at the intersection point (vertex) of two adjacent sides. Now, the interior angle of a polygon is the one that lies inside the polygon. The number of angles in a polygon having “n” sides is “n”. For example, a triangle has three sides, so it has three interior angles. 

What is the formula to determine the sum of the interior angles of a polygon?

The formula to determine the sum of interior angles of a polygon is given as follows:

Sum (S) = (n − 2) × 180°

where “n” is the number of sides or number of angles of polygons.

What is the sum of all interior angles of an octagon?

The sum of interior angles of an octagon is 1080°.

What is the sum of all interior angles of a triangle?

Sum of interior angles of a triangle is 180°.

Define an exterior angle of a polygon.

The angle that lies at the outside of a polygon, which is formed by one side of the polygon and the extension of the other side, is referred to as the exterior angle of a polygon.