Sum of all the prime numbers in a given range
Last Updated :
14 Sep, 2023
Given a range [l, r], the task is to find the sum of all the prime numbers within that range.
Examples:
Input : l=1 and r=6
Output : 10
Input : l=4 and r=13
Output : 36
Approach 1: (Naive Approach)
Iterate the loop from ‘l’ to ‘r’ and add all the numbers which are prime.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
bool checkPrime(int numberToCheck)
{
if(numberToCheck == 1) {
return false;
}
for (int i = 2; i*i <= numberToCheck; i++) {
if (numberToCheck % i == 0) {
return false;
}
}
return true;
}
int primeSum(int l, int r)
{
int sum = 0;
for (int i = r; i >= l; i--) {
bool isPrime = checkPrime(i);
if (isPrime) {
sum = sum + i;
}
}
return sum;
}
int main()
{
int l = 4, r = 13;
cout << primeSum(l, r);
}
|
Java
public class GFG {
static boolean checkPrime(int numberToCheck)
{
if(numberToCheck == 1) {
return false;
}
for (int i = 2; i*i <= numberToCheck; i++) {
if (numberToCheck % i == 0) {
return false;
}
}
return true;
}
static int primeSum(int l, int r)
{
int sum = 0;
for (int i = r; i >= l; i--) {
boolean isPrime = checkPrime(i);
if (isPrime) {
sum = sum + i;
}
}
return sum;
}
public static void main(String[] args)
{
int l = 4, r = 13;
System.out.println(primeSum(l, r));
}
}
|
Python 3
from math import sqrt
def checkPrime(numberToCheck) :
if numberToCheck == 1 :
return False
for i in range(2, int(sqrt(numberToCheck)) + 1) :
if numberToCheck % i == 0 :
return False
return True
def primeSum(l, r) :
sum = 0
for i in range(r, (l - 1), -1) :
isPrime = checkPrime(i)
if (isPrime) :
sum += i
return sum
if __name__ == "__main__" :
l, r = 4, 13
print(primeSum(l, r))
|
C#
using System;
class GFG
{
static bool checkPrime(int numberToCheck)
{
if(numberToCheck == 1)
{
return false;
}
for (int i = 2;
i * i <= numberToCheck; i++)
{
if (numberToCheck % i == 0)
{
return false;
}
}
return true;
}
static int primeSum(int l, int r)
{
int sum = 0;
for (int i = r; i >= l; i--)
{
bool isPrime = checkPrime(i);
if (isPrime)
{
sum = sum + i;
}
}
return sum;
}
public static void Main()
{
int l = 4, r = 13;
Console.Write(primeSum(l, r));
}
}
|
Javascript
<script>
function checkPrime(numberToCheck)
{
if(numberToCheck == 1)
{
return false;
}
for (let i = 2; i * i <= numberToCheck; i++)
{
if (numberToCheck % i == 0)
{
return false;
}
}
return true;
}
function primeSum(l, r)
{
let sum = 0;
for (let i = r; i >= l; i--)
{
let isPrime = checkPrime(i);
if (isPrime)
{
sum = sum + i;
}
}
return sum;
}
let l = 4, r = 13;
document.write(primeSum(l, r));
</script>
|
PHP
<?php
function checkPrime($numberToCheck)
{
if($numberToCheck == 1)
{
return false;
}
for ($i = 2; $i * $i <= $numberToCheck; $i++)
{
if ($numberToCheck % $i == 0)
{
return false;
}
}
return true;
}
function primeSum($l, $r)
{
$sum = 0;
for ($i = $r; $i >= $l; $i--)
{
$isPrime = checkPrime($i);
if ($isPrime)
{
$sum = $sum + $i;
}
}
return $sum;
}
$l = 4; $r = 13;
echo primeSum($l, $r);
?>
|
Time Complexity: 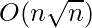
Auxiliary Space: 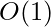
Approach 2: (Dynamic Programming)
- Declare an array dp and arr
- Fill the array arr to 0
- Iterate the loop till sqrt(N) and if arr[i] = 0 (marked as prime), then set all of its multiples as non-prime by marking the respective location as 1
- Update the dp array with the running prime numbers sum, where each location ‘dp[i]’ holds the sum of all the prime numbers within the range [1, i]
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int N = 1000;
int dp[N + 1];
void sieve()
{
int arr[N + 1]={0};
arr[0] = 1;
arr[1] = 1;
for (int i = 2; i <= sqrt(N); i++)
if (arr[i] == 0)
for (int j = i * i; j <= N; j += i)
arr[j] = 1;
long runningPrimeSum = 0;
for (int i = 1; i <= N; i++)
{
if (arr[i] == 0)
runningPrimeSum += i;
dp[i] = runningPrimeSum;
}
}
int main()
{
int l = 4, r = 13;
sieve();
cout << dp[r] - dp[l - 1];
return 0;
}
|
Java
public class GFG {
static int N = 1000;
static long dp[] = new long[N + 1];
static void sieve()
{
int arr[] = new int[N + 1];
arr[0] = 1;
arr[1] = 1;
for (int i = 2; i <= Math.sqrt(N); i++)
if (arr[i] == 0)
for (int j = i * i; j <= N; j += i)
arr[j] = 1;
long runningPrimeSum = 0;
for (int i = 1; i <= N; i++) {
if (arr[i] == 0)
runningPrimeSum += i;
dp[i] = runningPrimeSum;
}
}
public static void main(String[] args)
{
int l = 4, r = 13;
sieve();
System.out.println(dp[r] - dp[l - 1]);
}
}
|
Python 3
import math
N = 1000
dp = [0] * (N + 1)
def sieve():
array = [0] * (N + 1)
array[0] = 1
array[1] = 1
for i in range(2, math.ceil(math.sqrt(N) + 1)):
if array[i] == 0:
for j in range(i * i, N + 1, i):
array[j] = 1
runningPrimeSum = 0
for i in range(1, N + 1):
if array[i] == 0:
runningPrimeSum += i
dp[i] = runningPrimeSum
l = 4
r = 13
sieve()
print(dp[r] - dp[l - 1])
|
C#
using System;
public class GFG {
static int N = 1000;
static long[] dp = new long[N + 1];
static void sieve()
{
int []arr = new int[N + 1];
arr[0] = 1;
arr[1] = 1;
for (int i = 2; i <= Math.Sqrt(N); i++)
if (arr[i] == 0)
for (int j = i * i; j <= N; j += i)
arr[j] = 1;
long runningPrimeSum = 0;
for (int i = 1; i <= N; i++) {
if (arr[i] == 0)
runningPrimeSum += i;
dp[i] = runningPrimeSum;
}
}
public static void Main()
{
int l = 4, r = 13;
sieve();
Console.WriteLine(dp[r] - dp[l - 1]);
}
}
|
Javascript
<script>
let N = 1000;
let dp=new Array(N+1);
for(let i=0;i<dp.length;i++)
{
dp[i]=0;
}
function sieve()
{
let arr=new Array(N+1);
for(let i=0;i<arr.length;i++)
{
arr[i]=0;
}
arr[0] = 1;
arr[1] = 1;
for (let i = 2; i <= Math.ceil(Math.sqrt(N)+1); i++)
if (arr[i] == 0)
for (let j = i * i; j <= N; j += i)
arr[j] = 1;
let runningPrimeSum = 0;
for (let i = 1; i <= N; i++) {
if (arr[i] == 0)
runningPrimeSum += i;
dp[i] = runningPrimeSum;
}
}
let l = 4, r = 13;
sieve();
document.write(dp[r] - dp[l - 1]);
</script>
|
Time Complexity: O(n*log(log(n)))
Auxiliary Space: 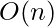
New Approach:- (Approach 3) Optimized Sieve of Eratosthenes
The Sieve of Eratosthenes is an efficient algorithm for finding all prime numbers up to a given limit. We can modify this algorithm to solve the problem of finding the sum of prime numbers in a given range.
Below is the implementation of the above approach:
C++
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int primeSum(int l, int r) {
vector<bool> isPrime(r + 1, true);
isPrime[0] = isPrime[1] = false;
for (int i = 2; i <= sqrt(r); i++) {
if (isPrime[i]) {
for (int j = i * i; j <= r; j += i) {
isPrime[j] = false;
}
}
}
int sum = 0;
for (int i = l; i <= r; i++) {
if (isPrime[i]) {
sum += i;
}
}
return sum;
}
int main() {
int l = 4, r = 13;
cout << primeSum(l, r) << endl;
return 0;
}
|
Java
import java.util.Arrays;
public class Main {
static int primeSum(int l, int r)
{
boolean[] isPrime = new boolean[r + 1];
Arrays.fill(isPrime, true);
isPrime[0] = isPrime[1] = false;
for (int i = 2; i <= Math.sqrt(r); i++) {
if (isPrime[i]) {
for (int j = i * i; j <= r; j += i) {
isPrime[j] = false;
}
}
}
int sum = 0;
for (int i = l; i <= r; i++) {
if (isPrime[i]) {
sum += i;
}
}
return sum;
}
public static void main(String[] args)
{
int l = 4, r = 13;
System.out.println(primeSum(l, r));
}
}
|
Python3
import math
def primeSum(l, r):
isPrime = [True] * (r + 1)
isPrime[0] = isPrime[1] = False
for i in range(2, math.isqrt(r) + 1):
if isPrime[i]:
for j in range(i * i, r + 1, i):
isPrime[j] = False
primeSum = 0
for i in range(l, r + 1):
if isPrime[i]:
primeSum += i
return primeSum
l = 4
r = 13
print(primeSum(l, r))
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int PrimeSum(int l, int r)
{
bool[] isPrime = new bool[r + 1];
for (int i = 2; i <= r; i++) {
isPrime[i] = true;
}
for (int i = 2; i <= Math.Sqrt(r); i++) {
if (isPrime[i]) {
for (int j = i * i; j <= r; j += i) {
isPrime[j] = false;
}
}
}
int sum = 0;
for (int i = l; i <= r; i++) {
if (isPrime[i]) {
sum += i;
}
}
return sum;
}
static void Main()
{
int l = 4, r = 13;
int sum = PrimeSum(l, r);
Console.WriteLine(sum);
}
}
|
Javascript
function primeSum(l, r) {
let isPrime = new Array(r + 1).fill(true);
isPrime[0] = isPrime[1] = false;
for (let i = 2; i <= Math.sqrt(r); i++) {
if (isPrime[i]) {
for (let j = i * i; j <= r; j += i) {
isPrime[j] = false;
}
}
}
let sum = 0;
for (let i = l; i <= r; i++) {
if (isPrime[i]) {
sum += i;
}
}
return sum;
}
let l = 4, r = 13;
console.log(primeSum(l, r));
|
Time complexity: O(r log log r).
Auxiliary Space: O(r)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...