Sum of all subsequences of length K

Difficulty Level : Hard
Last Updated : 04 May, 2021

Given an array arr[]and an integer K, the task is to find the sum of all K length subsequences from the given array.

Example:

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

Input: arr[] = {2, 3, 4}, K = 2
Output: 18
Explanation:
There are 3 possible subsequences of length 2 which are {2, 3}, {2, 4} and {3, 4}
The sum of all 2 length subsequences is 5 + 6 + 7 = 18

Input: arr[] = {7, 8, 9, 2}, K = 2
Output: 78
Explanation:
There are 6 subsequences of length 2 which are {7, 8}, {7, 9}, {7, 2}, {8, 9}, {8, 2} and {9, 2}.
The sum of all 2 length sub sequences is 15 + 16 + 9 + 17 + 10 + 11 = 78

Approach:
To solve the problem mentioned above we have to consider all K length subsequence that is “n choose k”, i.e. 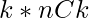$k * nCk$

The count of total element in all K length subsequences is 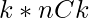$k * nCk$ , possibility of appearing of each element is same.
So each element appears 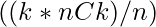$((k * nCk) / n )$ times and it contributes $arr[i] * ( (k*nCk)/n )$ in the result.
Hence, the sum of all K length subsequence is $sum(array) * ( (k * nCk) / n )$

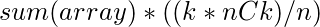
Below is the implementation of the above mentioned approach:

C++

// C++ implementation to find sum
// of all subsequences of length K
  
#include <bits/stdc++.h>
using namespace std;
  
int fact(int n);
  
// Function to find nCr
int nCr(int n, int r)
{
    return fact(n)
           / (fact(r)
              * fact(n - r));
}
  
// Function that returns
// factorial of n
int fact(int n)
{
    int res = 1;
    for (int i = 2; i <= n; i++)
        res = res * i;
    return res;
}
  
// Function for finding sum
// of all K length subsequences
int sumSubsequences(
    int arr[], int n, int k)
{
  
    int sum = 0;
  
    // Calculate the sum of array
    for (int i = 0; i < n; i++) {
        sum += arr[i];
    }
    int kLengthSubSequence;
  
    // Calculate nCk
    kLengthSubSequence = nCr(n, k);
  
    int ans
        = sum
          * ((k * kLengthSubSequence)
             / n);
  
    // Return the final result
    return ans;
}
  
// Driver code
int main()
{
  
    int arr[] = { 7, 8, 9, 2 };
  
    int K = 2;
  
    int n = sizeof(arr) / sizeof(arr[0]);
  
    cout << sumSubsequences(arr, n, K);
    return 0;
}

Java

// Java implementation to find sum
// of all subsequences of length K
class GFG{
  
// Function to find nCr
static int nCr(int n, int r)
{
    return fact(n) / (fact(r) * fact(n - r));
}
  
// Function that returns
// factorial of n
static int fact(int n)
{
    int res = 1;
    for (int i = 2; i <= n; i++)
        res = res * i;
    return res;
}
  
// Function for finding sum
// of all K length subsequences
static int sumSubsequences(int arr[], 
                           int n, int k)
{
    int sum = 0;
  
    // Calculate the sum of array
    for (int i = 0; i < n; i++) 
    {
        sum += arr[i];
    }
    int kLengthSubSequence;
  
    // Calculate nCk
    kLengthSubSequence = nCr(n, k);
  
    int ans = sum * ((k * kLengthSubSequence) / n);
  
    // Return the final result
    return ans;
}
  
// Driver code
public static void main(String[] args)
{
    int arr[] = { 7, 8, 9, 2 };
  
    int K = 2;
  
    int n = arr.length;
  
    System.out.print(sumSubsequences(arr, n, K));
}
}
  
// This code contributed by Rajput-Ji

Python3

# Python3 implementation to find sum 
# of all subsequences of length K
  
# Function to find nCr 
def nCr(n, r):
      
    return fact(n) / (fact(r) * 
                      fact(n - r))
  
# Function that returns 
# factorial of n
def fact(n):
      
    res = 1
    for i in range(2, n + 1):
        res = res * i 
    return res
      
# Function for finding sum 
# of all K length subsequences
def sumSubsequences(arr, n, k):
      
    sum = 0
      
    # Calculate the sum of array 
    for i in range(0, n):
        sum = sum + arr[i]
      
    # Calculate nCk     
    kLengthSubSequence = nCr(n, k)
    ans = sum * ((k * kLengthSubSequence) / n);
      
    # Return the final result 
    return ans
  
# Driver Code 
arr = [ 7, 8, 9, 2 ]
k = 2
n = len(arr)
  
print(sumSubsequences(arr, n, k))
  
# This code is contributed by skylags    

C#

// C# implementation to find sum
// of all subsequences of length K
using System;
  
class GFG{
      
// Function to find nCr
static int nCr(int n, int r)
{
    return fact(n) / (fact(r) * fact(n - r));
}
      
// Function that returns
// factorial of n
static int fact(int n)
{
    int res = 1;
      
    for(int i = 2; i <= n; i++)
       res = res * i;
    return res;
}
      
// Function for finding sum
// of all K length subsequences
static int sumSubsequences(int[] arr, 
                           int n, int k)
{
    int sum = 0;
      
    // Calculate the sum of array
    for(int i = 0; i < n; i++) 
    {
       sum += arr[i];
    }
      
    int kLengthSubSequence;
      
    // Calculate nCk
    kLengthSubSequence = nCr(n, k);
    int ans = sum * ((k * kLengthSubSequence) / n);
      
    // Return the final result
    return ans;
}
  
// Driver code
static void Main() 
{
    int[] arr = { 7, 8, 9, 2 };
    int K = 2;
    int n = arr.Length;
          
    Console.Write(sumSubsequences(arr, n, K));
}
}
  
// This code is contributed by divyeshrabadiya07

Javascript

<script>
  
// Javascript implementation to find sum
// of all subsequences of length K
  
// Function to find nCr
function nCr(n, r)
{
    return fact(n) / (fact(r) * 
           fact(n - r));
}
  
// Function that returns
// factorial of n
function fact(n)
{
    var res = 1;
    for(var i = 2; i <= n; i++)
        res = res * i;
          
    return res;
}
  
// Function for finding sum
// of all K length subsequences
function sumSubsequences(arr, n, k)
{
    var sum = 0;
  
    // Calculate the sum of array
    for(var i = 0; i < n; i++)
    {
        sum += arr[i];
    }
    var kLengthSubSequence;
  
    // Calculate nCk
    kLengthSubSequence = nCr(n, k);
  
    var ans = sum * ((k * 
              kLengthSubSequence) / n);
  
    // Return the final result
    return ans;
}
  
// Driver code
var arr = [ 7, 8, 9, 2 ];
var K = 2;
var n = arr.length;
  
document.write(sumSubsequences(arr, n, K));
  
// This code is contributed by noob2000
  
</script>

Output:

My Personal Notes

Related Articles

Sum of all subsequences of length K

C++

Java

Python3

C#

Javascript