Sum of all N digit palindromic numbers divisible by 9 formed using digits 1 to 9
Last Updated :
29 Jul, 2022
Given a number N, the task is to find the sum of all N digits palindromic numbers (formed by digits from 1 to 9) that are divisible by 9. Examples:
Input: N = 1 Output: 9 Explanation: Only 9 is a palindromic number of 1 digit divisible by 9 Input: N = 3 Output: 4995 Explanation: Three-digit Palindromic Numbers divisible by 9 are – 171, 252, 333, 414, 585, 666, 747, 828, 999
Approach: The key observation in the problem is that if a number is divisible by 9, then the sum of digits of that number is also divisible by 9. Another observation is if we count the number of N-digit palindromic numbers using the digits from 1 to 9, then it can be observed that
Occurrence of each digit = (count of N-digit numbers / 9)
Therefore,
- First find the count of N-digit Palindromic numbers divisible by 9, as:
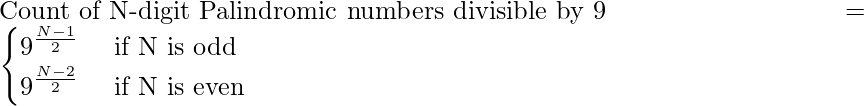
- Then if N is 1 or 2, the sum will be simply 9 and 99 respectively, as they are the only palindromic numbers of 1 and 2 digits.
- If N > 2, then the sum for Nth digit palindromic numbers divisible by 9 is \text{Sum of Nth digit palindromic numbers divisible by 9 }= (\text{sum of }(N-1)^{th}\text{ digit } * 10) + (5*\text{ count of N digit palindromic numbers divisible by 9})
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countPalindrome(int n)
{
int count;
if (n % 2 == 1) {
count = pow(9, (n - 1) / 2);
}
else {
count = pow(9, (n - 2) / 2);
}
return count;
}
int sumPalindrome(int n)
{
int count = countPalindrome(n);
int res = 0;
if (n == 1)
return 9;
if (n == 2)
return 99;
for (int i = 0; i < n; i++) {
res = res * 10 + count * 5;
}
return res;
}
int main()
{
int n = 3;
cout << sumPalindrome(n);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int countPalindrome(int n)
{
int count;
if (n % 2 == 1)
{
count = (int)Math.pow(9, (n - 1) / 2);
}
else
{
count = (int)Math.pow(9, (n - 2) / 2);
}
return count;
}
static int sumPalindrome(int n)
{
int count = countPalindrome(n);
int res = 0;
if (n == 1)
return 9;
if (n == 2)
return 99;
for(int i = 0; i < n; i++)
{
res = res * 10 + count * 5;
}
return res;
}
public static void main(String[] args)
{
int n = 3;
System.out.println(sumPalindrome(n));
}
}
|
Python3
def countPalindrome(n):
count = 0
if (n % 2 == 1):
count = pow(9, (n - 1) // 2)
else:
count = pow(9, (n - 2) // 2)
return count
def sumPalindrome(n):
count = countPalindrome(n)
res = 0
if (n == 1):
return 9
if (n == 2):
return 99
for i in range(n):
res = res * 10 + count * 5
return res
n = 3
print(sumPalindrome(n))
|
C#
using System;
class GFG{
static int countPalindrome(int n)
{
int count;
if (n % 2 == 1)
{
count = (int)Math.Pow(9, (n - 1) / 2);
}
else
{
count = (int)Math.Pow(9, (n - 2) / 2);
}
return count;
}
static int sumPalindrome(int n)
{
int count = countPalindrome(n);
int res = 0;
if (n == 1)
return 9;
if (n == 2)
return 99;
for(int i = 0; i < n; i++)
{
res = res * 10 + count * 5;
}
return res;
}
public static void Main(String[] args)
{
int n = 3;
Console.WriteLine(sumPalindrome(n));
}
}
|
Javascript
function countPalindrome(n)
{
let count;
if (n % 2 == 1) {
count = Math.pow(9, (n - 1) / 2);
}
else {
count = Math.pow(9, (n - 2) / 2);
}
return count;
}
function sumPalindrome(n)
{
let count = countPalindrome(n);
let res = 0;
if (n == 1)
return 9;
if (n == 2)
return 99;
for (var i = 0; i < n; i++) {
res = res * 10 + count * 5;
}
return res;
}
let n = 3;
console.log(sumPalindrome(n));
|
Output:
4995
Time Complexity: O(log9n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...