Given a positive integer n. Find the value of
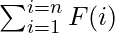
where function F(i) for number i be defined as the sum of all divisors of ‘i‘.
Examples :
Input: 4
Output: 15
Explanation
F(1) = 1
F(2) = 1 + 2 = 3
F(3) = 1 + 3 = 4
F(4) = 1 + 2 + 4 = 7
ans = F(1) + F(2) + F(3) + F(4)
= 1 + 3 + 4 + 7
= 15
Input: 5
Output: 21
Naive approach is to traverse for every number(1 to n), find all divisors and keep updating the sum with that divisor. See this to understand more.
C++
#include<bits/stdc++.h>
using namespace std;
int divisorSum(int n)
{
int sum = 0;
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j * j <= i; ++j)
{
if (i % j == 0)
{
if (i / j == j)
sum += j;
else
sum += j + i / j;
}
}
}
return sum;
}
int main()
{
int n = 4;
cout << " " << divisorSum(n) << endl;
n = 5;
cout << " " << divisorSum(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int divisorSum(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j * j <= i; ++j) {
if (i % j == 0) {
if (i / j == j)
sum += j;
else
sum += j + i / j;
}
}
}
return sum;
}
public static void main(String args[])
{
int n = 4;
System.out.println(divisorSum(n));
n = 5;
System.out.println(divisorSum(n));
}
}
|
Python3
def divisorSum( n ):
sum = 0
for i in range(1, n + 1):
j = 1
while j * j <= i:
if i % j == 0:
if i / j == j:
sum += j
else:
sum += j + i / j
j = j + 1
return int(sum)
n = 4
print( divisorSum(n))
n = 5
print( divisorSum(n))
|
C#
using System;
class GFG {
static int divisorSum(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j * j <= i; ++j) {
if (i % j == 0) {
if (i / j == j)
sum += j;
else
sum += j + i / j;
}
}
}
return sum;
}
public static void Main()
{
int n = 4;
Console.WriteLine(divisorSum(n));
n = 5;
Console.WriteLine(divisorSum(n));
}
}
|
Javascript
<script>
function divisorSum(n)
{
let sum = 0;
for (let i = 1; i <= n; ++i)
{
for (let j = 1; j * j <= i; ++j)
{
if (i % j == 0)
{
if (i / j == j)
sum += j;
else
sum += j + i / j;
}
}
}
return sum;
}
let n = 4;
document.write(divisorSum(n) + "<br>");
n = 5;
document.write(divisorSum(n) + "<br>");
</script>
|
PHP
<?php
function divisorSum($n)
{
$sum = 0;
for ($i = 1; $i <= $n; ++$i)
{
for ($j = 1; $j * $j <= $i; ++$j)
{
if ($i % $j == 0)
{
if ($i / $j == $j)
$sum += $j;
else
$sum += $j + $i / $j;
}
}
}
return $sum;
}
$n = 4;
echo "\n", divisorSum($n), "\n";
$n = 5;
echo divisorSum($n), "\n";
?>
|
Time complexity: O(n√(n)))
Auxiliary space: O(1)
Efficient approach is to observe the function and co-relate the pattern. For a given number n, every number from 1 to n contributes its presence up to the highest multiple less than n. For instance,
Let n = 6,
=> F(1) + F(2) + F(3) + F(4) + F(5) + F(6)
=> 1 will occurs 6 times in F(1), F(2),
F(3), F(4), F(5) and F(6)
=> 2 will occurs 3 times in F(2), F(4) and
F(6)
=> 3 will occur 2 times in F(3) and F(6)
=> 4 will occur 1 times in F(4)
=> 5 will occur 1 times in F(5)
=> 6 will occur 1 times in F(6)
From the above observation, it can easily be observed that number i is occurring only in their multiples less than or equal to n. Thus, we just need to find the count of multiples and then multiply it with i for full contribution in the final sum. It can easily be done in O(1) time by taking the floor of (n / i) and then multiply it with i for the sum.
C++
#include<bits/stdc++.h>
using namespace std;
int divisorSum(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
sum += (n / i) * i;
return sum;
}
int main()
{
int n = 4;
cout <<" "<< divisorSum(n)<<endl;
n = 5;
cout <<" "<< divisorSum(n)<< endl;
return 0;
}
|
C
#include <stdio.h>
int divisorSum(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
sum += (n / i) * i;
return sum;
}
int main()
{
int n = 4;
printf("%d\n", divisorSum(n));
n = 5;
printf("%d", divisorSum(n));
return 0;
}
|
Java
import java.io.*;
class GFG {
static int divisorSum(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
sum += (n / i) * i;
return sum;
}
public static void main(String args[])
{
int n = 4;
System.out.println(divisorSum(n));
n = 5;
System.out.println(divisorSum(n));
}
}
|
Python3
def divisorSum( n ):
sum = 0
for i in range(1, n + 1):
sum += int(n / i) * i
return int(sum)
n = 4
print( divisorSum(n))
n = 5
print( divisorSum(n))
|
C#
using System;
class GFG {
static int divisorSum(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
sum += (n / i) * i;
return sum;
}
public static void Main()
{
int n = 4;
Console.WriteLine(divisorSum(n));
n = 5;
Console.WriteLine(divisorSum(n));
}
}
|
Javascript
function divisorSum(n)
{
let sum = 0;
for (let i = 1; i <= n; ++i)
sum += Math.floor(n / i) * i;
return sum;
}
let n = 4;
document.write(divisorSum(n) + "<br>");
n = 5;
document.write(divisorSum(n) + "<br>");
|
PHP
<?php
function divisorSum( $n)
{
$sum = 0;
for ( $i = 1; $i <= $n; ++$i)
$sum += floor($n / $i) * $i;
return $sum;
}
$n = 4;
echo divisorSum($n),"\n";
$n = 5;
echo divisorSum($n),"\n";
?>
|
Time complexity: O(n)
Auxiliary space: O(1)
More efficient solution:
We need to calculate
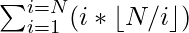
To evaluate the above expression in O(sqrt(N)) we make use of The Harmonic Lemma.
Consider the harmonic sequence on integer division: {N/1, N/2, N/3, ….. ,N/N}
The lemma states that the above sequence is non-increasing, and there are at most 2*sqrt(N) different elements.
Consider floor(N/i) = k. Thus, k <= N/i < k+1. From this we get largest = floor(N/k). Therefore, we can find a range of values of i for which floor(N/i) is constant. And using The Harmonic Lemma we know that will be at most 2*sqrt(N) terms, thus we can calculate it programmatically in O(sqrt(N)) complexity. Consider the following example for better clarification.
C++
#include <iostream>
using namespace std;
#define ll long long
#define mod 1000000007
ll power(ll x, ll y, ll p)
{
ll res = 1;
x = x % p;
while (y > 0)
{
if (y & 1)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return (res + p) % p;
}
ll modinv(ll x)
{
return power(x, mod - 2, mod);
}
ll sum(ll n)
{
ll retval = ((((n % mod) * ((n + 1) %
mod)) % mod) * modinv(2)) % mod;
return retval;
}
ll divisorSum(ll n)
{
ll l = 1;
ll ans = 0;
while (l <= n)
{
ll k = n / l;
ll r = n / k;
k %= mod;
ans += ((sum(r) - sum(l - 1) %
mod) * k) % mod;
ans %= mod;
l = r + 1;
}
ans = ans % mod;
if (ans < 0){
return ans+mod;
}else{
return ans;
}
}
int main()
{
int n = 5;
cout << "The sum of divisors of all numbers from 1 to " << n << " is: " \
<< divisorSum(n) << '\n';
n = 14;
cout << "The sum of divisors of all numbers from 1 to " << n << " is: " \
<< divisorSum(n) << '\n';
}
|
Java
import java.util.*;
class Main{
static int mod = 1000000007;
public static long power(long x,
long y,
long p)
{
long res = 1;
x = x % p;
while (y > 0)
{
if ((y & 1) != 0)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return (res + p) % p;
}
public static long modinv(long x)
{
return power(x, mod - 2, mod);
}
public static long sum(long n)
{
long retval = ((((n % mod) * ((n + 1) %
mod)) % mod) * modinv(2)) %
mod;
return retval;
}
public static long divisorSum(long n)
{
long l = 1;
long ans = 0;
while (l <= n)
{
long k = n / l;
long r = n / k;
k %= mod;
ans += ((sum(r) - sum(l - 1) %
mod) * k) % mod;
ans %= mod;
l = r + 1;
}
ans = ans % mod;
return ans;
}
public static void main(String[] args)
{
int n = 5;
System.out.println("The sum of divisors of" +
" all numbers from 1 to " +
n + " is: " + divisorSum(n));
n = 14;
System.out.println("The sum of divisors of all" +
" numbers from 1 to " + n +
" is: " + divisorSum(n));
}
}
|
Python3
mod = 1000000007;
def power(x, y, p):
res = 1;
x = x % p;
while (y > 0):
if ((y & 1) != 0):
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
return (res + p) % p;
def modinv(x):
return power(x, mod - 2, mod);
def sum(n):
retval = ((((n % mod) * ((n + 1) % mod)) % mod) * modinv(2)) % mod;
return retval;
def divisorSum(n):
l = 1;
ans = 0;
while (l <= n):
k = n // l;
r = n // k;
k %= mod;
ans += ((sum(r) - sum(l - 1) % mod) * k) % mod;
ans %= mod;
l = r + 1;
ans = ans % mod;
return ans;
if __name__ == '__main__':
n = 5;
print("The sum of divisors of all numbers from 1 to " , n , " is: " ,int( divisorSum(n)));
n = 14;
print("The sum of divisors of all numbers from 1 to ", n ," is: " , int(divisorSum(n)));
|
C#
using System;
class GFG{
static int mod = 1000000007;
static long power(long x, long y, long p)
{
long res = 1;
x = x % p;
while (y > 0)
{
if ((y & 1) != 0)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return (res + p) % p;
}
static long modinv(long x)
{
return power(x, mod - 2, mod);
}
static long sum(long n)
{
long retval = ((((n % mod) * ((n + 1) %
mod)) % mod) * modinv(2)) %
mod;
return retval;
}
static long divisorSum(long n)
{
long l = 1;
long ans = 0;
while (l <= n)
{
long k = n / l;
long r = n / k;
k %= mod;
ans += ((sum(r) - sum(l - 1) %
mod) * k) % mod;
ans %= mod;
l = r + 1;
}
ans = ans % mod;
return ans;
}
static void Main()
{
int n = 5;
Console.WriteLine("The sum of divisors of" +
" all numbers from 1 to " +
n + " is: " + divisorSum(n));
n = 14;
Console.WriteLine("The sum of divisors of all" +
" numbers from 1 to " + n +
" is: " + divisorSum(n));
}
}
|
Javascript
<script>
var mod = 10007;
function power(x, y, p)
{
var res = 1;
x = x % p;
while (y > 0)
{
if ((y & 1) != 0)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return (res + p) % p;
}
function modinv(x)
{
return power(x, mod - 2, mod);
}
function sum(n)
{
var retval = Math.floor((((n % mod) * ((n + 1) %
mod)) % mod) * modinv(2)) %
mod;
return retval;
}
function divisorSum(n)
{
var l = 1;
var ans = 0;
while (l <= n)
{
var k = n / l;
var r = n / k;
k %= mod;
ans += Math.floor((sum(r) - sum(l - 1) %
mod) * k) % mod;
ans %= mod;
l = r + 1;
}
ans = ans % mod;
return ans;
}
var n = 5;
document.write("The sum of divisors of" +
" all numbers from 1 to " +
n + " is: " + divisorSum(n) +"<br>");
n = 14;
document.write("The sum of divisors of all" +
" numbers from 1 to " + n +
" is: " + divisorSum(n));
</script>
|
OutputThe sum of divisors of all numbers from 1 to 5 is: 21
The sum of divisors of all numbers from 1 to 14 is: 165
Time complexity: O(sqrt(N))
Auxiliary space: O(1)
Another sqrt(n) approach:
Anywhere division is used in the below article, it means integer division.
Let’s start with an example assume that n = 20, now let’s see how each number from 1 to 20 appears as the factor of some other number.
1 : 1 * 1, 1 * 2, 1 * 3, 1 * 4..., 1 * (20 / 1)
2 : 2 * 1, 2 * 2, 2 * 3, 2 * 4,..., 2 * (20 / 2)
3 : 3 * 1, 3 * 2, 3 * 3, 3 * 4...., 3 * (20 / 3)
our goal is to add every number each time it appears as the factor of some other number. For example 3 appears as the factor of (3 * 1), (3 * 2), (3 * 3)…, (3 * (20 / 3)). Now let’s start from 1 and add 1 to our sum each time it appears and also we will add all the numbers that appeared with 1, we’ll do the same thing with 2 and when we reach 3 we have already added 3 to our sum when it appeared with 1 and 2 so now we will only add 3 when it appears with numbers greater than 2 i.e. 3, 4, 5, 6 also we will add the numbers that appeared with 3 so we’ll add 4, 5 and 6 as well (notice here we will not add 3 twice because of 3 * 3). Similarly when we reach 4 we have already added 4 when it appeared with 1, 2 and 3 so we’ll add it only when it appears with numbers >= itself and add the numbers that appear with 4.
Finally we can say that when we are at a number i, we have already processed numbers from1 to i – 1 and hence we have added i every time it appears with numbers 1 to i – 1 so this time we only need to add i every time it appears with numbers >= i also we have to add all the numbers that appear together with i and they are > i.
Therefore for every number i we want to add the following terms to our sum
t1 : (add i each time it appears with numbers >= itself) -> i * (num / i - (i - 1))
(recall i will appear with numbers 1 to num / i
and we have already added i each time it appeared with a numbers less than itself)
t2 : (add numbers that appear with i) -> (i + 1) + (i + 2) ... + (num / i)
(numbers 1 to num / i will appear with i but
we have already processed numbers 1 to i - 1 and added them
when they appeared with i so now we only have to add the numbers
that appear with i and are greater than i,
here we will not add i itself because when i appears with itself
it should be added only once and we have added it once in t1)
we need to calculate t2 in O(1) time, here's how to do that
t2 = (i + 1) + (i + 2) + (i + 3) + ... + (num / i)
add and subtract 1 + 2 + 3 ... + i
=> t2 = 1 + 2 + 3 + ... + i + (i + 1) + (i + 2) + ... + (num / i) - (1 + 2 + 3 + ... + i)
=> t2 = (1 + 2 + 3 + .. + (num / i)) - (1 + 2 + 3 .. + i)
=> t2 = ((num / i) * (num / i + 1)) / 2 - (i * (i + 1)) / 2
Finally, let’s look at the numbers that are greater than sqrt(num). These numbers will only appear with numbers that are lesser than sqrt(num). Let’s say x is a number greater than sqrt(num)
we have,
x > sqrt(num)
multiply sqrt(num) on both sides
=> x * sqrt(num) > sqrt(num) * sqrt(num)
=> x * sqrt(num) > num
we want to add x each time it appears, from above proof we see that x multiplied by root of num itself is greater than num hence x will only appear with numbers less than root of num so if we process all the numbers from 1 to sqrt(num) we will add every time x appears. For example take n = 100 now consider 11, 11 * 10 > 100 so 11 appears only with 1 to 9 i.e. as a factor of 11, 22, 33,…, 99 same is true for rest of the numbers that are greater than 10 they will only appear with numbers lesser than 10 and hence we only need to process numbers from 1 to 10 to add the numbers greater than 10 for n = 100.
Finally, our solution is this
for each i in 1 to sqrt(num) //no need to visit numbers greater than the root
add t1 and t2 to the sum
below is the c++ code
C++
#include <bits/stdc++.h>
using namespace std;
long long sum_all_divisors(long long num)
{
long long sum = 0;
for (long long i = 1; i <= sqrt(num); i++) {
long long t1 = i * (num / i - i + 1);
long long t2 = (((num / i) * (num / i + 1)) / 2) - ((i * (i + 1)) / 2);
sum += t1 + t2;
}
return sum;
}
int main()
{
int n;
long long sum = sum_all_divisors(n);
cout << sum << '\n';
return 0;
}
|
Java
import java.io.*;
class GFG {
public static int sum_all_divisors(int num)
{
int sum = 0;
for (int i = 1; i <= Math.sqrt(num); i++) {
int t1 = i * (num / i - i + 1);
int t2 = (((num / i) * (num / i + 1)) / 2) - ((i * (i + 1)) / 2);
sum += t1 + t2;
}
return sum;
}
public static void main (String[] args)
{
int n = 1;
int sum = sum_all_divisors(n);
System.out.println(sum);
}
}
|
Python3
import math
def sum_all_divisors(num):
sum = 0;
for i in range(1,math.floor(math.sqrt(num))+1):
t1 = i * (num / i - i + 1)
t2 = (((num / i) * (num / i + 1)) / 2) - ((i * (i + 1)) / 2)
sum += t1 + t2;
return sum;
n = 1
sum = sum_all_divisors(n)
print(sum)
|
C#
using System;
class GFG {
public static int sum_all_divisors(int num)
{
int sum = 0;
for (int i = 1; i <= Math.Sqrt(num); i++) {
int t1 = i * (num / i - i + 1);
int t2 = (((num / i) * (num / i + 1)) / 2) - ((i * (i + 1)) / 2);
sum += t1 + t2;
}
return sum;
}
public static void Main (String[] args)
{
int n = 1;
int sum = sum_all_divisors(n);
Console.Write(sum);
}
}
|
Javascript
<script>
function sum_all_divisors(num)
{
var sum = 0;
for (var i = 1; i <= Math.sqrt(num); i++) {
var t1 = i * (num / i - i + 1);
var t2 = (((num / i) * (num / i + 1)) / 2) - ((i * (i + 1)) / 2);
sum += t1 + t2;
}
return sum;
}
var n;
var sum = sum_all_divisors(n);
document.write( sum );
</script>
|
Time complexity: O(sqrt(N))
Auxiliary space: O(1)
Example in c:
Approach:
1. Create an array divisor_sum of size n+1, initialized with 1 for each index.
2. Loop through each prime p (starting from 2) and check if divisor_sum[p] is equal to 1. If so, update divisor_sum for each multiple of p using the formula: divisor_sum[i] *= (1 – pow(p, exp+1)) / (1 – p), where exp is the highest power of p that divides i.
3. For each prime p, add divisor_sum[p] to the variable sum.
4. Return sum.
C++
#include <bits/stdc++.h>
using namespace std;
int sum_of_divisors(int n) {
int sum = 1;
int divisor_sum[n+1];
for (int i = 1; i <= n; i++) {
divisor_sum[i] = 1;
}
for (int p = 2; p <= n; p++) {
if (divisor_sum[p] == 1) {
for (int i = p; i <= n; i += p) {
int exp = 0;
int q = i;
while (q % p == 0) {
exp++;
q /= p;
}
divisor_sum[i] *= (1 - pow(p, exp+1)) / (1 - p);
}
}
sum += divisor_sum[p];
}
return sum;
}
int main() {
int n = 4;
int sum = sum_of_divisors(n);
cout<<"The sum of all divisors from 1 to "<<n<<" is "<<sum<<endl;
return 0;
}
|
C
#include <stdio.h>
#include <math.h>
int power(int p,int exp)
{
int res=1;
for(int i=0;i<exp;i++)
{
res=res*p;
}
return res;
}
int sum_of_divisors(int n) {
int sum = 1;
int divisor_sum[n+1];
for (int i = 1; i <= n; i++) {
divisor_sum[i] = 1;
}
for (int p = 2; p <= n; p++) {
if (divisor_sum[p] == 1) {
for (int i = p; i <= n; i += p) {
int exp = 0;
int q = i;
while (q % p == 0) {
exp++;
q /= p;
}
divisor_sum[i] *= (1 - power(p, exp+1)) / (1 - p);
}
}
sum += divisor_sum[p];
}
return sum;
}
int main() {
int n = 4;
int sum = sum_of_divisors(n);
printf("The sum of all divisors from 1 to %d is %d\n", n, sum);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int sum_of_divisors(int n) {
int sum = 1;
int divisor_sum[] = new int[n+1];
for (int i = 1; i <= n; i++) {
divisor_sum[i] = 1;
}
for (int p = 2; p <= n; p++) {
if (divisor_sum[p] == 1) {
for (int i = p; i <= n; i += p) {
int exp = 0;
int q = i;
while (q % p == 0) {
exp++;
q /= p;
}
int temp = (int)Math.pow(p,exp+1);
divisor_sum[i]*= (1 - temp) / (1 - p);
}
}
sum += divisor_sum[p];
}
return sum;
}
public static void main (String[] args) {
int n = 4;
int sum = sum_of_divisors(n);
System.out.println("The sum of all divisors from 1 to "+n+" is "+sum);
}
}
|
Python3
import math
def sum_of_divisors(n):
sum = 1
divisor_sum = [1] * (n+1)
for i in range(2, n+1):
if divisor_sum[i] == 1:
for j in range(i, n+1, i):
exp = 0
q = j
while q % i == 0:
exp += 1
q //= i
divisor_sum[j] *= (1 - math.pow(i,exp+1)) // (1 - i)
sum += divisor_sum[i]
return sum
n = 4
sum = sum_of_divisors(n)
print(f"The sum of all divisors from 1 to {n} is {sum}")
|
C#
using System;
class Program {
static int sum_of_divisors(int n) {
int sum = 1;
int[] divisor_sum = new int[n+1];
for (int i = 1; i <= n; i++) {
divisor_sum[i] = 1;
}
for (int p = 2; p <= n; p++) {
if (divisor_sum[p] == 1) {
for (int i = p; i <= n; i += p) {
int exp = 0;
int q = i;
while (q % p == 0) {
exp++;
q /= p;
}
divisor_sum[i] *= (1 - (int)Math.Pow(p, exp+1)) / (1 - p);
}
}
sum += divisor_sum[p];
}
return sum;
}
static void Main(string[] args) {
int n = 4;
int sum = sum_of_divisors(n);
Console.WriteLine("The sum of all divisors from 1 to " + n + " is " + sum);
}
}
|
Javascript
function sum_of_divisors(n) {
let sum = 1;
let divisor_sum = new Array(n + 1).fill(1);
for (let p = 2; p <= n; p++) {
if (divisor_sum[p] === 1) {
for (let i = p; i <= n; i += p) {
let exp = 0;
let q = i;
while (q % p === 0) {
exp++;
q /= p;
}
let temp = Math.pow(p, exp + 1);
divisor_sum[i] *= (1 - temp) / (1 - p);
}
}
sum += divisor_sum[p];
}
return sum;
}
let n = 4;
let sum = sum_of_divisors(n);
console.log(`The sum of all divisors from 1 to ${n} is ${sum}`);
|
OutputThe sum of all divisors from 1 to 4 is 15
The time complexity of this approach is O(n log log n) .
The space complexity is O(n) for the divisor_sum array.
Approach:
1. We initialize n to the maximum number till which we want to find the sum of divisors. In this example, we have taken n as 10.
2. We initialize an array of size n+1 to store the sum of divisors for each number from 1 to n.
3. We use two nested loops to iterate through all the numbers from 1 to n. The outer loop runs from 1 to n, while the inner loop runs from i to n in steps of i.
4. For each number j that is a multiple of i, we add i to the sum of divisors for j. This is done by accessing the array element divisors[j] and incrementing it by i.
5. Finally, we iterate through the array of sum of divisors and add up all the values to get the total sum of divisors from 1 to n.
C++
#include <bits/stdc++.h>
using namespace std;
#define MAXN 1000000
int main()
{
int n = 10;
int i, j;
int sum = 0;
int divisors[MAXN+1] = {0};
for (i = 1; i <= n; i++) {
for (j = i; j <= n; j += i) {
divisors[j] += i;
}
}
for (i = 1; i <= n; i++) {
sum += divisors[i];
}
cout<<"The sum of all divisors from 1 to "<<n<<" is "<<sum<<endl;
return 0;
}
|
C
#include <stdio.h>
#define MAXN 1000000
int main()
{
int n = 10;
int i, j;
int sum = 0;
int divisors[MAXN+1] = {0};
for (i = 1; i <= n; i++) {
for (j = i; j <= n; j += i) {
divisors[j] += i;
}
}
for (i = 1; i <= n; i++) {
sum += divisors[i];
}
printf("The sum of all divisors from 1 to %d is %d\n", n, sum);
return 0;
}
|
Java
import java.util.*;
public class Main {
public static void main(String[] args) {
int n = 10;
int i, j;
int sum = 0;
int[] divisors = new int[1000001];
for (i = 1; i <= n; i++) {
for (j = i; j <= n; j += i) {
divisors[j] += i;
}
}
for (i = 1; i <= n; i++) {
sum += divisors[i];
}
System.out.println("The sum of all divisors from 1 to " + n + " is " + sum);
}
}
|
Python3
MAXN = 1000000
n = 10
sum = 0
divisors = [0] * (MAXN+1)
for i in range(1, n+1):
for j in range(i, n+1, i):
divisors[j] += i
for i in range(1, n+1):
sum += divisors[i]
print(f"The sum of all divisors from 1 to {n} is {sum}")
|
C#
using System;
class Program
{
const int MAXN = 1000000;
static void Main(string[] args)
{
int n = 10;
int i, j;
int sum = 0;
int[] divisors = new int[MAXN+1];
for (i = 1; i <= n; i++) {
for (j = i; j <= n; j += i) {
divisors[j] += i;
}
}
for (i = 1; i <= n; i++) {
sum += divisors[i];
}
Console.WriteLine("The sum of all divisors from 1 to {0} is {1}", n, sum);
}
}
|
Javascript
function main() {
const n = 10;
let i, j;
let sum = 0;
const divisors = new Array(1000001).fill(0);
for (i = 1; i <= n; i++) {
for (j = i; j <= n; j += i) {
divisors[j] += i;
}
}
for (i = 1; i <= n; i++) {
sum += divisors[i];
}
console.log("The sum of all divisors from 1 to " + n + " is " + sum);
}
main();
|
OutputThe sum of all divisors from 1 to 10 is 87
Time Complexity: O(nloglogn), where n is the maximum number till which we want to find the sum of divisors.
Space Complexity: O(n), as we are using an array of size n to store the sum of divisors.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...