Sum of dependencies in a graph
Last Updated :
13 Sep, 2023
Given a directed and connected graph with n nodes. If there is an edge from u to v then u depends on v. Our task was to find out the sum of dependencies for every node.
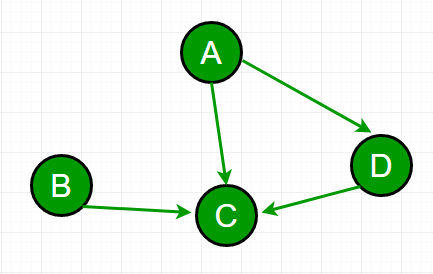
Example:
For the graph in diagram,
A depends on C and D i.e. 2
B depends on C i.e. 1
D depends on C i.e. 1
And C depends on none.
Hence answer -> 0 + 1 + 1 + 2 = 4
Asked in : Flipkart Interview
Idea is to check adjacency list and find how many edges are there from each vertex and return the total number of edges.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
void addEdge(vector <int> adj[], int u,int v)
{
adj[u].push_back(v);
}
int findSum(vector<int> adj[], int V)
{
int sum = 0;
for (int u = 0; u < V; u++)
sum += adj[u].size();
return sum;
}
int main()
{
int V = 4;
vector<int >adj[V];
addEdge(adj, 0, 2);
addEdge(adj, 0, 3);
addEdge(adj, 1, 3);
addEdge(adj, 2, 3);
cout << "Sum of dependencies is "
<< findSum(adj, V);
return 0;
}
|
Java
import java.util.Vector;
class Test
{
static void addEdge(Vector <Integer> adj[], int u,int v)
{
adj[u].addElement((v));
}
static int findSum(Vector<Integer> adj[], int V)
{
int sum = 0;
for (int u = 0; u < V; u++)
sum += adj[u].size();
return sum;
}
public static void main(String[] args)
{
int V = 4;
@SuppressWarnings("unchecked")
Vector<Integer> adj[] = new Vector[V];
for (int i = 0; i < adj.length; i++) {
adj[i] = new Vector<>();
}
addEdge(adj, 0, 2);
addEdge(adj, 0, 3);
addEdge(adj, 1, 3);
addEdge(adj, 2, 3);
System.out.println("Sum of dependencies is " +
findSum(adj, V));
}
}
|
Python3
def addEdge(adj, u, v):
adj[u].append(v)
def findSum(adj, V):
sum = 0
for u in range(V):
sum += len(adj[u])
return sum
if __name__=='__main__':
V = 4
adj = [[] for i in range(V)]
addEdge(adj, 0, 2)
addEdge(adj, 0, 3)
addEdge(adj, 1, 3)
addEdge(adj, 2, 3)
print("Sum of dependencies is",
findSum(adj, V))
|
C#
using System;
using System.Collections;
class GFG{
static void addEdge(ArrayList []adj, int u,
int v)
{
adj[u].Add(v);
}
static int findSum(ArrayList []adj, int V)
{
int sum = 0;
for(int u = 0; u < V; u++)
sum += adj[u].Count;
return sum;
}
public static void Main(string[] args)
{
int V = 4;
ArrayList []adj = new ArrayList[V];
for(int i = 0; i < V; i++)
{
adj[i] = new ArrayList();
}
addEdge(adj, 0, 2);
addEdge(adj, 0, 3);
addEdge(adj, 1, 3);
addEdge(adj, 2, 3);
Console.Write("Sum of dependencies is " +
findSum(adj, V));
}
}
|
Javascript
let V = 4;
let adj = new Array(V).fill(null).map(() => []);
addEdge(adj, 0, 2);
addEdge(adj, 0, 3);
addEdge(adj, 1, 3);
addEdge(adj, 2, 3);
console.log(`Sum of dependencies is ${findSum(adj, V)}`);
function addEdge(adj, u, v) {
adj[u].push(v);
}
function findSum(adj, V) {
let sum = 0;
for (let u = 0; u < V; u++) {
sum += adj[u].length;
}
return sum;
}
|
Output
Sum of dependencies is 4
Time complexity: O(V) where V is number of vertices in graph.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...