Subtracting Fractions

To subtract fractions, first check and find the common denominator, then subtract the numerators and simply the resultant fraction if possible. Subtracting fractions involves making the denominators (bottom number) same by finding the lowest common multiple of them and subtracting the numerators (top number) and finally simplifying the fraction if possible.

In this article, we will learn about, subtracting fractions, examples, and others in detail.

How to Subtract Fractions?

Here are the steps for subtracting fractions:

1. Identify the denominators: Check if the fractions have the same denominators. Fractions with the same denominators are called like fractions.
2. Find the common denominator: If the fractions have different denominators, find the smallest common denominator. This can be done by identifying the least common multiple of the two denominators.
3. Subtract the numerators: Subtract the top numbers (the numerators). Put the answer over the same denominator.
4. Simplify: Simplify the fraction if needed.

Here’s an example of subtracting fractions with the same denominator:

5/7 – 2/7 = (5 – 2)/7 = 3/7

Fractions can be like fractions and unlike fractions and they can be easily subtracted using the steps explained ahead.

Subtracting Fractions with Unlike Denominators

When subtracting dissimilar fractions with unlike denominators we need to use the following steps:

Step 1: Identify the unlike denominators of the fractions you want to subtract.

Step 2: Find least common multiple (LCM) of the denominators i.e., the smallest number that is divisible by all denominators.

Step 3: Multiply numerator and denominator by the factor of LCM to make denominators equal.

Step 4: Subtract the numerators of the fractions, keeping the LCM as the denominator. 

Step 5: Simplify the result, if possible.

Example of Subtracting Fractions with Unlike Denominators

Let’s consider some solved examples of subtraction of dissimilar fractions with different denominators to understand the concept and method better.

Example: Subtract 3/5 from 1/3

Step 1: Identify unlike denominators of the fractions you want to subtract.

Denominators are 5 and 3, which are unlike.

Step 2: Find least common multiple (LCM) of the denominators.

Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, …

Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, …

LCM of 5 and 3 is 15

Step 3: Multiply numerator and denominator by the factor of LCM to make denominators equal.

• 1/3 = (1 × 5)/(3 × 5) = 5/15
• 3/5 = (3 × 3)/(5 × 3) = 9/15

Step 4: Subtract the numerators of the fractions, keeping the LCM as the denominator.

9/15 – 5/15 = 4/15

Step 5: Simplify the result, if possible.

4/15 cannot be simplified any further, so the final answer is 4/15.

Let’s consider one more example for better understanding.

Example: Consider two numbers 1/3 and 4/5. Subtract a smaller fraction from the larger one.

Given two fractions: 1/3 and 4/5

To perform Subtraction or even to compare the two numbers, we will need to have a common denominator for both of them

Given First Fractional Number: 1/3

Given Second Fractional Number: 4/5

Numbers in Denominator: 3 for the first number and 5 for the second number.

We will find LCM of the numbers 3 and 5

LCM of 3 and 5 is 15.

So, to attain 15 as denominator, the multiplying factor for numerator and denominator for first fractional number is 5 and for second fractional number is 3

First Fractional Number: (1×5)/(3×5) = 5/15

Second Fractional Number: (4×3)/(5×3) = 12/15

Since denominator is same, we will compare numerators. Clearly, 12/15 is greater than 5/15. So, we will subtract 5/15 from 12/15

Second Fractional Number > First Fractional Number

Second Fractional Number – First Fractional Number

= (12/15) – (5/15)

= (12 – 5)/15

= 7/15

Let’s consider an example of 2/3 – 1/4 for this illustration.

To subtract the 1/4 from 2/3, we take the LCM of the denominators which can be represented by partitioning the circle into equal parts as follows:

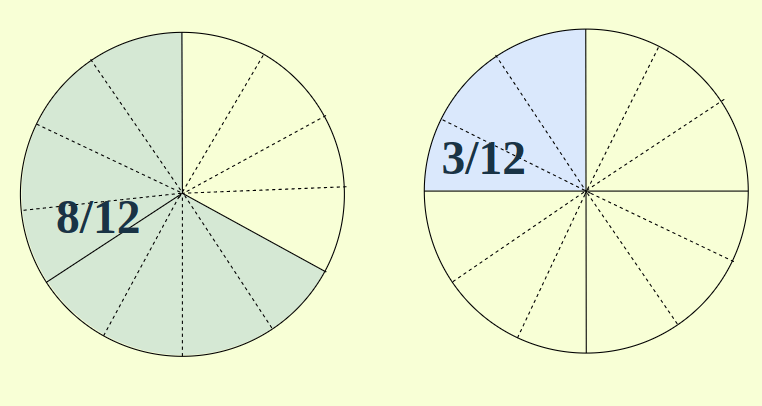
Now, each partition of both circles represents an equal area, thus we can subtract them as a single unit.

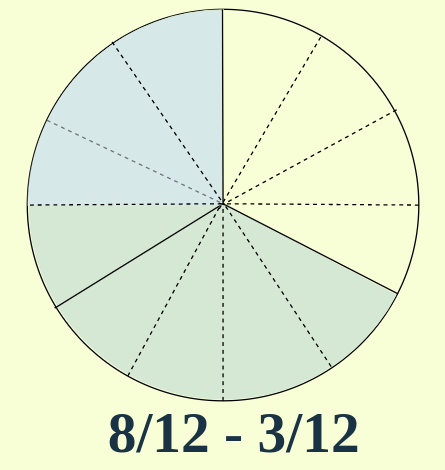
Therefore, 8/12 – 3/12 = 5/12 i.e., 5 parts out of 12 equal parts.

Subtracting Fractions with Like Denominators

Subtracting fractions with like denominators is comparatively easy as in this you don’t need to equalize the denominator by taking LCM and multiplying the required factor in the denominator. One should follow the below-mentioned steps for subtracting fractions with like denominators.

Step 1: First identify larger and smaller fractions. If two fractions have the same denominators then the fraction with a larger denominator is larger.

Step 2: Arrange the fraction for subtraction and take the LCM of the denominator. The LCM of the same number is the number itself.

Step 3: Since, the LCM is same the factor on dividing LCM and the denominator is 1 with which multiply the numerators.

Step 4: Subtract the numerators mentioned in the fraction and write the same denominator to get the answer.

Example: Find the difference between 5/4 and 3/4

Step 1: Since the denominator is the same therefore fraction with a larger denominator is larger. Hence, 5/4 > 3/4.

Step 2: Arrange the fraction 5/4 – 3/4. Now the LCM of 4 will be 4.

Step 3: On dividing LCM 4 by denominator 4 we get 1 which we will multiply with numerators 5 and 3.

Step 4: Hence, on multiplying with 1 we get (5-3)/4 as the fraction. Thus 2/4 is our desired result.

Note: If the fraction can be reduced to simpler forms, reduce it. For example, here we can reduce 2/4 to 1/2.

Subtracting Fractions With Like Denominators Example

In this section, we will understand subtracting fractions having the same denominators with the help of the pictures. For Example, let us assume we have to subtract 3/4 and 1/4

The image added below shows 3/4 of a whole and 1/4 of a whole.

When the denominators are the same, there’s no need to find the Least Common Multiple (LCM). The image won’t be divided further, like we did in the case of different denominators.

Now the only thing we have to do is to subtract the numerators while keeping the denominators the same to get the desired result. Also, check if the obtained result can be further reduced to simpler forms to get the final result. Hence, our result will be (3 – 1)/4 = 2/4 = 1/2 which is shown in the figure below.

Also, learn about Addition of Fractions

Subtracting Fractions With Whole Numbers

As we have subtract two fractions in the same way we can easily subtract a fraction with whole numbers or vice-versa. Mathematically whole number is noting but a fraction with denominator 1 and subtracting them is easily don using steps added above in the article.

For example, Subtract 7 from 19/2

= 19/2 – 7

= 19/2 – 7/1

= 19/2 – 14/2

= (19 – 14)/2

= 5/2

Common Mistakes While Subtracting Fractions

Some common mistakes while subtracting fractions are as follows:

• Error in Finding LCM of Denominators: Calculating LCM for two or more numbers seems easy but sometimes you can find errors in the calculation when there are more than two numbers. So, calculate LCM carefully. Also, calculate LCM very first as either you need to add or subtract fractions with unlike denominators requires the denominators to be the same. 
• Not Simplifying Answer: Most textbooks follow the answer in the standard form and the standard form for the fractional answer is always simplified. Thus always simplify your answer at last.
• Simplifying too Soon: When subtracting fractions, it is important to simplify the resulting fraction only after you have subtracted the numerators and found a common denominator. Simplifying too soon can lead to inconvenience and incorrect answers.

Sample Problems on Subtracting Fractions

Various problems on subtracting fractions are,

Problem 1: Subtract 1/3 from 1/2.

Solution:

Find LCM of numbers 3 & 2

LCM of 3 & 2 is 6

So, to attain 6 as denominator, the multiplying factor for numerator and denominator for first fractional number is 2 and for second fractional number is 3

First Fractional Number: (1×2)/(3×2) = 2/6

Second Fractional Number: (1×3)/(2×3) = 3/6

= (1×3)/(2×3) – (1×2/3×2)

= (3/6) – (2/6)

= 1/6

Problem 2: Subtract 1/4 from 1/3.

Solution:

Find LCM of the numbers 4 & 3

LCM of 4 & 3 is 12

So, to attain 12 as denominator, the multiplying factor for numerator and denominator for first fractional number is 3 and for second fractional number is 4

First Fractional Number: (1×3)/(4×3) = 3/12

Second Fractional Number: (1×4)/(3×4) = 4/12

= [(1×4)/(3×4) – (1×3)/(4×3)]

= (4/12) – (3/12) 

= 1/12

Problem 3: Subtract 1/4 from 1/2.

Solution:

Find LCM of the numbers 4 & 2

LCM of 4 & 2 is 4.

So, to attain 4 as denominator, the multiplying factor for numerator and denominator for first fractional number is 1 and for second fractional number is 2

First Fractional Number: (1×1)/(4×1) = 1/4

Second Fractional Number: (1×2)/(2×2) = 2/4

= [(1×2)/(2×2) – (1×1)/(4×1)]

= (2/4) – (1/4)

= 1/4

Problem 4: Subtract 1/5 from 1/2.

Solution:

Find LCM of the numbers 5 & 2

LCM of 5 & 2 is 10

So, to attain 10 as denominator, the multiplying factor for numerator and denominator for first fractional number is 2 and for second fractional number is 5

First Fractional Number: (1×2)/(5×2) = 2/10

Second Fractional Number: (1×5)/(2×5) = 5/10

= (5/10) – (2/10)

= 3/10

FAQs on Subtract Fractions

1. What are Fractions with Unlike Denominators?

Fractions with unlike denominators are fractions that have different numbers in their denominators. For example, 1/3 and 1/4 are fractions with unlike denominators.

2. What is Subtracting Fractions with Unlike Denominators?

Subtracting fractions with unlike denominators is the process of finding the difference between two fractions that have different numbers in their denominators.

3. How do Subtract Fractions with Different Denominators?

To subtract fractions with unlike denominators, you need to find a common denominator for the fractions, then convert each fraction to an equivalent fraction with the common denominator. Once the fractions have the same denominator, you can subtract the numerators and simplify the result if possible.

4. What is the Common Denominator?

The common denominator is the least common multiple of the denominators of two or more fractions. It is the smallest number that both denominators can divide into evenly.

5. What are Some Tips for Subtracting Fractions with Unlike Denominators?

Here are few tips for subtracting fractions with unlike denominators:

• Always find the common denominator first.
• Keep track of the sign (positive or negative) of each fraction when subtracting.
• Simplify the result if possible.
• Double-check your answer by verifying that it is in the lowest terms and cannot be simplified further.