Subset Equality is NP Complete
Last Updated :
02 Nov, 2023
Subset Equality Problem: Given a set S of non-negative integer values, the problem is to identify if there is a partition of the set S into two sets X and Y, such that, the integer sum in X is equal to the sum of integers in Y.
Explanation:
An instance of the problem is an input specified to the problem. An instance of the Subset Equality Problem is a set S. Since an NP-Complete problem is a problem which is both in NP and NP-hard, the proof for the statement that a problem is NP-Complete consists of two parts:
- The problem itself is in NP class.
- All other problems in NP class can be polynomial-time reducible to that.(B is polynomial-time reducible to C is denoted as B ≤ PC)
If the 2nd condition is only satisfied then the problem is called NP-Hard.
But it is not possible to reduce every NP problem into another NP problem to show its NP-Completeness all the time. Therefore, to show a problem is NP-Complete, then proof that the problem is in NP and any NP-Complete problem is reducible to that i.e., if B is NP-Complete and B ≤ PC then for C in NP, then C is NP-Complete. Thus, it can be concluded that the Subset Equality Problem is NP-Complete using the following two propositions:
- Subset equality is in NP
- Subset equality is NP-Hard
This two proposition can be proved as the Subset Equality Problem is a special case of the Subset Sum Problem where the sum of each partition of subset X and Y in S can be set as: 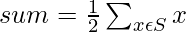
Since the subset-sum is NP-Complete, the subset equality problem also becomes NP-Complete.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...