Subarray with no pair sum divisible by K
Last Updated :
01 Feb, 2023
Given an array of N non-negative integers, task is to find the maximum size of a subarray such that the pairwise sum of the elements of this subarray is not divisible by a given integer, K. Also, print this subarray as well. If there are two or more subarrays that follow the above stated condition, then print the first one from the left.
Prerequisite : Subset with no pair sum divisible by K
Examples :
Input : arr[] = [3, 7, 1, 9, 2]
K = 3
Output : 3
[3, 7, 1]
3 + 7 = 10, 3 + 1 = 4, 7 + 1 = 8, all are
not divisible by 3.
It is not possible to get a subarray of size bigger
than 3 with the above-mentioned property.
[7, 1, 9] is also of the same size but [3, 7, 1] comes first.
Input : arr[] = [2, 4, 4, 3]
K = 4
Output : 2
[2, 4]
2 + 4 = 6 is not divisible by 4.
It is not possible to get a subarray of size bigger
than 2 with the above-mentioned property.
[4, 3] is also of the same size but [2, 4] comes first.
Naive Approach: The naive method would be to consider all the subarrays. While considering a subarray, take elements pairwise and compute the sum of the two elements of the pair. If the computed sum is divisible by K, then ignore this subarray and continue with the next subarray. Else, compute the sum of other pairs of this subarray in a similar fashion. If no pair’s sum is a multiple of K, then compare the size of this subarray with the maximum size obtained so far and update if required.
The time complexity of this method would be O(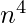 ).
).
Efficient Approach(Using Hashing): We create an empty hash table and insert arr[0] % k into it. Now we traverse remaining elements and maintain a window such that no pair in the window is divisible by k. For every traversed element, we remove starting elements while there exist an element in current window which makes a divisible pair with current element. To check if there is an element in current window, we check if following.
- If there is an element x such that (K – x % K) is equal to arr[i] % K
- OR arr[i] % k is 0 and it exists in the hash.
Once we make sure that all elements which can make a pair with arr[i] are removed, we add arr[i] to current window and check if size of current window is more than the maximum window so far.
Steps to solve this problem:
1. declare a map mp of int key and value.
2. declare variable s=0,e=0,maxs=0,maxe=0.
3. insert mp[arr[0]%k]++.
4. iterate through i=1 till n:
* declare variable mod=arr[i]%k.
* while mp[k-mod] is not equal to zero or mod==0 and mp[mod] is not equal to zero:
* update mp[arr[s]%k]–.
* increment s.
*update mp[mod]++.
*increment e.
*check if ((e-s)>(maxe-maxs)) than update maxe and maxs to e and s.
5. iterating i=maxs till maxe:
* print arr[i].
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
void subarrayDivisibleByK(int arr[], int n, int k)
{
map<int,int> mp;
int s = 0, e = 0, maxs = 0, maxe = 0;
mp[arr[0] % k]++;
for (int i = 1; i < n; i++)
{
int mod = arr[i] % k;
while (mp[k - mod] != 0 ||
(mod == 0 && mp[mod] != 0))
{
mp[arr[s] % k]--;
s++;
}
mp[mod]++;
e++;
if ((e - s) > (maxe - maxs))
{
maxe = e;
maxs = s;
}
}
cout << "The maximum size is "
<< maxe - maxs + 1 << " and "
"the subarray is as follows\n";
for (int i=maxs; i<=maxe; i++)
cout << arr[i] << " ";
}
int main()
{
int k = 3;
int arr[] = {5, 10, 15, 20, 25};
int n = sizeof(arr)/sizeof(arr[0]);
subarrayDivisibleByK(arr, n, k);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
public class GFG {
static void subarrayDivisibleByK(int []arr,
int n, int k)
{
int []mp = new int[1000];
int s = 0, e = 0, maxs = 0, maxe = 0;
mp[arr[0] % k]++;
for (int i = 1; i < n; i++)
{
int mod = arr[i] % k;
while (mp[k - mod] != 0 ||
(mod == 0 && mp[mod] != 0))
{
mp[arr[s] % k]--;
s++;
}
mp[mod]++;
e++;
if ((e - s) > (maxe - maxs))
{
maxe = e;
maxs = s;
}
}
System.out.print("The maximum size is "
+ (maxe - maxs + 1)
+ " and the subarray is as follows\n");
for (int i = maxs; i <= maxe; i++)
System.out.print(arr[i] + " ");
}
public static void main(String args[])
{
int k = 3;
int []arr = {5, 10, 15, 20, 25};
int n = arr.length;
subarrayDivisibleByK(arr, n, k);
}
}
|
Python3
def subarrayDivisibleByK(arr, n, k) :
mp = [0] * 1000
s = 0; e = 0; maxs = 0; maxe = 0;
mp[arr[0] % k] = mp[arr[0] % k] + 1;
for i in range(1, n):
mod = arr[i] % k
while (mp[k - mod] != 0 or (mod == 0
and mp[mod] != 0)) :
mp[arr[s] % k] = mp[arr[s] % k] - 1
s = s + 1
mp[mod] = mp[mod] + 1
e = e + 1
if ((e - s) > (maxe - maxs)) :
maxe = e
maxs = s
print ("The maximum size is {} and the "
" subarray is as follows"
.format((maxe - maxs + 1)))
for i in range(maxs, maxe + 1) :
print ("{} ".format(arr[i]), end="")
k = 3
arr = [5, 10, 15, 20, 25]
n = len(arr)
subarrayDivisibleByK(arr, n, k)
|
C#
using System;
using System.Collections;
class GFG {
static void subarrayDivisibleByK(int []arr,
int n, int k)
{
int []mp = new int[1000];
int s = 0, e = 0, maxs = 0, maxe = 0;
mp[arr[0] % k]++;
for (int i = 1; i < n; i++)
{
int mod = arr[i] % k;
while (mp[k - mod] != 0 ||
(mod == 0 && mp[mod] != 0))
{
mp[arr[s] % k]--;
s++;
}
mp[mod]++;
e++;
if ((e - s) > (maxe - maxs))
{
maxe = e;
maxs = s;
}
}
Console.Write("The maximum size is " +
(maxe - maxs + 1) +
" and the subarray is as follows\n");
for (int i = maxs; i <= maxe; i++)
Console.Write(arr[i] + " ");
}
public static void Main()
{
int k = 3;
int []arr = {5, 10, 15, 20, 25};
int n = arr.Length;
subarrayDivisibleByK(arr, n, k);
}
}
|
PHP
<?php
function subarrayDivisibleByK($arr, $n, $k)
{
$mp = array_fill(0, 1000, 0);
$s = 0;
$e = 0;
$maxs = 0;
$maxe = 0;
$mp[$arr[0] % $k]++;
for ($i = 1; $i < $n; $i++)
{
$mod = $arr[$i] % $k;
while ($mp[$k - $mod] != 0 ||
($mod == 0 &&
$mp[$mod] != 0))
{
$mp[$arr[$s] % $k]--;
$s++;
}
$mp[$mod]++;
$e++;
if (($e - $s) > ($maxe - $maxs))
{
$maxe = $e;
$maxs = $s;
}
}
echo ("The maximum size is ".
($maxe - $maxs + 1).
" and the subarray is".
" as follows\n");
for ($i = $maxs; $i <= $maxe; $i++)
echo ($arr[$i]." ");
}
$k = 3;
$arr = array(5, 10, 15, 20, 25);
$n = count($arr);
subarrayDivisibleByK($arr, $n, $k);
?>
|
Javascript
<script>
function subarrayDivisibleByK(arr, n, k) {
var mp = new Array(1000).fill(0);
var s = 0,
e = 0,
maxs = 0,
maxe = 0;
mp[arr[0] % k]++;
for (var i = 1; i < n; i++) {
var mod = arr[i] % k;
while (mp[k - mod] != 0 || (mod == 0 && mp[mod] != 0)) {
mp[arr[s] % k]--;
s++;
}
mp[mod]++;
e++;
if (e - s > maxe - maxs) {
maxe = e;
maxs = s;
}
}
document.write(
"The maximum size is " +
(maxe - maxs + 1) +
" and the subarray is as follows<br>"
);
for (var i = maxs; i <= maxe; i++) document.write(arr[i] + " ");
}
var k = 3;
var arr = [5, 10, 15, 20, 25];
var n = arr.length;
subarrayDivisibleByK(arr, n, k);
</script>
|
OutputThe maximum size is 2 and the subarray is as follows
10 15
Time Complexity : O(nlogn)
Auxiliary Space: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...