Aspirants who are preparing for the upcoming SSC CGL Exam know the importance of scoring good in the Tier 1 exam. Gone are the days, when the cutoff used to be about 120-130. And, for scoring good in Tier 1 exam, quant plays a very important role. To help you with that, we are here with another solved previous year’s paper for you. This is a solved paper in SSC CGL 2019 Quant Section.
Que 1. The length, breadth and height of a cuboidal box are in the ratio of 7:5:3 and its whole surface area is 27,832 cm². Its volume is –
A) 288120 cm³
B) 265390 cm³
C) 207505 cm³
D) 329000 cm³
Answer A
Explanation
Total surface area of a cuboid = 2(lb+bh+lh)
Here, l = Length ; b= breadth ; h= height
Let, Length= 7P ; Breadth= 5P ; Height=3P
According to question,
2(lb+bh+lh)=27832
=>2(7P×5P+5P×3P+7P×3P)=27832
=>35P²+15P²+21P² = 27832/2
=>71P²=13916
=>P²=13916/71
=>P =√196
=> P=14
:.Volume of the cuboid= lbh =7×14×5×14×3×14
cm³ = 288120 cm³
Que 2. In the given figure a right-angle triangle is shown, what is the value of cosecθ?
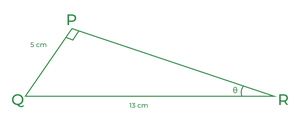
Right Angle Triangle
A) 9/5
B) 13/5
C) 17/5
D) 13/3
Answer B
Explanation
Cosecθ = hypotenuse/perpendicular = 13/5
Important point: Since, QPR is a right-angle triangle, the opposite side of the right angle is called the hypotenuse.
Direction (3-6):
The following table represents the number of candidates that appeared and qualified in a competitive examination from different states over five years. Study the table and answer the questions that follow,
Que 3. The total number of candidates that qualified from all states together in 1998 is approximately what percentage of the total number of candidates that qualified from all the states together in 2001? ( Correct to two decimal points)
A) 97.72%
B) 92.68%
C) 101.85%
D) 88.90 %
Answer A
Explanation
In 1998 total number of qualified candidates in all states
= (980+1050+1020+1240)
= 4290
In 2001 total number of qualified candidates in all states
=(1125+1020+1250+995)
= 4390
:. Required percentage = 4290/4390 ×100%
= 97.72%
Que 4. What was the total number of candidates appearing from all the states in the year 1997?
A) 27,200
B) 29,000
C) 25,300
D) 24,100
Answer A
Explanation
In 1997 total appearing candidates from all the
states= (5200+7500+6400+8100) = 27,200
Que 5. What is the average number of candidates that appeared from state Q during the given year?
A) 8100
B) 8250
C) 8680
D) 8990
Answer D
Explanation
From state Q total number of appeared candidates
= (8100+9500+8700+9700+8950) = 44950
:. Required average = 44950/5 =8990
Que 6. What is the difference between the number of candidates qualifying in the year 1998, in the states M and P?
A) 40
B) 55
C) 60
D) 35
Answer A
Explanation
Required difference=(1020-980) =40
Que 7. Find the value of 1800÷20×{(12-6)+(24-12)}
A) 1530
B) 1620
C) 1390
D) 1800
Answer B
Explanation
1800÷20×{(12-6)+(24-12)}
=1800÷20×(6+12)
=1800÷20×18
=90×18 =1620
Que 8. If 3A=4B=5C, then A: B: C is equal to –
A) 5 : 4 : 3
B) 12 : 15 : 20
C) 9 : 16 : 25
D) 20 : 15 : 12
Answer D
Explanation
3A = 4B = 5C
L.C.M of 3,4,5 = 60
Now,
A : B : C = 60/3 : 60/4 : 60/5
= 20 : 15 : 12
Que 9. Seema flies a kite on a 16 m string at an inclination of 60°. What is the height (h) of the kite above the ground?
A) 8√3 m
B) 16 m
C) 16√3 m
D) 8 m
Answer A
Explanation
sin60° = √3/2 =perpendicular (p)/hypotenuse (h)
Let, Perpendicular = x,
Then, √3/2 = x/ 16
:. Required height =x√3 = 8√3 m
Que 10. What is the smallest integer that is a multiple of 5,8,15?
A) 80
B) 120
C) 100
D) 240
Answer B
Explanation
The smallest number that will be multiple of 5, 8 & 15 is their LCM which is 120.
This is the required smallest integer.
Que 11. The simple Interest on a sum of money for 3 years at an interest of 6% p.a is Rs.6750. What will be the compound interest rounded off on the same sum at the same rate for the same period, compounded annually is closest to
A) 8125
B) 7890
C) 7163
D) 6891
Answer C
Explanation
S.I = (P×R×T)/100
=> 6750=(P×6×3)/100. => P = 37500
Now, 6% = 6/100 = 3/50
For Compound Interest,
Principal Amount
50 53
(50)³ (53)³ ( For 3 years)
125000 148877
Principal =125000/37500 =3.33 times of the actual principal, so the amount should be divided by 3.33 to get the actual amount.
Amount = 148877/3.33 = 44663
Compound Interest=(44663-37500) =7163
Que 12. In the given figure ∆ABC, if θ= 80°, the measure of each of the other two angles will be –
A) 45°
B) 50°
C) 55°
D) 60°
Answer B
Explanation
Here, side AB and AC both are equal. So the two angles related to side AB and AC are also the same.
∠ABC = ∠ACB
We know, the total value of angles of a triangle =180°
∠ABC + ∠ACB +∠BAC(θ) = 180°
=> ∠ABC + ∠ACB = 180° – 80° (∠BAC(θ)= 80°)
:. ∠ABC + ∠ACB = 100°
Now, the value of each angle = 100°/2 = 50°
Tricks:
θ = 80°
If sides are equal then their opposite angles are also equal to each other.
Each of the two angles value = (180°-80°)/2 =50°
Que 13. If 6tanθ – 5√3secθ + 12cotθ = 0, (0°< θ < 90°),then find the value of ( cosecθ + secθ).
A) 2/3( 3+√3)
B) 1/3( 2+√3)
C) 2/5( 3+√5)
D) 1/5( 2+√3)
Answer A
Explanation
Let, θ=60°
Using value putting method,
6tanθ – 5√3secθ + 12cotθ
= 6tan60° -5√3sec60° + 12cot60°
= 6√3 – 5√3 ×2 + 12 × 1/√3
= 6√3 -10√3 +4√3
= 0
L.H.S = R.H.S (satisfied)
Now,
( cosec θ + sec θ)
=cosec 60°+sec 60° = 2/√3 + 2 = (2+2√3)/√3
= 2/3(3+√3)
Que 14. The average age of A, B and C is 20 years and that of B and C is 25 years. What is the age of A?
A) 15 years
B) 12 years
C) 10 years
D) 16 years
Answer C
Explanation
Total age of A, B and C = 20×3 = 60 years
Total age of B and C = 25×2 = 50 years
:. Age of A = (60-50) = 10 years
Que 15. The single discount equivalent to two successive discounts of 20% and 15% is –
A) 32%
B) 28%
C) 35%
D) 36%
Answer A
Explanation
Single discount = (x + y – xy/100)
= 20 +15 – (20×15)/100 %
= ( 35 – 3) %
= 32%
Que 16. Ram makes a profit of 30% by selling an article. What would be the profit if it were calculated on the selling price instead of the cost price? (Correct to one decimal place)
A) 20.2%
B) 23.1%
C) 25.5%
D) 18.3%
Answer B
Explanation
Cost price = 100
Profit percent = 30%
Selling price = 130
Now,
Profit per cent on selling price
= 30/130 × 100%
= 300/13 %
= 23.1%
Que 17. What is the area of a sector of a circle of radius 14 cm and a central angle of 45° ?( Take π=22/7)
A) 56 cm²
B) 60 cm²
C) 92 cm²
D) 77 cm²
Answer D
Explanation
Area of a sector of a circle
=πr²θ/360°
= 22/7×14²×45 ×1/360 = 77 cm²
Tricks:
If the radius is given in terms of a multiple of 7, then the area always be the multiple of 7.
Here only 77(option D) is the multiple of 7.
Que 18. Expand- (4a+3b+2c)²
A) 16a² + 9b² + 4c² + 24ab + 12bc + 16ca
B) 16a² + 9b² + 4c² – 24ab + 12bc + 16ca
C) 16a² + 9b² + 4c² – 24ab – 12bc + 16ca
D) 16a² + 9b² + 4c² – 24ab – 12bc – 16ca
Answer A
Explanation
(4a+3b+2c)²
= ( 4a+3b+2c)(4a+3b+2c)
= 4a(4a+3b+2c) + 3b(4a+3b+2c) +2c(4a+3b+2c)
= 16a²+12ab+8ca+12ab+9b²+6bc+8ca+6bc+4c²
= 16a²+9b²+4c²+24ab+12bc+16ca
Que 19. If A+B=12 and AB=17, what is the value of A³+B³?
A) 996
B) 1116
C) 1326
D) 1556
Answer B
Explanation
A³ + B³
= (A + B)(A² + B² – AB)
= (A + B){(A + B)² – 2AB – AB}
= 12 × { (12)² – 3 × 17}
= 12 × (144 – 51)
= 12 × 93
= 1116
Que 20. ∆PDC is drawn inside the square ABCD of side 24 cm where P lies on AB. What is the area of the triangle?
A) 144 cm²
B) 256 cm²
C) 288 cm²
D) 322 cm²
Answer C
Explanation
The base of the ∆PDC = Height of ∆PDC= side of square = 24 cm.
So, the Required area of ∆PDC = 1/2 ×base×height
= 1/2 × 24×24 cm²
= 288 cm²
Que 21. In the given figure, PA is a tangent from an external point P to the circle with centre o. If ∠POB=110°, then find the value of ∠APO.
A) 20°
B) 25°
C) 45°
D) 15°
Answer A
Explanation
∠POB + ∠POA = 180°
∠POA = 180° – 110° ( ∠POB= 110°)
:. ∠POA = 70°
∠PAO = 90°
Now,
∠POA + ∠APO + ∠PAO = 180°
=> 90° + ∠APO + 70° = 180°
=> ∠APO = 180° – 90° – 70°
:. ∠APO = 20°
IMPORTANT POINT: Tangent at any point of a circle is perpendicular to the radius at the point of contact. So, the tangent makes a right angle with the radius at the point of contact.
Que 22. Ravi scored 72% marks in an examination. If these are 360 marks, then the maximum marks are-
A) 400
B) 450
C) 500
D) 600
Answer C
Explanation
72% = 360
100% = 360/72 × 100 = 500
:. The maximum marks are 500.
Que 23. Ram and Shyam can complete a task in 20/3 days and 15 days respectively. They work together for 4 days and then Ram leaves. In how many days after Ram leaves, will Shyam complete the remaining task alone?
A) 4 days
B) 2 days
C) 5 days
D) 6 days
Answer B
Explanation
Ram = 20/3 days ; Shayam=15 days
Total work(L.C.M of 20/3,15) = 60
Ram’s 1 day work = 60×3/20 =9
Shyam’s 1 day work = 60/15 = 4
(Ram+Shyam)’s 4 days work = 4×(9+4) =52
Remaining work = (60-52) = 8
:. Remaining work done by Shyam alone = 8/4 = 2 days
Que 24. X and Y are two stations which are 280 km apart. A train starts at a certain time from X and travels towards Y at 60 km/h. After 2 hours, another train B starts from Y and travels towards X at 20 km/h. After how many hours does the train leaving from X meet the train which left from Y?
A) 4 hours
B) 6 hours
C) 3 hours
D) 2 hours
Answer A
Explanation
In 2 hours train A travels = 2×60 km = 120
Now, Distance should be covered by train A and train B = (280-120) = 160 km
Two trains are running in opposite direction so the relative speed = (60+20) km/h = 80 km/h
time = 160/80 = 2 hours
Since, train A is running 2 hours before the train B so,
The required time = 2+2 = 4 hours
Tricks :
Here,
D = 280 km , T = 2 hours , Speed 1 = 60 km/h , Speed 2 = 20 km/h
Required time = (D + TS1)/(S1 + S2)
= (280 + 2×20)/(60+20) = 320/80 = 4 hours
Que 25. (3a – 4b)³ is equal to-
A) 27a³ – 64b³
B) 9a² – 24ab + 16b²
C) 27a³ – 64b³ – 108a²b + 144ab²
D) 9a² – 16b²
Answer-C
Explanation-
(3a – 4b)³
= (3a)³ – 3 × (3a)² × 4b + 3 × 3a × (4b)² – (4b)³
= 27a³ – 108a²b + 144ab² – 64b³
= 27a³ – 64b³ – 108a²b + 144ab²
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...