Speed of a Travelling Wave
Last Updated :
29 Jul, 2021
In general, almost every material and object on earth has elastic binding forces. When the body is compressed or released, these elastic forces start acting and the motion of one part of the system affects other parts. Thus, the motion of one part of the system affects the other parts of the system too, thereby creating a disturbance that travels through the whole system in the form of a wave. For example, whenever pebbles are thrown in the water, waves are generated, and they travel in all directions. The objective here is to study these travelling waves and understand them better.
Waves
Waves are actual disturbances that move without the actual transfer of matter. These waves transport energy and the pattern of disturbance has information that propagates from one point to another. All the communications in our daily lives such as – phone signals, internet are actually waves of information that travel through different mediums to reach the users. These waves can be classified into two different categories on the basis of their way of propagating –
Transverse Waves – The particles of the medium oscillate perpendicular to the direction of motion of the wave.

Longitudinal Waves – The particles of the medium oscillate along the direction of propagation of motion of the wave.

Velocity of a Wave
Since the particles of the medium perform to and fro oscillation in the wave, these waves can be described mathematically in terms of trigonometric functions similar to simple harmonic motions (SHM). For convenience, the wave is considered to be a transverse wave, so that if the position of the constituents of the medium is denoted by x, the displacement from the equilibrium position can be denoted by y. Then, the sinusoidal wave can be represented by,
y(x, t) = Asin(kx – ωt)
Assume that the wave retains its shape as it moves. For a fixed point, the wave must have a constant argument to the sinusoidal function. Thus,
kx – ωt = constant
Therefore, differentiating it with time to find out the velocity.
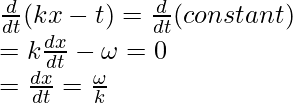
This equation represents the speed of the travelling wave. Let’s consider some special cases,
Speed of a transverse wave on a stretched string
In the case of a stretched string, the speed of the wave depends upon two factors – linear mass density per unit length and tension of the string. Linear mass density per unit length is defined as the mass per unit length for the string. Assuming that the tension in the wave is “T”. Then, the speed of the wave is given by,
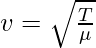
Speed of the sound wave in the air
It is known that sound travels in the form of compressions and rarefactions in the air. The property which determines the extent of compression and rarefactions in any medium is called Bulk Modulus(B). It is given by,
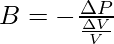
The above term represents how much change is volume is there on changing pressure at a finite value. The 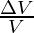 represents the fractional change in the volume on changing the pressure by
represents the fractional change in the volume on changing the pressure by 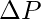 .
.
Therefore, the speed of the sound while travelling in a medium is given by,
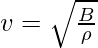
Where rho, represents the density of the medium.
Sample Problems
Question 1: Find the medium in which the waves will travel faster:
(1) H₂
(2) N2
(3) He
(4) O2
Answer:
The speed of the wave travelling in a medium is given by,
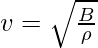
Notice that the speed of the wave is inversely proportional to the density of the medium.
Out of all the given options, the molecular mass of H₂ is the least for the equal volumes of gases. Thus, density for this medium is the least.
Therefore, the waves will travel fastest in the H₂.
Hence, answer is (1).
Question 2: Find the speed of the wave travelling a stretched string of tension T = 50N and mass density of 500g/m.
Answer:
The speed of the wave traveling in a string is given by,
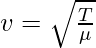
Here, T = 50N and μ = 500g/m.
Substituting the values in the equation,
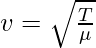
⇒ 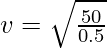
⇒ v = √100
⇒ v = 10 m/s.
Question 3: Find the speed of the wave traveling a stretched string of tension T = 100N and mass density of 2Kg/m.
Answer:
The speed of the wave traveling in a string is given by,
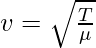
Here, T = 100N and μ = 2kg/m.
Substituting the values in the equation,
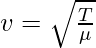
⇒ 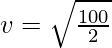
⇒ v = √50
⇒ v = 5√2 m/s.
Question 4: Find the speed of the wave traveling in a medium whose bulk modulus B is 1.01 × 105 N/m2and density is 1.29 Kg/m3.
Answer:
The speed of the wave travelling in a medium is given by,
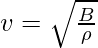
Here, B = 1.01 × 105 N/m2 and ρ = 1.29kg/m.
Substituting the values in the equation,
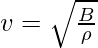
⇒ 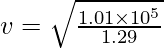
⇒ v = 280 m/s
Question 5: Find the speed of the wave travelling in a medium whose bulk modulus B is 6 × 106 N/m2and density is 1.5 Kg/m3.
Answer:
The speed of the wave travelling in a medium is given by,
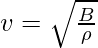
Here, B = 6 × 106 N/m2 and ρ = 1.5 kg/m.
Substituting the values in the equation,
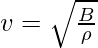
⇒ 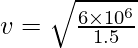
⇒ v = 400 m/s
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...