Mechanics can be termed as the branch of physics concerned with the concepts of energy and forces and their effect on bodies. It governs the relationships related to the motion of objects, that is, between matter, force, and its associated energy. It is responsible for the motion of bodies and the action of forces on these bodies as well. Practically, mechanics involve the design, construction, or operation of machines or tools. For instance, the distance covered by a car to stop travelling at a speed of 30 km/h.
The branch of classical mechanics concerned with the motion of points, object groups and systems, holding no reference to the motion of these objects, is called Kinematics, often termed the “Geometry of Motion.”
The sub-branch of physical science which is related to the motion of material objects under the effect of the physical factors affecting them, that is force, mass, momentum, and energy is called the Dynamics.
Rest
Anybody is said to be at a rest position if there is no change in its position (distance, displacement) with time, concerning its surroundings or a reference point.
Motion
The change in the position of anybody concerning time can be termed as motion. Any object under motion can be visualized by the naked eye by determining the change in the positional coordinates and then, associating it through the eye of the arbitrary observer. Motion can be computed in terms of both the position vectors, that is, the displacement, and distance, and taking into consideration the speed factors, that is, velocity, acceleration, speed, and time.
For instance, a spring ball attached to one end of a rod swinging at different time frames can be assumed to be in motion.

A rubber ball undergoing displacement under the influence of motion
Difference in Scalar and Vector
| Scalar
| Vector
|
Definition
| A physical quantity with only magnitude
| A physical quantity with both the magnitude and direction
|
Representation & Symbol
| A magnitude and Unit
| A number (magnitude) direction using a unit cap or arrow at the top and unit.
|
Direction
| No
| Yes
|
Examples
| Mass and Speed
| Velocity and Acceleration
|
Distance
Distance is the complete length of the path between any two successive points. The distance is a scalar quantity, with only magnitude and no associated direction. The distance is denoted by the symbol ‘d’. The distance of any object is considered to be a positive commodity. Distances can be measured both along the straight as well as zig-zag paths. The distance of a body gives the detailed route information that is followed while travelling from one point to another.
Distance = Speed x Time

Distance from location A to location B is 5 cm
Displacement
Displacement is the direct length of the minimum path between any two successive points. The displacement is a vector quantity, with both an associated magnitude and direction. It is denoted by ‘s’. The displacement of an object between any two points is considered to be positive, negative and even zero. Displacement is independent of the path and it only depends upon the initial and final position of the body. Therefore, it does not provide complete information on the route. Displacement is always indicated with an arrow.
Displacement = Velocity x Time

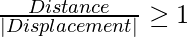
Speed
Speed can be defined as the rate of change of position of an object moving in any direction. Speed is measured as the ratio of the distance covered by an object to the time in which the distance was covered. The speed of any body is considered to be a scalar quantity, with only magnitude and no associated direction.

where, ‘s’ is the speed in m/s, ‘d’ is the distance travelled in m and t is the time taken in seconds.
| CGS system | cm/s |
| SI system | m/s |
Dimensional Formula for Speed
Mathematically,
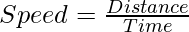
Dimensional formula for Distance = M0L1T0
Dimensional formula for time = M0L0T1
Therefore, dividing the dimensional formula for distance by the dimensional formula for time;
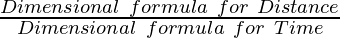
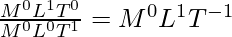
Hence,
The dimensional formula for speed = ML1T-1
Velocity
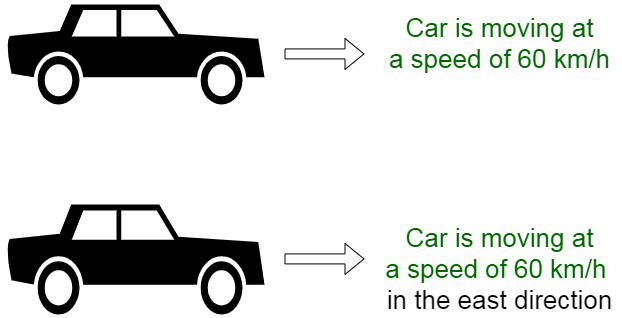
The velocity of an object can be defined as the rate of change of the object’s position concerning a frame of reference and time. The displacement is a vector quantity, with both an associated magnitude and direction. The SI unit is a meter per second (m/s). The velocity of an object can be positive, negative or even zero. If there is a change in magnitude or the direction in the velocity of a body the body is said to be accelerating.
Initial velocity describes the pace with which any object travels when gravity first applies force on the object, whereas, the final velocity is a vector quantity that describes the commodities of the speed and direction of a body in motion once it has reached its maximum acceleration.
Constant Velocity
Constant velocity can be termed as the motion in a straight line at a constant speed. Algebraically,
x = x0 + vt
where,
x0 represents the position of the object at
t = 0, and the slope of the line indicates the object’s speed.
The velocity can be positive or negative and is indicated by the sign of our slope. This tells us in which direction the object moves.

Constant Velocity Graph
Velocity Units
The S.I. unit of velocity is m/s (m/s).
Units and dimensions of velocity are as follows :
Units of velocity
|
SI unit
| m/s
|
Other units
| mph, ft/s
|
Dimension
| LT-1
|
Difference between Speed and Velocity
Speed
| Velocity
|
A quantitative measure of how quickly something is moving
| The direction of the movement of the body or the object.
|
Scalar quantity
| Vector quantity
|
It is the rate of change in distance
| It is the rate of change of displacement
|
The speed of an object moving can never be negative
| The velocity of a moving object can be zero.
|
Indicates the rapidity of the object.
| Indicates the position as well as the rapidity of the object.
|
Distance covered by an object in unit time.
| Displacement of the object in unit time.
|
Speed vs Velocity
Uniform Speed and Uniform Velocity
Uniform Speed
| Uniform Velocity
|
If an object covers equal distances in equal intervals of time, howsoever small these intervals of time may be.
| If an object covers equal displacements in equal intervals of time, howsoever small these intervals of time may be.
|
A motion with uniform speed can or cannot be a motion with uniform velocity.
| Motion with uniform velocity is also a motion with uniform speed.
|
| Scalar quantity | Variable quantity |
Variable Speed and Variable Velocity
| Variable Speed | Variable Velocity |
| Anybody covering unequal distances in equal intervals of time, even in the case of negligibly small time intervals. | Anybody covering unequal displacements in equal intervals of time, even in the case of negligibly small time intervals. |
| Scalar quantity | Vector quantity |
Instantaneous Velocity and Instantaneous Speed
Instantaneous speed is always greater than or equal to zero, that is it is a positive commodity. Instantaneous speed is a scalar quantity, associated with a magnitude and not direction. It is constant in case of uniform motion. It is a limit of the average speed for infinitely small time intervals.
Instantaneous velocity is an indicator of how fast an object is travelling at different instants of time within a given time interval. Also termed as average velocity for a negligibly small time interval. To summarise, the instantaneous speed at any given time interval is equivalent to the magnitude of instantaneous velocity at that time.
We have,
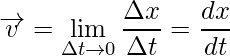
Here lim is taking operation of taking a limit with time tending towards 0 or infinitely small. And,  is the differential coefficient – Rate of change of position concerning time at an instant.
is the differential coefficient – Rate of change of position concerning time at an instant.

P-T graph for Instantaneous Velocities
From the graph, we have,
Slope P1P2 – Velocity at an instant of 3 sec
Slope Q1Q2 – Velocity at an instant of 1 sec
Whereas,
Instantaneous speed is referred to as the magnitude of velocity. The instantaneous speed at any instant in a time frame is equivalent to the magnitude of the instantaneous velocity at that particular instant. It is the rate with which the distance of any object changes concerning time.
The unit for speed is meters per second (m/s).
Now, we have,
Instantaneous speed (v) = 
v = limit as change in time approaches zero 
![Rendered by QuickLaTeX.com \displaystyle v=\lim_{\Delta t\rightarrow0}\frac{\Delta x}{\Delta t}\\ \displaystyle v=\lim_{\Delta t\rightarrow0}\frac{[x(t+\Delta t)]-x(t)}{\Delta t}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4198fd9fd0b364b21e60adf6884234e9_l3.png)
Where,
v = instantaneous speed (m/s)
Δ = change in values
x = displacement (m)
t = time (s)
Average Speed
The average speed of an object is the ratio of the total distance travelled by the object to the total time taken.
Average speed = 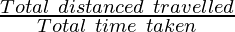
If a particle travels distances s1, s2, s3 , … with speeds v1, v2, v3, … respectively then,
Average speed = 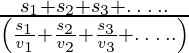
If any object travels equal distances during different time instances, (s1 = s2 = s) with velocities v1 and v2, then
Average speed = 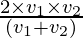
If any object travels with speeds v1, v2, v3, …, during time intervals t1, t2, t3,…, then,
Average speed = 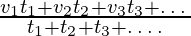
If any object travels with speeds v1, and v2 for equal time intervals, i.e., t1 = t2 = t3, then,
Average speed = 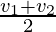
When a body travels an equal distance with speeds v1 and v2, the average speed, which is the harmonic mean of two speeds, is given by,
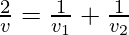
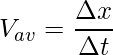
Calculating Average Speed
The total path length covered in unit time is called average speed.
Average Speed = 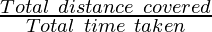
Average Velocity
The average velocity of any body is the ratio of total displacement to the total time taken. It is a vector quantity, with the same unit as the velocity. It is the rate with which an object changes its position from one place to another, in a time frame. Its standard unit is meters per second, but can also be convertible to other units such as miles per hour (mph) or kilometres per hour (mph).
Calculating Average Velocity
It is that single velocity with which the object can travel the same length in the same time as it generally does with varying velocity. The average speed of a body, at any specified time instance, is strictly greater than the magnitude of the average velocity.
Average Velocity = 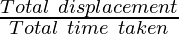
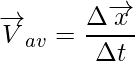

Difference in Average Velocity and Average Speed
Average Speed
| Average Velocity
|
Total path length travelled divided by total time interval regardless of direction.
| Change in position or displacement divided by time interval.
|
Average Speed = 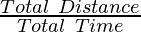
| Average Velocity = 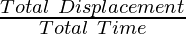
|
Scalar
| Vector
|
Always Positive
| Can be negative or positive
|
m/s
| m/s
|
Relative Velocity
The estimation of the velocity of an object about another object in the same time frame is known as relative velocity.
Let us consider, the relative velocity of object A concerning object B, to be
VAB = VA – VB
In case, the two objects are moving in the same direction, then
When two objects are moving in opposite directions, then
When two objects are moving at an angle, then
and
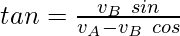
Examples on Speed and Velocity
Example 1. If a car goes a distance of 900 m in the west in 90 seconds. Find the speed and velocity of the distancethcarspeedaar.kilometres
Solution:
Here,
Distance = 900 m
Time = 90 s
Speed = 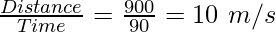
Velocity = 10 m/s to west
Example 2. If a car is moving with a. uniform speed covers a distance of 240 m in 6 seconds. Find the speed of the car and the time taken to cover a distance of 480 m.
Solution:
Here,
Distance = 240 m
Time = 6 sec
Speed of train ‘v’ = ?
Time taken by train to cover 480 m distance ‘t’ = ?
Speed = 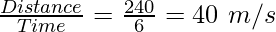
Time taken by the car to cover 480 m distance = 
Question 3. If a train travels from Delhi to Jaipur at the speed of 120 km/h and takes 3 hours to reach. Calculate the distance between the cities.then
Solution:
Here
Speed of the train ‘v’ = 120 km/h
Time taken ‘t’ = 3 hours
We have to find the Distance ‘s’ = ?
Distance = Speed × Time
= 120 × 3
= 360 km
Question 4. A boy throws a ball up in the air the ball rises about 50 m vertically in 2.5 seconds, thenit comes back to the boy in the same position in another 2.5 seconds. Calculate
(i) Distance travelled
(ii) Displacement
(iii) Average Speed
(iv) Average Velocity
Solution:
Here,
Distance travelled upwards = 50 m
Time taken = 2.5 seconds
(i) Total distance travelled = Distance travelled upward + Distance travelled downwards
= 50 + 50
= 100 m
(ii) Displacement = As the ball reaches to its initial point hence there will be zero displacement
= 0
(iii) Average Speed = 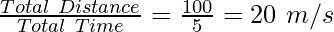
(iv) Average velocity = 0 {As the displacement is 0 thus the velocity is also 0}.
Example 5. If a car takes 4 hours to reach from Shimla to Chandigarh the speed has a . of 153 km from Shimla. If the car takes 5 hours for the return journey i.e. Chandigarh to Shimla. Calculate the average Speed and average Velocity of the car?
Solution:
Here,
Distance traveled in both the journeys s1, s2 = 153 km
Time taken for Shimla to Chandigarh t1 = 4 hours
Time taken for Chandigarh to Shimla t2 = 5 hours
We have to find average speed = ?
and average velocity = ?
Total Distance travelled = s1 + s2 = 153 km + 153 km = 306 km
Total Time taken = t + t = 4h + 5h = 9 h
Average Speed = 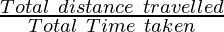
Average Speed = 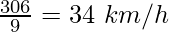
As the car reaches back to Shimla i.e starting point thus the displacement is zero.
Thus,
Average velocity = 0
Example 6. If a train driver has a. reaction time of 0.4 s between seeing the obstaclspeed. applying the brakes. Assume the train is travelling at a speed of 72 km/h and the driver spots the obstacle calculate the distance travelled before applying the brakes.the
Solution:
Here,
Reaction time ‘t’ = 0.4 s
Speed of the Train ‘v’ = 72 km/h or 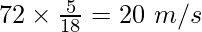
We have to find the distance travelled ‘s’ = ?
Distance = speed × time
Distance = 20 × 0.4
Distance = 8 m
Example 7. Assume a ball moves with velocity v in the direction of the mirror and the mirror moves with velocity v in the direction of the ball, So calculate the relative speed of the .ball’s image according to the ball?
Solution:
Velocity of the ball according to ground = v
Velocity of the mirror according to ground = v
Velocity of the ball’s image in the mirror according to = v
Image and ball both are moving towards each other so relative velocity will be = v+v = 2v.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...