Sparse Matrix Representations | Set 3 ( CSR )

If most of the elements in the matrix are zero then the matrix is called a sparse matrix. It is wasteful to store the zero elements in the matrix since they do not affect the results of our computation. This is why we implement these matrices in more efficient representations than the standard 2D Array. Using more efficient representations we can cut down space and time complexities of operations significantly.
We have discussed at 4 different representations in following articles : 

1. Sparse Matrix Representation | Set 1 
2. Sparse Matrix Representation | Set 2 .

In this article, we will discuss another representation of the Sparse Matrix which is commonly referred as the Yale Format.
The CSR (Compressed Sparse Row) or the Yale Format is similar to the Array Representation (discussed in Set 1) of Sparse Matrix. We represent a matrix M (m * n), by three 1-D arrays or vectors called as A, IA, JA. Let NNZ denote the number of non-zero elements in M and note that 0-based indexing is used. 

• The A vector is of size NNZ and it stores the values of the non-zero elements of the matrix. The values appear in the order of traversing the matrix row-by-row
• The IA vector is of size m+1 stores the cumulative number of non-zero elements upto ( not including) the i-th row. It is defined by the recursive relation : 
  • IA[0] = 0
  • IA[i] = IA[i-1] + no of non-zero elements in the (i-1) th row of the Matrix
• The JA vector stores the column index of each element in the A vector. Thus it is of size NNZ as well.

To find the no of non-zero elements in say row i, we perform IA[i+1] – IA[i]. Notice how this representation is different to the array based implementation where the second vector stores the row indices of non-zero elements.
The following examples show how these matrixes are represented.

Examples: 

Input : 0  0  0  0
        5  8  0  0
        0  0  3  0
        0  6  0  0

Solution: When the matrix is read row by 
          row, the A vector is [ 5 8 3 6]
          The JA vector stores column indices
          of elements in A hence, JA = [ 0 1 2 
           1]. IA[0] = 0. IA[1] = IA[0] + no  
          of non-zero elements in row 0 
          i.e 0 + 0 = 0.
          Similarly,
          IA[2] = IA[1] + 2 = 2
          IA[3] = IA[2] + 1 = 3  
          IA[4] = IA[3]+1 = 4
          Therefore IA = [0 0 2 3 4]
          The trick is remember that IA[i]
          stores NNZ upto and not-including 
          i row.

Input : 10  20  0  0  0  0
         0  30  0  4  0  0
         0   0 50 60 70  0
         0   0  0  0  0 80

Output :  A = [10 20 30 4 50 60 70 80],
         IA = [0 2 4 7 8]
         JA = [0  1 1 3 2 3 4 5]

Algorithm:

SPARSIFY (MATRIX)
Step 1: Set M to number of rows in MATRIX
Step 2: Set N to number of columns in MATRIX
Step 3: I = 0, NNZ = 0. Declare A, JA, and IA. 
        Set IA[0] to 0
Step 4: for I = 0 ... N-1
Step 5: for J = 0 ... N-1
Step 5: If MATRIX [I][J] is not zero
           Add MATRIX[I][J] to A
           Add J to JA
           NNZ = NNZ + 1
        [End of IF]
Step 6: [ End of J loop ]
        Add NNZ to IA
        [ End of I loop ]
Step 7: Print vectors A, IA, JA
Step 8: END

Implementation:

CPP

// CPP program to find sparse matrix rep-
// resentation using CSR
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

typedef std::vector<int> vi;

typedef vector<vector<int> > matrix;

// Utility Function to print a Matrix
void printMatrix(const matrix& M)
{
    int m = M.size();
    int n = M[0].size();
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++)
            cout << M[i][j] << " ";
        cout << endl;
    }
}

// Utility Function to print A, IA, JA vectors
// with some decoration.
void printVector(const vi& V, char* msg)
{

    cout << msg << "[ ";
    for_each(V.begin(), V.end(), [](int a) {
        cout << a << " ";
    });
    cout << "]" << endl;
}

// Generate the three vectors A, IA, JA
void sparesify(const matrix& M)
{
    int m = M.size();
    int n = M[0].size(), i, j;
    vi A;
    vi IA = { 0 }; // IA matrix has N+1 rows
    vi JA;
    int NNZ = 0;

    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) {
            if (M[i][j] != 0) {
                A.push_back(M[i][j]);
                JA.push_back(j);

                // Count Number of Non Zero
                // Elements in row i
                NNZ++;
            }
        }
        IA.push_back(NNZ);
    }

    printMatrix(M);
    printVector(A, (char*)"A = ");
    printVector(IA, (char*)"IA = ");
    printVector(JA, (char*)"JA = ");
}

// Driver code
int main()
{
    matrix M = {
        { 0, 0, 0, 0, 1 },
        { 5, 8, 0, 0, 0 },
        { 0, 0, 3, 0, 0 },
        { 0, 6, 0, 0, 1 },
    };

    sparesify(M);

    return 0;
}

Java

import java.util.*;

// Java program to find sparse matrix
// resentation using CSR

public class GFG {
    // Utility Function to print a Matrix
    private static void printMatrix(int[][] M)
    {
        int m = M.length;
        int n = (M.length == 0 ? 0 : M[0].length);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                System.out.print(M[i][j] + " ");
            }
            System.out.println();
        }
    }

    // Utility Function to print A, IA, JA vectors
    // with some decoration.
    private static void printVector(ArrayList<Integer> V,
                                    String msg)
    {

        System.out.print(msg + "[ ");
        for (var a : V) {
            System.out.print(a + " ");
        }
        System.out.println("]");
    }

    // Generate the three vectors A, IA, JA
    private static void sparesify(int[][] M)
    {
        int m = M.length;
        int n = (M.length == 0 ? 0 : M[0].length), i, j;
        ArrayList<Integer> A = new ArrayList<Integer>();
        ArrayList<Integer> IA
            = new ArrayList<Integer>(); // IA matrix has N+1
                                        // rows
        ArrayList<Integer> JA = new ArrayList<Integer>();
        int NNZ = 0;

        for (i = 0; i < m; i++) {
            for (j = 0; j < n; j++) {
                if (M[i][j] != 0) {
                    A.add(M[i][j]);
                    JA.add(j);

                    // Count Number of Non Zero
                    // Elements in row i
                    NNZ++;
                }
            }
            IA.add(NNZ);
        }

        printMatrix(M);
        printVector(A, "A = ");
        printVector(IA, "IA = ");
        printVector(JA, "JA = ");
    }

    // Driver code
    public static void main(String[] args)
    {
        int[][] M = { { 0, 0, 0, 0, 1 },
                      { 5, 8, 0, 0, 0 },
                      { 0, 0, 3, 0, 0 },
                      { 0, 6, 0, 0, 1 } };

        // Function call
        sparesify(M);
    }
}

// This code is contributed by Aarti_Rathi

C#

// C# program to find sparse matrix
// resentation using CSR

using System;
using System.Collections.Generic;

class GFG {
    // Utility Function to print a Matrix
    static void printMatrix(int[, ] M)
    {
        int m = M.GetLength(0);
        int n = M.GetLength(1);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++)
                Console.Write(M[i, j] + " ");
            Console.WriteLine();
        }
    }

    // Utility Function to print A, IA, JA vectors
    // with some decoration.
    static void printVector(List<int> V, string msg)
    {

        Console.Write(msg + "[ ");
        foreach(var a in V) { Console.Write(a + " "); }
        Console.WriteLine("]");
    }

    // Generate the three vectors A, IA, JA
    static void sparesify(int[, ] M)
    {
        int m = M.GetLength(0);
        int n = M.GetLength(1), i, j;
        List<int> A = new List<int>();
        List<int> IA
            = new List<int>(); // IA matrix has N+1 rows
        List<int> JA = new List<int>();
        int NNZ = 0;

        for (i = 0; i < m; i++) {
            for (j = 0; j < n; j++) {
                if (M[i, j] != 0) {
                    A.Add(M[i, j]);
                    JA.Add(j);

                    // Count Number of Non Zero
                    // Elements in row i
                    NNZ++;
                }
            }
            IA.Add(NNZ);
        }

        printMatrix(M);
        printVector(A, "A = ");
        printVector(IA, "IA = ");
        printVector(JA, "JA = ");
    }

    // Driver code
    public static void Main()
    {
        int[, ] M = {
            { 0, 0, 0, 0, 1 },
            { 5, 8, 0, 0, 0 },
            { 0, 0, 3, 0, 0 },
            { 0, 6, 0, 0, 1 },
        };

        // Function call
        sparesify(M);
    }
}

// This code is contributed by Aarti_Rathi

Python3

# Python 3 program to find sparse matrix
# resentation using CSR
class GFG :
    # Utility Function to print a Matrix
    @staticmethod
    def printMatrix( M) :
        m = len(M)
        n = (0 if len(M) == 0 else len(M[0]))
        i = 0
        while (i < m) :
            j = 0
            while (j < n) :
                print(str(M[i][j]) + " ", end ="")
                j += 1
            print()
            i += 1
    # Utility Function to print A, IA, JA vectors
    # with some decoration.
    @staticmethod
    def printVector( V,  msg) :
        print(msg + "[ ", end ="")
        for a in V :
            print(str(a) + " ", end ="")
        print("]")
    # Generate the three vectors A, IA, JA
    @staticmethod
    def sparesify( M) :
        m = len(M)
        n = (0 if len(M) == 0 else len(M[0]))
        i = 0
        j = 0
        A =  []
        IA =  []
        # IA matrix has N+1
        # rows
        JA =  []
        NNZ = 0
        i = 0
        while (i < m) :
            j = 0
            while (j < n) :
                if (M[i][j] != 0) :
                    A.append(M[i][j])
                    JA.append(j)
                    # Count Number of Non Zero
                    # Elements in row i
                    NNZ += 1
                j += 1
            IA.append(NNZ)
            i += 1
        GFG.printMatrix(M)
        GFG.printVector(A, "A = ")
        GFG.printVector(IA, "IA = ")
        GFG.printVector(JA, "JA = ")
    # Driver code
    @staticmethod
    def main( args) :
        M = [[0, 0, 0, 0, 1], [5, 8, 0, 0, 0], [0, 0, 3, 0, 0], [0, 6, 0, 0, 1]]
        # Function call
        GFG.sparesify(M)


if __name__=="__main__":
    GFG.main([])

Javascript

// JS program to find sparse matrix
// resentation using CSR

class GFG
{
    // Utility Function to print a Matrix
    printMatrix( M)
    {
        let m = M.length
        let n =  (m == 0) ? 0 : M[0].length
        let i = 0
        while (i < m)
        {
            let j = 0
            while (j < n)
            {
                process.stdout.write((M[i][j]) + " ")
                j += 1
            }
            console.log()
            i += 1
        }
    }
    // Utility Function to print A, IA, JA vectors
    // with some decoration.
    printVector( V,  msg)
    {
        process.stdout.write(msg + "[ ")
        process.stdout.write(V.join(" ") )

        console.log("]")
    }
    // Generate the three vectors A, IA, JA
    sparesify( M)
    {
        let m = M.length
        let n =  (m == 0) ? 0 : M[0].length
        let j = 0
        let A =  []
        let IA =  []
        // IA matrix has N+1
        // rows
        let JA =  []
        let NNZ = 0
        let i = 0
        while (i < m)
        {
            j = 0
            while (j < n)
            {
                if (M[i][j] != 0)
                {
                    A.push(M[i][j])
                    JA.push(j)
                    // Count Number of Non Zero
                    // Elements in row i
                    NNZ += 1
                }
                j += 1
            }
            IA.push(NNZ)
            i += 1
        }
        g.printMatrix(M)
        g.printVector(A, "A = ")
        g.printVector(IA, "IA = ")
        g.printVector(JA, "JA = ")


    }
}
// Driver code
let M = [[0, 0, 0, 0, 1], [5, 8, 0, 0, 0], [0, 0, 3, 0, 0], [0, 6, 0, 0, 1]]

// Function call
let g = new GFG()
g.sparesify(M)

 // This code is contributed by phasing17.

Output

0 0 0 0 1 
5 8 0 0 0 
0 0 3 0 0 
0 6 0 0 1 
A = [ 1 5 8 3 6 1 ]
IA = [ 0 1 3 4 6 ]
JA = [ 4 0 1 2 1 4 ]

Time Complexity : O(n x m)
Auxiliary Space: O(n + m)

Notes 

• The sparsity of the matrix = ( Total No of Elements – Number of Non Zero Elements) / ( Total No of Elements) or (1 – NNZ/mn ) or ( 1 – size(A)/mn ) .
• The direct array based representation required memory 3 * NNZ while CSR requires ( 2*NNZ + m + 1) memory.
• CSR matrices are memory efficient as long as .
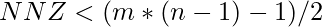• Similar to CSR there exits CSC which stands for Compressed Sparse Columns. It is the column analogue for CSR.
• The ‘New’ Yale format further compresses the A and JA vectors into 1 vector.

 This article is contributed by Aarti_Rathi. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.