Sparse Matrix Representations | Set 3 ( CSR )
Last Updated :
29 Nov, 2022
If most of the elements in the matrix are zero then the matrix is called a sparse matrix. It is wasteful to store the zero elements in the matrix since they do not affect the results of our computation. This is why we implement these matrices in more efficient representations than the standard 2D Array. Using more efficient representations we can cut down space and time complexities of operations significantly.
We have discussed at 4 different representations in following articles :
- Sparse Matrix Representation | Set 1
- Sparse Matrix Representation | Set 2 .
In this article, we will discuss another representation of the Sparse Matrix which is commonly referred as the Yale Format.
The CSR (Compressed Sparse Row) or the Yale Format is similar to the Array Representation (discussed in Set 1) of Sparse Matrix. We represent a matrix M (m * n), by three 1-D arrays or vectors called as A, IA, JA. Let NNZ denote the number of non-zero elements in M and note that 0-based indexing is used.
- The A vector is of size NNZ and it stores the values of the non-zero elements of the matrix. The values appear in the order of traversing the matrix row-by-row
- The IA vector is of size m+1 stores the cumulative number of non-zero elements upto ( not including) the i-th row. It is defined by the recursive relation :
- IA[0] = 0
- IA[i] = IA[i-1] + no of non-zero elements in the (i-1) th row of the Matrix
- The JA vector stores the column index of each element in the A vector. Thus it is of size NNZ as well.
To find the no of non-zero elements in say row i, we perform IA[i+1] – IA[i]. Notice how this representation is different to the array based implementation where the second vector stores the row indices of non-zero elements.
The following examples show how these matrixes are represented.
Examples:
Input : 0 0 0 0
5 8 0 0
0 0 3 0
0 6 0 0
Solution: When the matrix is read row by
row, the A vector is [ 5 8 3 6]
The JA vector stores column indices
of elements in A hence, JA = [ 0 1 2
1]. IA[0] = 0. IA[1] = IA[0] + no
of non-zero elements in row 0
i.e 0 + 0 = 0.
Similarly,
IA[2] = IA[1] + 2 = 2
IA[3] = IA[2] + 1 = 3
IA[4] = IA[3]+1 = 4
Therefore IA = [0 0 2 3 4]
The trick is remember that IA[i]
stores NNZ upto and not-including
i row.
Input : 10 20 0 0 0 0
0 30 0 4 0 0
0 0 50 60 70 0
0 0 0 0 0 80
Output : A = [10 20 30 4 50 60 70 80],
IA = [0 2 4 7 8]
JA = [0 1 1 3 2 3 4 5]
Algorithm:
SPARSIFY (MATRIX)
Step 1: Set M to number of rows in MATRIX
Step 2: Set N to number of columns in MATRIX
Step 3: I = 0, NNZ = 0. Declare A, JA, and IA.
Set IA[0] to 0
Step 4: for I = 0 ... N-1
Step 5: for J = 0 ... N-1
Step 5: If MATRIX [I][J] is not zero
Add MATRIX[I][J] to A
Add J to JA
NNZ = NNZ + 1
[End of IF]
Step 6: [ End of J loop ]
Add NNZ to IA
[ End of I loop ]
Step 7: Print vectors A, IA, JA
Step 8: END
Implementation:
CPP
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
typedef std::vector<int> vi;
typedef vector<vector<int> > matrix;
void printMatrix(const matrix& M)
{
int m = M.size();
int n = M[0].size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++)
cout << M[i][j] << " ";
cout << endl;
}
}
void printVector(const vi& V, char* msg)
{
cout << msg << "[ ";
for_each(V.begin(), V.end(), [](int a) {
cout << a << " ";
});
cout << "]" << endl;
}
void sparesify(const matrix& M)
{
int m = M.size();
int n = M[0].size(), i, j;
vi A;
vi IA = { 0 };
vi JA;
int NNZ = 0;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
if (M[i][j] != 0) {
A.push_back(M[i][j]);
JA.push_back(j);
NNZ++;
}
}
IA.push_back(NNZ);
}
printMatrix(M);
printVector(A, (char*)"A = ");
printVector(IA, (char*)"IA = ");
printVector(JA, (char*)"JA = ");
}
int main()
{
matrix M = {
{ 0, 0, 0, 0, 1 },
{ 5, 8, 0, 0, 0 },
{ 0, 0, 3, 0, 0 },
{ 0, 6, 0, 0, 1 },
};
sparesify(M);
return 0;
}
|
Java
import java.util.*;
public class GFG {
private static void printMatrix(int[][] M)
{
int m = M.length;
int n = (M.length == 0 ? 0 : M[0].length);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(M[i][j] + " ");
}
System.out.println();
}
}
private static void printVector(ArrayList<Integer> V,
String msg)
{
System.out.print(msg + "[ ");
for (var a : V) {
System.out.print(a + " ");
}
System.out.println("]");
}
private static void sparesify(int[][] M)
{
int m = M.length;
int n = (M.length == 0 ? 0 : M[0].length), i, j;
ArrayList<Integer> A = new ArrayList<Integer>();
ArrayList<Integer> IA
= new ArrayList<Integer>();
ArrayList<Integer> JA = new ArrayList<Integer>();
int NNZ = 0;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
if (M[i][j] != 0) {
A.add(M[i][j]);
JA.add(j);
NNZ++;
}
}
IA.add(NNZ);
}
printMatrix(M);
printVector(A, "A = ");
printVector(IA, "IA = ");
printVector(JA, "JA = ");
}
public static void main(String[] args)
{
int[][] M = { { 0, 0, 0, 0, 1 },
{ 5, 8, 0, 0, 0 },
{ 0, 0, 3, 0, 0 },
{ 0, 6, 0, 0, 1 } };
sparesify(M);
}
}
|
C#
using System;
using System.Collections.Generic;
class GFG {
static void printMatrix(int[, ] M)
{
int m = M.GetLength(0);
int n = M.GetLength(1);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++)
Console.Write(M[i, j] + " ");
Console.WriteLine();
}
}
static void printVector(List<int> V, string msg)
{
Console.Write(msg + "[ ");
foreach(var a in V) { Console.Write(a + " "); }
Console.WriteLine("]");
}
static void sparesify(int[, ] M)
{
int m = M.GetLength(0);
int n = M.GetLength(1), i, j;
List<int> A = new List<int>();
List<int> IA
= new List<int>();
List<int> JA = new List<int>();
int NNZ = 0;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
if (M[i, j] != 0) {
A.Add(M[i, j]);
JA.Add(j);
NNZ++;
}
}
IA.Add(NNZ);
}
printMatrix(M);
printVector(A, "A = ");
printVector(IA, "IA = ");
printVector(JA, "JA = ");
}
public static void Main()
{
int[, ] M = {
{ 0, 0, 0, 0, 1 },
{ 5, 8, 0, 0, 0 },
{ 0, 0, 3, 0, 0 },
{ 0, 6, 0, 0, 1 },
};
sparesify(M);
}
}
|
Python3
class GFG :
@staticmethod
def printMatrix( M) :
m = len(M)
n = (0 if len(M) == 0 else len(M[0]))
i = 0
while (i < m) :
j = 0
while (j < n) :
print(str(M[i][j]) + " ", end ="")
j += 1
print()
i += 1
@staticmethod
def printVector( V, msg) :
print(msg + "[ ", end ="")
for a in V :
print(str(a) + " ", end ="")
print("]")
@staticmethod
def sparesify( M) :
m = len(M)
n = (0 if len(M) == 0 else len(M[0]))
i = 0
j = 0
A = []
IA = []
JA = []
NNZ = 0
i = 0
while (i < m) :
j = 0
while (j < n) :
if (M[i][j] != 0) :
A.append(M[i][j])
JA.append(j)
NNZ += 1
j += 1
IA.append(NNZ)
i += 1
GFG.printMatrix(M)
GFG.printVector(A, "A = ")
GFG.printVector(IA, "IA = ")
GFG.printVector(JA, "JA = ")
@staticmethod
def main( args) :
M = [[0, 0, 0, 0, 1], [5, 8, 0, 0, 0], [0, 0, 3, 0, 0], [0, 6, 0, 0, 1]]
GFG.sparesify(M)
if __name__=="__main__":
GFG.main([])
|
Javascript
class GFG
{
printMatrix( M)
{
let m = M.length
let n = (m == 0) ? 0 : M[0].length
let i = 0
while (i < m)
{
let j = 0
while (j < n)
{
process.stdout.write((M[i][j]) + " ")
j += 1
}
console.log()
i += 1
}
}
printVector( V, msg)
{
process.stdout.write(msg + "[ ")
process.stdout.write(V.join(" ") )
console.log("]")
}
sparesify( M)
{
let m = M.length
let n = (m == 0) ? 0 : M[0].length
let j = 0
let A = []
let IA = []
let JA = []
let NNZ = 0
let i = 0
while (i < m)
{
j = 0
while (j < n)
{
if (M[i][j] != 0)
{
A.push(M[i][j])
JA.push(j)
NNZ += 1
}
j += 1
}
IA.push(NNZ)
i += 1
}
g.printMatrix(M)
g.printVector(A, "A = ")
g.printVector(IA, "IA = ")
g.printVector(JA, "JA = ")
}
}
let M = [[0, 0, 0, 0, 1], [5, 8, 0, 0, 0], [0, 0, 3, 0, 0], [0, 6, 0, 0, 1]]
let g = new GFG()
g.sparesify(M)
|
Output0 0 0 0 1
5 8 0 0 0
0 0 3 0 0
0 6 0 0 1
A = [ 1 5 8 3 6 1 ]
IA = [ 0 1 3 4 6 ]
JA = [ 4 0 1 2 1 4 ]
Time Complexity : O(n x m)
Auxiliary Space: O(n + m)
Notes
- The sparsity of the matrix = ( Total No of Elements – Number of Non Zero Elements) / ( Total No of Elements) or (1 – NNZ/mn ) or ( 1 – size(A)/mn ) .
- The direct array based representation required memory 3 * NNZ while CSR requires ( 2*NNZ + m + 1) memory.
- CSR matrices are memory efficient as long as
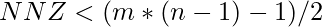 .
. - Similar to CSR there exits CSC which stands for Compressed Sparse Columns. It is the column analogue for CSR.
- The ‘New’ Yale format further compresses the A and JA vectors into 1 vector.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...