Sparse Matrix and its representations | Set 1 (Using Arrays and Linked Lists)

A matrix is a two-dimensional data object made of m rows and n columns, therefore having total m x n values. If most of the elements of the matrix have 0 value, then it is called a sparse matrix.

Why to use Sparse Matrix instead of simple matrix ?

• Storage: There are lesser non-zero elements than zeros and thus lesser memory can be used to store only those elements.
• Computing time: Computing time can be saved by logically designing a data structure traversing only non-zero elements..

Example: 

0 0 3 0 4            
0 0 5 7 0
0 0 0 0 0
0 2 6 0 0

Representing a sparse matrix by a 2D array leads to wastage of lots of memory as zeroes in the matrix are of no use in most of the cases. So, instead of storing zeroes with non-zero elements, we only store non-zero elements. This means storing non-zero elements with triples- (Row, Column, value).

Sparse Matrix Representations can be done in many ways following are two common representations: 

1. Array representation
2. Linked list representation

Method 1: Using Arrays:

2D array is used to represent a sparse matrix in which there are three rows named as 

• Row: Index of row, where non-zero element is located
• Column: Index of column, where non-zero element is located
• Value: Value of the non zero element located at index – (row,column)

Implementation:

C++

// C++ program for Sparse Matrix Representation
// using Array
#include <iostream>
using namespace std;

int main()
{
    // Assume 4x5 sparse matrix
    int sparseMatrix[4][5] =
    {
        {0 , 0 , 3 , 0 , 4 },
        {0 , 0 , 5 , 7 , 0 },
        {0 , 0 , 0 , 0 , 0 },
        {0 , 2 , 6 , 0 , 0 }
    };

    int size = 0;
    for (int i = 0; i < 4; i++)
        for (int j = 0; j < 5; j++)
            if (sparseMatrix[i][j] != 0)
                size++;

    // number of columns in compactMatrix (size) must be
    // equal to number of non - zero elements in
    // sparseMatrix
    int compactMatrix[3][size];

    // Making of new matrix
    int k = 0;
    for (int i = 0; i < 4; i++)
        for (int j = 0; j < 5; j++)
            if (sparseMatrix[i][j] != 0)
            {
                compactMatrix[0][k] = i;
                compactMatrix[1][k] = j;
                compactMatrix[2][k] = sparseMatrix[i][j];
                k++;
            }

    for (int i=0; i<3; i++)
    {
        for (int j=0; j<size; j++)
            cout <<" "<< compactMatrix[i][j];

        cout <<"\n";
    }
    return 0;
}

// this code is contributed by shivanisinghss2110

C

// C++ program for Sparse Matrix Representation
// using Array
#include<stdio.h>

int main()
{
    // Assume 4x5 sparse matrix
    int sparseMatrix[4][5] =
    {
        {0 , 0 , 3 , 0 , 4 },
        {0 , 0 , 5 , 7 , 0 },
        {0 , 0 , 0 , 0 , 0 },
        {0 , 2 , 6 , 0 , 0 }
    };

    int size = 0;
    for (int i = 0; i < 4; i++)
        for (int j = 0; j < 5; j++)
            if (sparseMatrix[i][j] != 0)
                size++;

    // number of columns in compactMatrix (size) must be
    // equal to number of non - zero elements in
    // sparseMatrix
    int compactMatrix[3][size];

    // Making of new matrix
    int k = 0;
    for (int i = 0; i < 4; i++)
        for (int j = 0; j < 5; j++)
            if (sparseMatrix[i][j] != 0)
            {
                compactMatrix[0][k] = i;
                compactMatrix[1][k] = j;
                compactMatrix[2][k] = sparseMatrix[i][j];
                k++;
            }

    for (int i=0; i<3; i++)
    {
        for (int j=0; j<size; j++)
            printf("%d ", compactMatrix[i][j]);

        printf("\n");
    }
    return 0;
}

Java

// Java program for Sparse Matrix Representation
// using Array
class GFG
{

    public static void main(String[] args)
    {
        int sparseMatrix[][]
                = {
                    {0, 0, 3, 0, 4},
                    {0, 0, 5, 7, 0},
                    {0, 0, 0, 0, 0},
                    {0, 2, 6, 0, 0}
                };

        int size = 0;
        for (int i = 0; i < 4; i++)
        {
            for (int j = 0; j < 5; j++)
            {
                if (sparseMatrix[i][j] != 0)
                {
                    size++;
                }
            }
        }

        // number of columns in compactMatrix (size) must be
        // equal to number of non - zero elements in
        // sparseMatrix
        int compactMatrix[][] = new int[3][size];

        // Making of new matrix
        int k = 0;
        for (int i = 0; i < 4; i++)
        {
            for (int j = 0; j < 5; j++)
            {
                if (sparseMatrix[i][j] != 0)
                {
                    compactMatrix[0][k] = i;
                    compactMatrix[1][k] = j;
                    compactMatrix[2][k] = sparseMatrix[i][j];
                    k++;
                }
            }
        }

        for (int i = 0; i < 3; i++)
        {
            for (int j = 0; j < size; j++)
            {
                System.out.printf("%d ", compactMatrix[i][j]);
            }
            System.out.printf("\n");
        }
    }
}

/* This code contributed by PrinciRaj1992 */

Python3

# Python program for Sparse Matrix Representation
# using arrays

# assume a sparse matrix of order 4*5
# let assume another matrix compactMatrix
# now store the value,row,column of arr1 in sparse matrix compactMatrix

sparseMatrix = [[0,0,3,0,4],[0,0,5,7,0],[0,0,0,0,0],[0,2,6,0,0]]

# initialize size as 0
size = 0

for i in range(4):
    for j in range(5):
        if (sparseMatrix[i][j] != 0):
            size += 1

# number of columns in compactMatrix(size) should
# be equal to number of non-zero elements in sparseMatrix
rows, cols = (3, size)
compactMatrix = [[0 for i in range(cols)] for j in range(rows)]

k = 0
for i in range(4):
    for j in range(5):
        if (sparseMatrix[i][j] != 0):
            compactMatrix[0][k] = i
            compactMatrix[1][k] = j
            compactMatrix[2][k] = sparseMatrix[i][j]
            k += 1

for i in compactMatrix:
    print(i)

# This code is contributed by MRINALWALIA

C#

// C# program for Sparse Matrix Representation
// using Array

using System;

class Program {
    static void Main(string[] args)
    {
        // Assume 4x5 sparse matrix
        int[, ] sparseMatrix
            = new int[4, 5] { { 0, 0, 3, 0, 4 },
                              { 0, 0, 5, 7, 0 },
                              { 0, 0, 0, 0, 0 },
                              { 0, 2, 6, 0, 0 } };
        int size = 0;
        for (int i = 0; i < 4; i++)
            for (int j = 0; j < 5; j++)
                if (sparseMatrix[i, j] != 0)
                    size++;

        // number of columns in compactMatrix (size) must be
        // equal to number of non - zero elements in
        // sparseMatrix
        int[, ] compactMatrix = new int[3, size];

        // Making of new matrix
        int k = 0;
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 5; j++)
                if (sparseMatrix[i, j] != 0) {
                    compactMatrix[0, k] = i;
                    compactMatrix[1, k] = j;
                    compactMatrix[2, k]
                        = sparseMatrix[i, j];
                    k++;
                }
        }

        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < size; j++)
                Console.Write(" " + compactMatrix[i, j]);
            Console.WriteLine();
        }
    }
}
// This code is contributed by Tapesh(tapeshdua420)

Javascript

//JS  program for Sparse Matrix Representation
// using Array

    // Assume 4x5 sparse matrix
    let sparseMatrix =
    [
        [0 , 0 , 3 , 0 , 4 ],
        [0 , 0 , 5 , 7 , 0 ],
        [0 , 0 , 0 , 0 , 0 ],
        [0 , 2 , 6 , 0 , 0 ]
    ];

    let size = 0;
    for (let i = 0; i < 4; i++)
        for (let j = 0; j < 5; j++)
            if (sparseMatrix[i][j] != 0)
                size++;

    // number of columns in compactMatrix (size) must be
    // equal to number of non - zero elements in
    // sparseMatrix
    let compactMatrix = new Array(3);
    for (var i = 0; i < 3; i++)
        compactMatrix[i] = new Array(size);


    // Making of new matrix
    let k = 0;
    for (let i = 0; i < 4; i++)
        for (let j = 0; j < 5; j++)
            if (sparseMatrix[i][j] != 0)
            {
                compactMatrix[0][k] = i;
                compactMatrix[1][k] = j;
                compactMatrix[2][k] = sparseMatrix[i][j];
                k++;
            }

    for (let i=0; i<3; i++)
    {
        for (let j=0; j<size; j++)
            process.stdout.write(" " + compactMatrix[i][j]);

        console.log()
    }


// this code is contributed by phasing17

Output

 0 0 1 1 3 3
 2 4 2 3 1 2
 3 4 5 7 2 6

Time Complexity:  O(NM), where N is the number of rows in the sparse matrix, and M is the number of columns in the sparse matrix.

Auxiliary Space: O(NM), where N is the number of rows in the sparse matrix, and M is the number of columns in the sparse matrix.

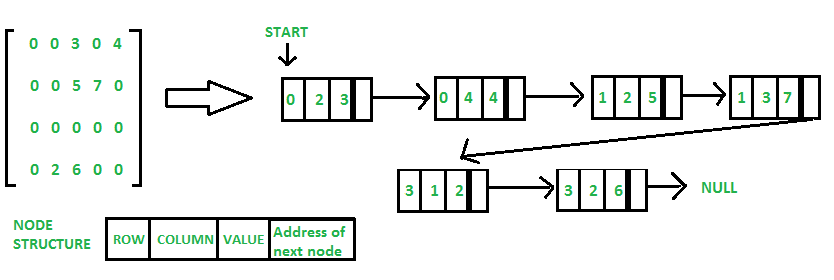
Method 2: Using Linked Lists
In linked list, each node has four fields. These four fields are defined as: 

• Row: Index of row, where non-zero element is located
• Column: Index of column, where non-zero element is located
• Value: Value of the non zero element located at index – (row,column)
• Next node: Address of the next node

C++

// C++ program for sparse matrix representation.
// Using Link list
#include<iostream>
using namespace std;

// Node class to represent link list
class Node
{
    public:
    int row;
    int col;
    int data;
    Node *next;
};

// Function to create new node
void create_new_node(Node **p, int row_index,
                     int col_index, int x)
{
    Node *temp = *p;
    Node *r;

    // If link list is empty then
    // create first node and assign value.
    if (temp == NULL)
    {
        temp = new Node();
        temp->row = row_index;
        temp->col = col_index;
        temp->data = x;
        temp->next = NULL;
        *p = temp;
    }

    // If link list is already created
    // then append newly created node
    else
    {
        while (temp->next != NULL)
            temp = temp->next;

        r = new Node();
        r->row = row_index;
        r->col = col_index;
        r->data = x;
        r->next = NULL;
        temp->next = r;
    }
}

// Function prints contents of linked list
// starting from start
void printList(Node *start)
{
    Node *ptr = start;
    cout << "row_position:";
    while (ptr != NULL)
    {
        cout << ptr->row << " ";
        ptr = ptr->next;
    }
    cout << endl;
    cout << "column_position:";

    ptr = start;
    while (ptr != NULL)
    {
        cout << ptr->col << " ";
        ptr = ptr->next;
    }
    cout << endl;
    cout << "Value:";
    ptr = start;

    while (ptr != NULL)
    {
        cout << ptr->data << " ";
        ptr = ptr->next;
    }
}

// Driver Code
int main()
{

    // 4x5 sparse matrix
    int sparseMatrix[4][5] = { { 0 , 0 , 3 , 0 , 4 },
                               { 0 , 0 , 5 , 7 , 0 },
                               { 0 , 0 , 0 , 0 , 0 },
                               { 0 , 2 , 6 , 0 , 0 } };

    // Creating head/first node of list as NULL
    Node *first = NULL;
    for(int i = 0; i < 4; i++)
    {
        for(int j = 0; j < 5; j++)
        {

            // Pass only those values which
            // are non - zero
            if (sparseMatrix[i][j] != 0)
                create_new_node(&first, i, j,
                                sparseMatrix[i][j]);
        }
    }
    printList(first);

    return 0;
}

// This code is contributed by ronaksuba

C

// C program for Sparse Matrix Representation
// using Linked Lists
#include<stdio.h>
#include<stdlib.h>

// Node to represent sparse matrix
struct Node
{
    int value;
    int row_position;
    int column_postion;
    struct Node *next;
};

// Function to create new node
void create_new_node(struct Node** start, int non_zero_element,
                     int row_index, int column_index )
{
    struct Node *temp, *r;
    temp = *start;
    if (temp == NULL)
    {
        // Create new node dynamically
        temp = (struct Node *) malloc (sizeof(struct Node));
        temp->value = non_zero_element;
        temp->row_position = row_index;
        temp->column_postion = column_index;
        temp->next = NULL;
        *start = temp;

    }
    else
    {
        while (temp->next != NULL)
            temp = temp->next;

        // Create new node dynamically
        r = (struct Node *) malloc (sizeof(struct Node));
        r->value = non_zero_element;
        r->row_position = row_index;
        r->column_postion = column_index;
        r->next = NULL;
        temp->next = r;

    }
}

// This function prints contents of linked list
// starting from start
void PrintList(struct Node* start)
{
    struct Node *temp, *r, *s;
    temp = r = s = start;

    printf("row_position: ");
    while(temp != NULL)
    {

        printf("%d ", temp->row_position);
        temp = temp->next;
    }
    printf("\n");

    printf("column_postion: ");
    while(r != NULL)
    {
        printf("%d ", r->column_postion);
        r = r->next;
    }
    printf("\n");
    printf("Value: ");
    while(s != NULL)
    {
        printf("%d ", s->value);
        s = s->next;
    }
    printf("\n");
}


// Driver of the program
int main()
{
   // Assume 4x5 sparse matrix
    int sparseMatric[4][5] =
    {
        {0 , 0 , 3 , 0 , 4 },
        {0 , 0 , 5 , 7 , 0 },
        {0 , 0 , 0 , 0 , 0 },
        {0 , 2 , 6 , 0 , 0 }
    };

    /* Start with the empty list */
    struct Node* start = NULL;

    for (int i = 0; i < 4; i++)
        for (int j = 0; j < 5; j++)

            // Pass only those values which are non - zero
            if (sparseMatric[i][j] != 0)
                create_new_node(&start, sparseMatric[i][j], i, j);

    PrintList(start);

    return 0;
}

Java

// Java program for sparse matrix representation.
// Using Link list
import java.util.*;

public class SparseMatrix {
    // Creating head/first node of list as NULL
    static Node first = null;

    // Node class to represent link list
    public static class Node {
        int row;
        int col;
        int data;
        Node next;
    };

    // Driver Code
    public static void main(String[] args)
    {
        // 4x5 sparse matrix
        int[][] sparseMatrix = { { 0, 0, 3, 0, 4 },
                                 { 0, 0, 5, 7, 0 },
                                 { 0, 0, 0, 0, 0 },
                                 { 0, 2, 6, 0, 0 } };

        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 5; j++) {
                // Pass only those values which
                // are non - zero
                if (sparseMatrix[i][j] != 0) {
                    create_new_node(i, j,
                                    sparseMatrix[i][j]);
                }
            }
        }
        printList(first);
    }
    // Function to create new node
    private static void
    create_new_node(int row_index, int col_index, int x)
    {
        Node temp = first;
        Node r;

        // If link list is empty then
        // create first node and assign value.
        if (temp == null) {
            temp = new Node();
            temp.row = row_index;
            temp.col = col_index;
            temp.data = x;
            temp.next = null;
            first = temp;
        }

        // If link list is already created
        // then append newly created node
        else {
            while (temp.next != null)
                temp = temp.next;

            r = new Node();
            r.row = row_index;
            r.col = col_index;
            r.data = x;
            r.next = null;
            temp.next = r;
        }
    }

    // Function prints contents of linked list
    // starting from start
    public static void printList(Node start)
    {
        Node ptr = start;
        System.out.print("row_position:");
        while (ptr != null) {
            System.out.print(ptr.row + " ");
            ptr = ptr.next;
        }
        System.out.println("");
        System.out.print("column_position:");

        ptr = start;
        while (ptr != null) {
            System.out.print(ptr.col + " ");
            ptr = ptr.next;
        }
        System.out.println("");
        System.out.print("Value:");
        ptr = start;

        while (ptr != null) {
            System.out.print(ptr.data + " ");
            ptr = ptr.next;
        }
    }
}

// This code is contributed by Tapesh (tapeshdua420)

Python3

# Python Program for Representation of
# Sparse Matrix using Linked List

# Node Class to represent Linked List Node
class Node:

    # Making the slots for storing row,
    # column, value, and address
    __slots__ = "row", "col", "data", "next"

    # Constructor to initialize the values
    def __init__(self, row=0, col=0, data=0, next=None):

        self.row = row
        self.col = col
        self.data = data
        self.next = next


# Class to convert Sparse Matrix
# into Linked List
class Sparse:

    # Initialize Class Variables
    def __init__(self):
        self.head = None
        self.temp = None
        self.size = 0

    # Function which returns the size
    # of the Linked List
    def __len__(self):
        return self.size

    # Check the Linked List is
    # Empty or not
    def isempty(self):
        return self.size == 0

    # Responsible function to create
    # Linked List from Sparse Matrix
    def create_new_node(self, row, col, data):

        # Creating New Node
        newNode = Node(row, col, data, None)

        # Check whether the List is
        # empty or not
        if self.isempty():
            self.head = newNode
        else:
            self.temp.next = newNode
        self.temp = newNode

        # Incrementing the size
        self.size += 1

    # Function display the contents of
    # Linked List
    def PrintList(self):
        temp = r = s = self.head
        print("row_position:", end=" ")
        while temp != None:
            print(temp.row, end=" ")
            temp = temp.next
        print()
        print("column_postion:", end=" ")
        while r != None:
            print(r.col, end=" ")
            r = r.next
        print()
        print("Value:", end=" ")
        while s != None:
            print(s.data, end=" ")
            s = s.next
        print()

# Driver Code
if __name__ == "__main__":

    # Creating Object
    s = Sparse()

    # Assuming 4x5 Sparse Matrix
    sparseMatric = [[0, 0, 3, 0, 4],
                    [0, 0, 5, 7, 0],
                    [0, 0, 0, 0, 0],
                    [0, 2, 6, 0, 0]]
    for i in range(4):
        for j in range(5):

            # Creating Linked List by only those
            # elements which are non-zero
            if sparseMatric[i][j] != 0:
                s.create_new_node(i, j, sparseMatric[i][j])

    # Printing the Linked List Representation
    # of the sparse matrix
    s.PrintList()

    # This code is contributed by Naveen Rathore

C#

// C# program for sparse matrix representation.
// Using Link list
using System;

class Program
{

    // Creating head/first node of list as NULL
    static Node first = null;

    // Node class to represent link list
    public class Node {
        public int row;
        public int col;
        public int data;
        public Node next;
    };

    // Driver Code
    static void Main(string[] args)
    {
        // 4x5 sparse matrix
        int[, ] sparseMatrix = { { 0, 0, 3, 0, 4 },
                                 { 0, 0, 5, 7, 0 },
                                 { 0, 0, 0, 0, 0 },
                                 { 0, 2, 6, 0, 0 } };

        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 5; j++) {
                // Pass only those values which
                // are non - zero
                if (sparseMatrix[i, j] != 0) {
                    create_new_node(i, j,
                                    sparseMatrix[i, j]);
                }
            }
        }
        printList(first);
    }

    // Function to create new node
    private static void
    create_new_node(int row_index, int col_index, int x)
    {
        Node temp = first;
        Node r;

        // If link list is empty then
        // create first node and assign value.
        if (temp == null) {
            temp = new Node();
            temp.row = row_index;
            temp.col = col_index;
            temp.data = x;
            temp.next = null;
            first = temp;
        }

        // If link list is already created
        // then append newly created node
        else

        {
            while (temp.next != null)
                temp = temp.next;

            r = new Node();
            r.row = row_index;
            r.col = col_index;
            r.data = x;
            r.next = null;
            temp.next = r;
        }
    }

    // Function prints contents of linked list
    // starting from start
    public static void printList(Node start)
    {
        Node ptr = start;
        Console.Write("row_position:");
        while (ptr != null) {
            Console.Write(ptr.row + " ");
            ptr = ptr.next;
        }
        Console.WriteLine("");
        Console.Write("column_position:");
        ptr = start;
        while (ptr != null) {
            Console.Write(ptr.col + " ");
            ptr = ptr.next;
        }
        Console.WriteLine("");
        Console.Write("Value:");
        ptr = start;
        while (ptr != null) {
            Console.Write(ptr.data + " ");
            ptr = ptr.next;
        }
    }
}

// This code is contributed by Tapesh (tapeshdua420)

Javascript

// JS Program for Representation of
// Sparse Matrix into Linked List

// Node Class to represent Linked List Node
class Node
{
    constructor(row, col, data)
    {
        this.row = row;
        this.col = col;
        this.data = data;
        this.next = null;
    }
}

// Class to convert Sparse Matrix
// into Linked List
class Sparse
{

    // Initialize Class Variables
    constructor()
    {
        this.head = null
        this.temp = null
        this.size = 0
    }

    // Function which returns the size
    // of the Linked List
    len()
    {
        return this.size
    }

    // Check the Linked List is
    // Empty or not
    isempty()
    {
        return this.size == 0
    }

    // Responsible function to create
    // Linked List from Sparse Matrix
    create_new_node(row, col, data)
    {
        // Creating New Node
        let newNode = new Node(row, col, data)

        // Check whether the List is
        // empty or not
        if (this.isempty())
            this.head = newNode
        else
            (this.temp).next = newNode
        this.temp = newNode

        // Incrementing the size
        this.size += 1
    }

    // Function display the contents of
    // Linked List
    PrintList()
    {
        let temp = this.head
        let r = this.head
        let s = this.head

        process.stdout.write("row_position: ")
        while (temp != null)
        {
            process.stdout.write(temp.row + " ")
            temp = temp.next
        }
        console.log()
        process.stdout.write("column_postion: ")
        while (r != null)
        {
            process.stdout.write(r.col + " " )
            r = r.next
        }
        console.log()
        process.stdout.write("Value: ")
        while (s != null)
        {
            process.stdout.write(s.data + " ")
            s = s.next
        }
        console.log()
    }
}

// Driver Code

// Creating Object
let s = new Sparse()

// Assuming 4x5 Sparse Matrix
let sparseMatric = [[0, 0, 3, 0, 4],
                    [0, 0, 5, 7, 0],
                    [0, 0, 0, 0, 0],
                    [0, 2, 6, 0, 0]]

for (var i = 0; i < 4; i++)
    for (var j = 0; j < 5; j++)
        // Creating Linked List by only those
        // elements which are non-zero
        if (sparseMatric[i][j] != 0)
        {
            s.create_new_node(i, j, sparseMatric[i][j])
            s.data = sparseMatric[i][j]
        }





// Printing the Linked List Representation
// of the sparse matrix
s.PrintList()

Output

row_position:0 0 1 1 3 3 
column_position:2 4 2 3 1 2 
Value:3 4 5 7 2 6 

Time Complexity:  O(N*M), where N is the number of rows in the sparse matrix, and M is the number of columns in the sparse matrix.
Auxiliary Space: O(1)

Other representations:

As a Dictionary where row and column numbers are used as keys and values are matrix entries. This method saves space but sequential access of items is costly.

As a list of list. The idea is to make a list of rows and every item of list contains values. We can keep list items sorted by column numbers.
Sparse Matrix and its representations | Set 2 (Using List of Lists and Dictionary of keys)

This article is contributed by Akash Gupta.If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.