Sorted order printing of a given array that represents a BST

Given an array that stores a complete Binary Search Tree, write a function that efficiently prints the given array in ascending order. 
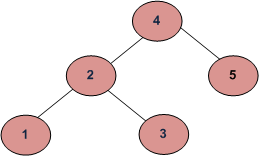
For example, given an array [4, 2, 5, 1, 3], the function should print 1, 2, 3, 4, 5 

Solution:

Inorder traversal of BST prints it in ascending order. The only trick is to modify recursion termination condition in standard Inorder Tree Traversal.

Implementation:

C++

// C++ Code for Sorted order printing of a
// given array that represents a BST
#include<bits/stdc++.h>
using namespace std;

void printSorted(int arr[], int start, int end)
{
    if(start > end)
        return;

    // print left subtree
    printSorted(arr, start*2 + 1, end);

    // print root
    cout << arr[start] << " ";

    // print right subtree
    printSorted(arr, start*2 + 2, end);
}

int main()
{
    int arr[] = {4, 2, 5, 1, 3};
    int arr_size = sizeof(arr)/sizeof(int);
    printSorted(arr, 0, arr_size-1);
    getchar();
    return 0;
}

// This code is contributed by Akanksha Rai

C

// C Code for Sorted order printing of a
// given array that represents a BST
#include<stdio.h>

void printSorted(int arr[], int start, int end)
{
  if(start > end)
    return;

  // print left subtree
  printSorted(arr, start*2 + 1, end);

  // print root
  printf("%d  ", arr[start]);

  // print right subtree
  printSorted(arr, start*2 + 2, end);
}

int main()
{
  int arr[] = {4, 2, 5, 1, 3};
  int arr_size = sizeof(arr)/sizeof(int);
  printSorted(arr, 0, arr_size-1);
  getchar();
  return 0;
}

Java

// JAVA Code for Sorted order printing of a
// given array that represents a BST
class GFG{

private static void printSorted(int[] arr, int start,
                                        int end) {
        if(start > end)
            return;

        // print left subtree
        printSorted(arr, start*2 + 1, end);

        // print root
        System.out.print(arr[start] + " ");

        // print right subtree
        printSorted(arr, start*2 + 2, end);
        }

    // driver program to test above function
    public static void main(String[] args) {
        int arr[] = {4, 2, 5, 1, 3};

        printSorted(arr, 0, arr.length-1);
    }
}

// This code is contributed by Arnav Kr. Mandal.

Python3

# Python3 Code for Sorted order printing of a
# given array that represents a BST
def printSorted(arr, start, end):
    if start > end:
        return

    # print left subtree
    printSorted(arr, start * 2 + 1, end)

    # print root
    print(arr[start], end = " ")

    # print right subtree
    printSorted(arr, start * 2 + 2, end)

# Driver Code
if __name__ == '__main__':
    arr = [4, 2, 5, 1, 3]
    arr_size = len(arr)
    printSorted(arr, 0, arr_size - 1)

# This code is contributed by PranchalK

C#

// C# Code for Sorted order printing
// of a given array that represents a BST
using System;

class GFG
{
static private void printSorted(int []arr,
                                int start,
                                int end)
{
    if(start > end)
        return;

    // print left subtree
    printSorted(arr, start * 2 + 1, end);

    // print root
    Console.Write(arr[start] + " ");

    // print right subtree
    printSorted(arr, start * 2 + 2, end);
    }

// Driver Code
static public void Main(String []args)
{
    int []arr= {4, 2, 5, 1, 3};

    printSorted(arr, 0, arr.Length - 1);
}
}

// This code is contributed by Arnab Kundu

PHP

<?php
// PHP Code for Sorted order printing of a
// given array that represents a BST

function printSorted($arr, $start, $end)
{
    if($start > $end)
        return;

    // print left subtree
    printSorted($arr, $start * 2 + 1, $end);

    // print root
    echo($arr[$start] . " ");

    // print right subtree
    printSorted($arr, $start * 2 + 2, $end);
}

// Driver Code
$arr = array(4, 2, 5, 1, 3);

printSorted($arr, 0, sizeof($arr) - 1);

// This code is contributed by Code_Mech.

Javascript

<script>

// Javascript Code for Sorted order printing of a
// given array that represents a BST
function printSorted(arr, start, end)
{
    if (start > end)
        return;

    // Print var left subtree
    printSorted(arr, start * 2 + 1, end);

    // Print var root
    document.write(arr[start] + " ");

    // Print var right subtree
    printSorted(arr, start * 2 + 2, end);
}

// Driver code
var arr = [4, 2, 5, 1, 3];

printSorted(arr, 0, arr.length - 1);

// This code is contributed by shikhasingrajput

</script>

Output

1 2 3 4 5 

Time Complexity: O(n), As we are visiting every element just once.
Auxiliary Space: O(h), Here h is the height of the tree and the extra space is used in the recursion call stack.

Please write comments if you find the above solution incorrect, or find better ways to solve the same problem.