Smallest subsequence with sum of absolute difference of consecutive elements maximized
Last Updated :
13 Dec, 2021
Given an array arr[] of length N, containing values in the range [1, N], the task is to find a subsequence s1, s2, …, sk such that
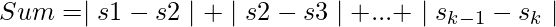
is maximised. In case of multiple subsequences having maximum possible sum, print the smallest one.
Input: N = 3, P = {3, 2, 1}
Output: K = 2, S = {3, 1}
Explanation:
Maximum sum possible = 2
Subsequences {3, 2, 1} and {3, 1} achieves that sum.
Hence, the subsequence {3, 1} is considered being of smaller length.
Input: N = 4, P = {1, 3, 4, 2}
Output: K = 3, S = {1, 4, 2}
Explanation:
Maximum sum possible = 5
Subsequences {1, 3, 4, 2} and {1, 4, 2} achieves that sum.
Hence, the subsequence {1, 4, 2} is considered being of smaller length.
Naive Approach:
Generate all subsequences of length >= 2 and calculate their respective sums. Keep track of the maximum sum obtained for any subsequence. In the case of multiple subsequences having the maximum sum, keep updating the minimum length, and maintain that subsequence. Finally print the subsequence.
Time Complexity: O(2N)
Efficient Approach:
There are a few key observations that will help us proceed:
- The maximum sum will be obtained when all the elements in the permutation are considered.
For example:
N = 4, P = [1, 3, 4, 2]
Max sum = | 1 – 3 | + | 3 – 4 | + | 4 – 2 | = 2 + 1 + 2 = 5
Here, the length is N and the required subsequence is permutation P itself.
Now that we know the maximum possible sum, the objective is to minimize the subsequence length without affecting this maximum sum.- For a monotonically increasing or decreasing subsequence, maximum sum can be achieved by only considering the First and Last element, for example:
S = [1, 3, 5, 7]
Max sum = | 1 – 3 | + | 3 – 5 | + | 5 – 7 | = 2 + 2 + 2 = 6, K = 4
Considering only first and last element,
S = [1, 7]
Max sum = | 1 – 7 | = 6, K = 2
In this way, the length of the subsequence can be reduced without affecting the Max sum.
Hence, from the given array, keep extracting the end-points of monotonically increasing or decreasing subsequences, and add them to the subsequence in the following way:
- The first and the last element of the permutation are default endpoints
- An element P[ i ] is a monotonically increasing endpoint if P[ i – 1 ] < P[ i ] > P[ i + 1 ]
- An element P[ i ] is monotonically decreasing endpoint if P[ i – 1 ] > P[ i ] < P[ i + 1 ]
The subsequence thus obtained will have maximum sum and minimum length.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void getSubsequence(vector<int>& arr,
int n)
{
vector<int> req;
req.push_back(arr[0]);
for (int i = 1; i < n - 1; i++) {
if (arr[i] > arr[i + 1]
&& arr[i] > arr[i - 1])
req.push_back(arr[i]);
else if (arr[i] < arr[i + 1]
&& arr[i] < arr[i - 1])
req.push_back(arr[i]);
}
req.push_back(arr[n - 1]);
cout << req.size() << endl;
for (auto x : req)
cout << x << " ";
}
int main()
{
vector<int> arr = { 1, 2, 5, 3,
6, 7, 4 };
int n = arr.size();
getSubsequence(arr, n);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void getSubsequence(int []arr, int n)
{
Vector<Integer> req = new Vector<Integer>();
req.add(arr[0]);
for(int i = 1; i < n - 1; i++)
{
if (arr[i] > arr[i + 1] &&
arr[i] > arr[i - 1])
req.add(arr[i]);
else if (arr[i] < arr[i + 1] &&
arr[i] < arr[i - 1])
req.add(arr[i]);
}
req.add(arr[n - 1]);
System.out.print(req.size() + "\n");
for(int x : req)
System.out.print(x + " ");
}
public static void main(String[] args)
{
int []arr = { 1, 2, 5, 3,
6, 7, 4 };
int n = arr.length;
getSubsequence(arr, n);
}
}
|
Python3
def getSubsequence(arr, n):
req = []
req.append(arr[0])
for i in range(1, n - 1):
if (arr[i] > arr[i + 1] and
arr[i] > arr[i - 1]):
req.append(arr[i])
elif (arr[i] < arr[i + 1] and
arr[i] < arr[i - 1]):
req.append(arr[i]);
req.append(arr[n - 1]);
print(len(req))
for x in req:
print(x, end = ' ')
if __name__=='__main__':
arr = [ 1, 2, 5, 3, 6, 7, 4 ]
n = len(arr)
getSubsequence(arr, n)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static void getSubsequence(int []arr, int n)
{
List<int> req = new List<int>();
req.Add(arr[0]);
for(int i = 1; i < n - 1; i++)
{
if (arr[i] > arr[i + 1] &&
arr[i] > arr[i - 1])
req.Add(arr[i]);
else if (arr[i] < arr[i + 1] &&
arr[i] < arr[i - 1])
req.Add(arr[i]);
}
req.Add(arr[n - 1]);
Console.Write(req.Count + "\n");
foreach(int x in req)
Console.Write(x + " ");
}
public static void Main(String[] args)
{
int []arr = { 1, 2, 5, 3,
6, 7, 4 };
int n = arr.Length;
getSubsequence(arr, n);
}
}
|
Javascript
<script>
function getSubsequence(arr, n)
{
let req = [];
req.push(arr[0]);
for (let i = 1; i < n - 1; i++) {
if (arr[i] > arr[i + 1]
&& arr[i] > arr[i - 1])
req.push(arr[i]);
else if (arr[i] < arr[i + 1]
&& arr[i] < arr[i - 1])
req.push(arr[i]);
}
req.push(arr[n - 1]);
document.write(req.length + '<br>');
for (let x of req)
document.write(x + " ");
}
let arr = [1, 2, 5, 3,
6, 7, 4];
let n = arr.length;
getSubsequence(arr, n);
</script>
|
Time complexity: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...