Smallest power of 2 consisting of N digits
Last Updated :
20 Oct, 2022
Given an integer N, the task is to find the smallest power of 2 which consists of N digits.
Examples:
Input: N = 3
Output: 7
Explanation:
27 = 128, which has three digits.
Input: N = 4
Output: 10
Explanation:
210 = 1024, which has four digits.
Naive Approach: A simple solution is to iterate through all the powers of 2 starting from 20 and check for each power of 2, if it contains N digits or not. Print the first power of two which contains N digits.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int smallestNum(int n)
{
int res = 1;
for (int i = 2;; i *= 2) {
int length = log10(i) + 1;
if (length == n)
return log(i) / log(2);
}
}
int main()
{
int n = 4;
cout << smallestNum(n);
return 0;
}
|
Java
import java.io.*;
class GFG{
static int smallestNum(int n)
{
int res = 1;
for(int i = 2;; i *= 2)
{
int length = (int)(Math.log10(i)) + 1;
if (length == n)
return (int)(Math.log(i) /
Math.log(2));
}
}
public static void main (String[] args)
{
int n = 4;
System.out.print(smallestNum(n));
}
}
|
Python3
from math import log10, log
def smallestNum(n):
res = 1
i = 2
while (True):
length = int(log10(i) + 1)
if (length == n):
return int(log(i) // log(2))
i *= 2
n = 4
print(smallestNum(n))
|
C#
using System;
class GFG{
static int smallestNum(int n)
{
for(int i = 2;; i *= 2)
{
int length = (int)(Math.Log10(i)) + 1;
if (length == n)
return (int)(Math.Log(i) /
Math.Log(2));
}
}
public static void Main ()
{
int n = 4;
Console.Write(smallestNum(n));
}
}
|
Javascript
<script>
function smallestNum(n)
{
res = 1;
for (var i = 2;; i *= 2) {
var length = parseInt(Math.log(i)/Math.log(10)) + 1;
if (length == n)
return parseInt(Math.log(i) / Math.log(2));
}
}
n = 4;
document.write(smallestNum(n));
</script>
|
Time Complexity: O(log2n)
Auxiliary Space: O(1)
Efficient Approach: The key observation to optimize the above approach is that the smallest power of 2 with N digits can be obtained by the equation:
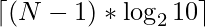
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int smallestNum(int n)
{
float power = log2(10);
cout<<power;
return ceil((n - 1) * power);
}
int main()
{
int n = 4;
cout << smallestNum(n);
return 0;
}
|
Java
class GFG{
static int smallestNum(int n)
{
double power = log2(10);
return (int) Math.ceil((n - 1) * power);
}
static double log2(int N)
{
return (Math.log(N) / Math.log(2));
}
public static void main(String[] args)
{
int n = 4;
System.out.print(smallestNum(n));
}
}
|
Python3
from math import log2, ceil
def smallestNum(n):
power = log2(10)
print(power);
return ceil((n - 1) * power)
n = 4
print(smallestNum(n))
|
C#
using System;
class GFG{
static int smallestNum(int n)
{
double power = log2(10);
return (int) Math.Ceiling((n - 1) * power);
}
static double log2(int N)
{
return (Math.Log(N) / Math.Log(2));
}
public static void Main()
{
int n = 4;
Console.Write(smallestNum(n));
}
}
|
Javascript
<script>
function smallestNum(n)
{
let power = log2(10);
return Math.ceil((n - 1) * power);
}
function log2(N)
{
return (Math.log(N) / Math.log(2));
}
let n = 4;
document.write(smallestNum(n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...