Smallest positive integer X satisfying the given equation

Read

Discuss

Given two integers N and K, the task is to find the smallest positive integer X satisfying the equation:

(X / K) * (X % K) = N

Examples:

Input: N = 6, K = 3
Output: 11
Explanation:
For X = 11, (11 / 3) * (11 % 3) = 3 * 2 = 6
Therefore, the following equation satisfies.

Input: N = 4, K = 6
Output: 10
Explanation:
For X = 10, (10 / 6) * (10 % 6) = 1 * 4 = 4
Therefore, the following equation satisfies.

Brute Force Approach:

The brute force approach to solve this problem would be to iterate over all positive integers X and check if the given equation is satisfied. If the equation is satisfied for any value of X, we return that value as the smallest positive integer satisfying the equation.

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
using namespace std;
 
// Function to find out the smallest
// positive integer for the equation
int findMinSoln(int n, int k)
{
    int x = 1;
    while (true) {
        if ((x / k) * (x % k) == n) {
            return x;
        }
        x++;
    }
}
 
// Driver Code
int main()
{
    int n = 4, k = 6;
    cout << findMinSoln(n, k);
    return 0;
}

Java

public class Main {
    // Function to find out the smallest
    // positive integer for the equation
    public static int findMinSoln(int n, int k) {
        int x = 1;
        while (true) {
            if ((x / k) * (x % k) == n) {
                return x;
            }
            x++;
        }
    }
 
    // Driver Code
    public static void main(String[] args) {
        int n = 4, k = 6;
        System.out.println(findMinSoln(n, k));
    }
}

Python3

# Function to find out the smallest
# positive integer for the equation
def findMinSoln(n, k):
    x = 1
    while True:
        if (x // k) * (x % k) == n:
            return x
        x += 1
 
# Driver Code
if __name__ == '__main__':
    n, k = 4, 6
    print(findMinSoln(n, k))

C#

// C# Program to implement
// the above approach
using System;
 
class GFG
{
    // Function to find out the smallest
    // positive integer for the equation
    static int FindMinSoln(int n, int k)
    {
        int x = 1;
 
        while (true)
        {
            // Check if (x / k) * (x % k) is equal to n
            if ((x / k) * (x % k) == n)
            {
                return x; // If condition is met, return the value of x
            }
 
            x++; // Increment x by 1 for the next iteration
        }
    }
//Driver Code
    static void Main()
    {
        int n = 4, k = 6;
        int result = FindMinSoln(n, k);
        Console.WriteLine(result); // Output the result
    }
}

Javascript

// Function to find out the smallest
// positive integer for the equation
function findMinSoln(n, k) {
  let x = 1;
 
  while (true) {
    // Check if (x / k) * (x % k) is equal to n
    if ((Math.floor(x / k) * (x % k)) === n) {
      return x; // If condition is met, return the value of x
    }
 
    x++; // Increment x by 1 for the next iteration
  }
}
 
// Driver Code
  const n = 4;
  const k = 6;
  const result = findMinSoln(n, k);
  console.log(result); // Output the result

Output

Time Complexity: O(X), which can be very large if X is a large number.
Auxiliary Space : O(1)

Approach:

The idea is to observe that, since (X / K) * (X % K) = N, therefore, N will be divisible by p = X % K, which is less than K. Therefore, for all i in the range [1, K) try all values of p where:

$x = p \cdot\frac{n - p}{k}$

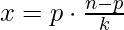
Below is the implementation of the above approach:

C++

// C++ Program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find out the smallest
// positive integer for the equation
int findMinSoln(int n, int k)
{
    // Stores the minimum
    int minSoln = INT_MAX;
 
    // Iterate till K
    for (int i = 1; i < k; i++) {
 
        // Check if n is divisible by i
        if (n % i == 0)
            minSoln
                = min(minSoln, (n / i) * k + i);
    }
 
    // Return the answer
    return minSoln;
}
 
// Driver Code
int main()
{
    int n = 4, k = 6;
    cout << findMinSoln(n, k);
}

Java

// Java Program to implement
// the above approach
import java.util.*;
class GFG{
  
// Function to find out the smallest
// positive integer for the equation
static int findMinSoln(int n, int k)
{
    // Stores the minimum
    int minSoln = Integer.MAX_VALUE;
  
    // Iterate till K
    for (int i = 1; i < k; i++) 
    {
  
        // Check if n is divisible by i
        if (n % i == 0)
            minSoln = Math.min(minSoln, (n / i) * k + i);
    }
  
    // Return the answer
    return minSoln;
}
  
// Driver Code
public static void main(String[] args)
{
    int n = 4, k = 6;
    System.out.println(findMinSoln(n, k));
}
}
 
// This code is contributed by Ritik Bansal

Python3

# Python3 program to implement
# the above approach
import sys
 
# Function to find out the smallest
# positive integer for the equation
def findMinSoln(n, k):
     
    # Stores the minimum
    minSoln = sys.maxsize;
 
    # Iterate till K
    for i in range(1, k):
 
        # Check if n is divisible by i
        if (n % i == 0):
            minSoln = min(minSoln, (n // i) * k + i);
     
    # Return the answer
    return minSoln;
 
# Driver Code
if __name__ == '__main__':
     
    n = 4;
    k = 6;
     
    print(findMinSoln(n, k));
 
# This code is contributed by amal kumar choubey 

C#

// C# program to implement
// the above approach
using System;
 
class GFG{
 
// Function to find out the smallest
// positive integer for the equation
static int findMinSoln(int n, int k)
{
     
    // Stores the minimum
    int minSoln = int.MaxValue;
 
    // Iterate till K
    for (int i = 1; i < k; i++) 
    {
 
        // Check if n is divisible by i
        if (n % i == 0)
            minSoln = Math.Min(minSoln,
                              (n / i) * k + i);
    }
 
    // Return the answer
    return minSoln;
}
 
// Driver Code
public static void Main(String[] args)
{
    int n = 4, k = 6;
     
    Console.WriteLine(findMinSoln(n, k));
}
}
 
// This code is contributed by amal kumar choubey 

Javascript

<script>
 
 
// Javascript Program to implement
// the above approach
 
// Function to find out the smallest
// positive integer for the equation
function findMinSoln(n, k)
{
 
    // Stores the minimum
    var minSoln = 1000000000;
 
    // Iterate till K
    for (var i = 1; i < k; i++) {
 
        // Check if n is divisible by i
        if (n % i == 0)
            minSoln
                = Math.min(minSoln, (n / i) * k + i);
    }
 
    // Return the answer
    return minSoln;
}
 
// Driver Code
var n = 4, k = 6;
document.write( findMinSoln(n, k));
 
// This code is contributed by rutvik_56.
</script>