Smallest number whose square has N digits
Last Updated :
24 Jun, 2021
Given a number N, the task is to find the smallest number whose square has N digits.
Examples:
Input: N = 2
Output: 4
Explanation:
32 = 9, which has 1 digit.
42 = 16, which has 2 digits.
Hence, 4 is the smallest number whose square has N digits.
Input: N = 3
Output: 10
Explanation:
102 = 100, which has 3 digits.
Naive Approach: The simplest approach to solve the problem is to calculate the square of each number starting from and count the number of digits in its square. Print the first number whose square is obtained to be of N digits.
Time Complexity: O(?(10N))
Efficient Approach: To solve the problem, we need to make the following observations:
The smallest number whose square has 1 digit = 1
The smallest number whose square has 2 digits = 4
The smallest number whose square has 3 digits = 10
The smallest number whose square has 4 digits = 32
The smallest number whose square has 5 digits = 100
Hence, these numbers form a series 1, 4, 10, 32, 100, 317, …….
Now, we need to find a formula for the Nth term of the series.
The terms of the series can be expressed in the following form:
If N = 1, Smallest number possible is 1.
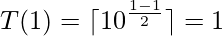
If N = 2, Smallest number possible is 41.
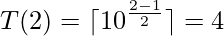
If N = 3, Smallest number possible is 10.
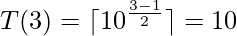
Hence, we can conclude that the Nth of the series can be expressed as
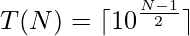
Hence, in order to solve the problem, we just need to calculate ceil(10(N – 1)/ 2) for the given integer N.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int smallestNum(int N)
{
float x = pow(10.0, (N - 1) / 2.0);
return ceil(x);
}
int main()
{
int N = 4;
cout << smallestNum(N);
return 0;
}
|
Java
class GFG{
static int smallestNum(int N)
{
float x = (float)(Math.pow(10, (N - 1) / 2.0));
return (int)(Math.ceil(x));
}
public static void main(String[] args)
{
int N = 4;
System.out.print(smallestNum(N));
}
}
|
Python3
import math;
def smallestNum(N):
x = pow(10.0, (N - 1) / 2.0);
return math.ceil(x);
N = 4;
print(smallestNum(N));
|
C#
using System;
class GFG{
static int smallestNum(int N)
{
float x = (float)(Math.Pow(10, (N - 1) / 2.0));
return (int)(Math.Ceiling(x));
}
public static void Main()
{
int N = 4;
Console.Write(smallestNum(N));
}
}
|
Javascript
<script>
function smallestNum(N)
{
x = Math.pow(10.0, (N - 1) / 2.0);
return Math.ceil(x);
}
let N = 4;
document.write(smallestNum(N));
</script>
|
Time Complexity: O(log(N))
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...