Smallest number with sum of digits as N and divisible by 10^N
Last Updated :
18 Nov, 2022
Find the smallest number such that the sum of its digits is N and it is divisible by 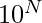 .
.
Examples :
Input : N = 5
Output : 500000
500000 is the smallest number divisible
by 10^5 and sum of digits as 5.
Input : N = 20
Output : 29900000000000000000000
Explanation: To make a number divisible by 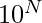 we need at least N zeros at the end of the number. To make the number smallest, we append exactly N zeros to the end of the number. Now, we need to ensure the sum of the digits is N. For this, we will try to make the length of the number as small as possible to get the answer. Thus we keep on inserting 9 into the number till the sum doesn’t exceed N. If we have any remainder left, then we keep it as the first digit (a most significant one) so that the resulting number is minimized.
we need at least N zeros at the end of the number. To make the number smallest, we append exactly N zeros to the end of the number. Now, we need to ensure the sum of the digits is N. For this, we will try to make the length of the number as small as possible to get the answer. Thus we keep on inserting 9 into the number till the sum doesn’t exceed N. If we have any remainder left, then we keep it as the first digit (a most significant one) so that the resulting number is minimized.
The approach works well for all subtasks but there are 2 corner cases:
- The first is that the final number may not fit into the data types present in C++/Java. Since we only need to output the number, we can use strings to store the answer.
- The only corner case where the answer is 0 is N = 0.
- There are no cases where the answer doesn’t exist.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
void digitsNum(int N)
{
if (N == 0)
cout << "0\n";
if (N % 9 != 0)
cout << (N % 9);
for (int i = 1; i <= (N / 9); ++i)
cout << "9";
for (int i = 1; i <= N; ++i)
cout << "0";
cout << "\n";
}
int main()
{
int N = 5;
cout << "The number is : ";
digitsNum(N);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static void digitsNum(int N)
{
if (N == 0)
System.out.println("0");
if (N % 9 != 0)
System.out.print((N % 9));
for (int i = 1; i <= (N / 9); ++i)
System.out.print("9");
for (int i = 1; i <= N; ++i)
System.out.print("0");
System.out.print("" );
}
public static void main (String[] args)
{
int N = 5;
System.out.print("The number is : ");
digitsNum(N);
}
}
|
Python3
import math
def digitsNum(N):
if (N == 0) :
print("0", end = "")
if (N % 9 != 0):
print (N % 9, end ="")
for i in range( 1, int(N / 9) + 1) :
print("9", end = "")
for i in range(1, N + 1) :
print("0", end = "")
print()
N = 5
print("The number is : ",end="")
digitsNum(N)
|
C#
using System;
class GFG
{
static void digitsNum(int N)
{
if (N == 0)
Console.Write("0");
if (N % 9 != 0)
Console.Write((N % 9));
for (int i = 1; i <= (N / 9); ++i)
Console.Write("9");
for (int i = 1; i <= N; ++i)
Console.Write("0");
Console.WriteLine("" );
}
public static void Main ()
{
int N = 5;
Console.Write("The number is : ");
digitsNum(N);
}
}
|
PHP
<?php
function digitsNum($N)
{
if ($N == 0)
echo "0\n";
if ($N % 9 != 0)
echo ($N % 9);
for ( $i = 1; $i <= ($N / 9); ++$i)
echo "9";
for ($i = 1; $i <= $N; ++$i)
echo "0";
echo "\n";
}
$N = 5;
echo "The number is : ";
digitsNum($N);
?>
|
Javascript
<script>
function digitsNum(N)
{
if (N == 0) document.write("0\n");
if (N % 9 != 0) document.write(N % 9);
for (var i = 1; i <= N / 9; ++i) document.write("9");
for (var i = 1; i <= N; ++i) document.write("0");
document.write("\n");
}
var N = 5;
document.write("The number is : ");
digitsNum(N);
</script>
|
OutputThe number is : 500000
Time Complexity: O(N), where N is the given input.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...