Slope formula is used to determine the steepness or inclination of a line. The x and y coordinates of the points lying on the line are used to calculate the slope of a line. The change in the “y” coordinate concerning the change in the “x” coordinates is called the slope of a line, and it is usually depicted by the letter “m”. Using the slope formula, we can determine whether two lines are perpendicular, parallel, or collinear.
Slope formula is required to calculate the inclination of a line. For calculating the slope of a line, x and y coordinates of the points on the line are required. The ratio of change in y coordinates and change in x coordinates is called the slope of a line.
Slope (m) = change in y/change in x = Δy/Δx
In mathematics, the slope of a line is used to determine how much the line has inclined, i.e., the steepness of a line. To determine the slope of a line, we need the x and y coordinates of the points lying on the line. The slope formula is the net change in the “y” coordinate divided by the net change in the “x” coordinate. Δy is the change in the “y” coordinates, and Δx is the change in the “x” coordinates. Hence, the ratio of the change in “y” coordinates with respect to the change in the “x” coordinates is given by,
Slope (m) = change in y/change in x = Δy/Δx
m= (y2 – y1)/(x2 – x1)
where
- x1 and x2 are the coordinates of the X-axis
- y1 and y2 are the coordinates of the Y-axis
The x and y coordinates of the line are used to calculate the slope of the line. The net change in the y coordinate is Δy, while the net change in the x coordinate is Δx. So the change in y coordinate with respect to the change in the x coordinate can be written as,
m = Δy/Δx
where,
- m is the slope
- Δy is the change in y-coordinates
- Δx is the change in the x-coordinates
We know that tan θ is also the slope of the line where θ is the angle made by the line with the positive direction of the x-axis.
And, tan θ = height/base
Since the height/base between any two given points = (y2 – y1)/(x2 – x1)
Thus, the slope equation is, m = tan θ = Δy/Δx
From the graph, we observe:
Δy = (y2 – y1)
Δx = (x2 – x1)
Then, the slope formula is given as: Slope = m = (y2 – y1)/(x2 – x1)
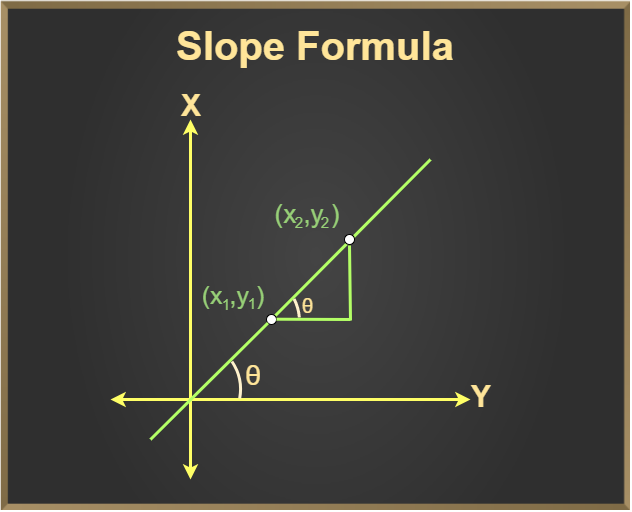
- We know that tan θ is also a slope of the line hence the slope of a line can also be represented as,
Slope (m) = tan θ = Δy/Δx
Where θ is the angle made by the line w.r.t to the positive X-axis,
- Δy = change in the “y” coordinates,
- Δx = change in the “x” coordinates.
- We can also define the slope of a line as the ratio of rising with respect to run.
Slope (m) = Rise/Run
- Let ax + by + c = 0 be the general equation of a line. Now, the formula for the slope of the line is given by,
Slope (m) = – coefficient of x / coefficient of y = -a/b
- The slope-intercept form of a line using the line equation is given as,
y = mx + c
Where m is the slope of the line and c is the y-intercept of the line.
Slope Equation
Slope formula is used to determine the slope of a line. The equation that is used in finding the slope is written as:
m = tanθ = Δy/Δx = (y2 – y1)/(x2 – x1)
where,
- m is slope of line
- Δy is the difference in y-coordinates
- Δx is the difference in the x-coordinates
- θ is angle made by the line with the positive x-axis
Equation of line with slope m is given by,
y = mx + c
where,
- m is slope of the line
- b is y-intercept of the line
Read More,
Example 1: Find the slope of a line whose coordinates are (3, 7) and (5, 8).
Solution:
Given, (x1, y1) = (3,7) and (x2, y2) = (5,8)
Slope formula (m) = (y2 – y1)/(x2 – x1)
⇒ m = (8 – 7)/(5 – 3) = 1/2
Hence, the slope of the given line is 1/2.
Example 2: Determine the slope of a line whose coordinates are (7, -5) and (2, -3).
Solution:
Given, (x1, y1) = (7, -5) and (x2, y2) = (2, -3)
Slope formula (m) = (y2 – y1)/(x2 – x1)
⇒ m = (-3 – (-5))/(2 – 7) = -2/5
Hence, the slope of the given line is -2/5
Example 3: Find the value of a, if the slope of a line passing through the points (-4, a) and (2, 5) is 3.
Solution:
Given, (x1, y1) = (4,a) and (x2, y2) = (2, 5) and slope (m) = 3
We know that slope (m) = (y2 – y1)/(x2 – x1)
⇒ 3 = (5 – a)/(2 – 4)
⇒ 3 = (5 – a)/(-2)
⇒ -6 = 5 – a ⇒ a = 5 + 6 = 11
Hence, the value of a = 11
Example 4: If a line makes an angle of 60° with the positive Y-axis, then what is the value of the slope of the line?
Solution:
Given data, Angle made by a line with the positive y-axis = 60°
We know that if the line makes an angle of 60° from the positive y-axis, then it makes an angle of (90° – 60° = 30°) with the x-axis.
Therefore, the value of the slope of the line (m) = tan 30° = 1/√3
Hence, the value of the slope of the line = 1/√3.
Example 5: Sheela was checking a graph, and she noticed that the raise was 12 units and the run was 4 units. Now calculate the slope of a line.
Solution:
Given data, rise = 12 units and run = 4 units
We know that slope (m) = rise/run
⇒ m = 12/4 = 3
Hence, the slope of the given line is 3
Example 6: Find the slope of the line 3x – 7y + 8 = 0.
Solution:
Given data, The equation of the line = 3x – 7y + 8 = 0
Now, compare the given with the general equation of the line i.e., ax + by + c = 0
Therefore, a = 3, b = -7 and c = 8
We know that Slope (m) = – coefficient of x/coefficient of y = -a/b
⇒ m = -3/(-7) = 3/7
Hence, the slope of the given line is 3/7.
Q1: What is the Slope of a Line?
Slope of a line, is the value of the steepness or the inclination of a line in x-y plane. Slope is calculated using different methods, depending upon whether the equation of the line or the coordinates of points on the line is given.
Q2: What is the formula to find the Slope of a tangent formula?
Slope of a line is calculated using the given formula. Suppose the given coordinates of two points lying on the line be (x1 , y1)/(x2 , y2). Then the formula is given as, Slope = m = tan θ = (y2 – y1)/(x2 – x1)
Q3: What is the slope formula definition?
Slope formula is defined as,
- Slope = (Change in y coordinate)/(Change in x coordinate)
- Slope = rise/run.
Q4: What is the slope of a graph formula?
Slope of a line is the measure of its inclination with positive x axis. Mathematically, the slope is defined as “rise over run”.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...