Sliding friction is friction that acts on objects when they are sliding over a surface. Sliding friction is weaker than static friction. That’s why it’s easier to slide a piece of furniture over the floor after you start it moving than it is to get it moving in the first place. Sliding friction can be useful. For example, you use sliding friction when you write with a pencil. The pencil “lead” slides easily over the paper, but there’s just enough friction between the pencil and paper to leave a mark.
Example: How does sliding friction help you ride a bike?
There is sliding friction between the brake pads and bike rims each time you use your bike’s brakes. This friction slows the rolling wheels so you can stop.
Some more examples of sliding friction can be
- Sledding
- Pushing an object across a surface
- Rubbing one’s hands together (The friction force generates heat.)
- A car sliding on ice
- A car skidding as it turns a corner
- Opening a window
- Almost any motion where there is contact between an object and a surface
Factors affecting Sliding friction
The factors affecting sliding friction can be written in points as

The surface deformation of objects.
Friction exists in liquid and gases also. Friction is less in air or water compared to when sliding against a solid surface like road.
The roughness or smoothness of the surface of the objects.
Smooth surfaces slide over surfaces easily compared to rough ones. When you look at the microscopic scale you can notice the irregularities in the surface which hinder sliding. Thus, more the roughness higher is the friction
The original speed of either object.
The increase in surface temperature leads to gradual flattening of the protrusions, resulting in steady state and higher slide speed at high temperature, which reduce the shear force, reduce the coefficient of friction, and attain low roughness
The size of the object.
The weight of any object is the commonly observed force in the normal direction. So, friction is directly proportional to the weight of an object
Finally, the amount of pressure on either object.
The force in the normal direction (perpendicular to the sliding plane) will increase the interaction between the surface thus increasing the friction. Friction is thus directly proportional to the normal force applied.
Sliding Friction Formula
The equation for sliding force includes the coefficient of sliding friction times the normal force.
Fs = μsFn
Where,
Fs = Force of sliding friction
μs = Coefficient of sliding friction
Fn= normal force
Derivation for Coefficient of friction
Perpendicular force reduced
When an object is placed on an incline, the force perpendicular between the surfaces is reduced, according to the angle of the incline. The force required to overcome friction (Fr) equals the coefficient of friction (μ) times the cosine of the incline angle (cos θ) times the weight of the object (W). There are mathematical tables that give the values of cosines for various angles.
Fr = μ W Cosθ
Gravity contributes to sliding
Note that when an object is on an incline, the force of gravity contributes to causing the object to slide down the ramp or incline. Let’s call that force (Fg), and it is equal to the weight of the object (W) times the sine of the angle (sin θ)
Fg = W sin θ
Tangent of angle determines coefficient
If you put the ramp at a steep enough angle, Fg will become greater than Fr and the object will slide down the incline. The angle at which it just starts to slide is determined from the equation:
μ W cos θ = W sin θ
Dividing both sides of the equation by W and cos θ, we get the equation for the static coefficient of friction
μ = tan θ
where tan θ is the tangent of angle θ and equals 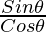 .
.
Motion on an Inclined Surface
The inclined plane is a problem set in which a massive object is on a slope, and only subject to motion in the direction down the incline. Although gravity pulls an object straight down, the presence of the slope prevents this. Because objects can’t move through the solid surface of the incline, the object is limited to movement along the surface of the incline.
For example: If you put a book on a ramp and changed the angle of the ramp until the book started to slide and then measured the angle of the ramp, you could determine the coefficient of friction between the book and the ramp. If the angle was 30 degrees, then the tangent of 30 degrees is about 0.58. That would be the static coefficient of friction in this case. Even if you increased the weight on the book, it would still slide at 30 degrees.

Normal Force
The normal force in an inclined plane is not directed in the direction that we are accustomed to. Up until now, we have always seen normal force directed upwards in the direction opposite to the force of gravity. The truth about normal forces is that they are not always upwards, but rather that they are always directed perpendicular to the surface that the object is on.
Gravity Force Components
To determine the net force acting upon an object on an inclined plane is difficult because the two forces acting on the body are not in opposite directions. To simplify, one of the forces acting on the object will have to be resolved into perpendicular components so that they can be easily added to other forces acting on the object.
The force that is directed at an angle to the horizontal is resolved into horizontal and vertical components. In the case of inclined planes, we resolve the weight vector (Fgrav) into two components. The force of gravity will be resolved into two components of force – one directed parallel to the inclined surface and the other-directed perpendicular to the inclined surface.
The diagram below shows how the force of gravity has been replaced by two components – a parallel and a perpendicular component of force.

From the figure, we understand that the perpendicular component of the force of gravity is directed in the opposite direction of normal force, balancing the normal force.
The parallel component of the force of gravity is not balanced by any other force. The object will subsequently accelerate down the inclined plane due to the presence of an unbalanced force. It is the parallel component of the force of gravity that causes this acceleration. The parallel component of the force of gravity is the net force.
Examples of Sliding Friction
- Rubbing both hands together to create heat.
- A child sliding down through a slide in a park.
- A coaster sliding against a table.
- A washing machine pushed along with the floor.
- The frame and the edge of the door sliding against one another.
- A block being slid across the floor.
- Two cards in a deck sliding against each other.
Sliding can occur between two objects of arbitrary shape whereas the rolling friction is the Frictional force that is associated with the rotational movement. The rolling friction is usually less than the one associated with sliding kinetic friction. The values for the coefficient of rolling friction are quite less than that of sliding friction. It usually produces greater sound and thermal bi-products.
Example: Movement of braking motor vehicle tires on a roadway.

Sample Problems on Sliding Friction
Question 1. The free-body diagram shows the forces acting upon a 100-kg crate that is sliding down an inclined plane. The plane is inclined at an angle of 30 degrees. The coefficient of friction between the crate and the incline is 0.3. Determine the net force and acceleration of the crate.

Solution:
The force of gravity in the given problem can be calculated as:
F = 9.8 × 100 = 980 N
The components of the force of gravity can be determined as follows:
Fparallel = 980 × sin30° = 490 N
Fperpendicular = 980 × cos30° = 849 N
As the perpendicular component of the weight vector balances the normal force, the value of the weight vector is 849 N
The value of the frictional force can be determined by multiplying the value of normal force and the coefficient of friction.
Fnorm = 0.3 × 849 = 255 N
The net force is the vector sum of all the forces acting on the body.
The net force can be calculated as follows:
490 N – 255 N = 235 N
The acceleration is calculated as follows:
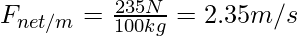
Question 2. Coefficient of sliding friction on a body is 0.5 and the normal force applied is 200 N. Find the force due to sliding friction.
Solution:
N = 200 N
μ = 0.5
F= μ × N
F = 0.5 × 200 N = 100 N
So, sliding friction applied on body is 100N.
Question 3. What does sliding friction depend on?
Answer:
Sliding friction depends only on two variables: the materials in question and the weight of the object.
Changing the surface area in contact does not change the sliding friction. Sliding friction for most materials is less than the static friction.
Question 4: What are some examples of sliding friction?
Answer:
Examples of sliding friction
1. Sledding.
2. Pushing an object across a surface.
3. Rubbing one’s hands together (The friction force generates heat.)
4. A car sliding on ice.
5. A car skidding as it turns a corner.
6. Opening a window.
7. Almost any motion where there is contact between an object and a surface.
Question 5. Is sliding friction constant?
Answer:
Although it may seem counterintuitive, the coefficient of sliding friction is independent of the area of the surfaces in contact, provided the normal force is constant. This holds only when the surfaces are hard and not lubricated.
Question 6. Which is less sliding friction or static friction?
Answer:
The friction between the two surfaces is because of the interlocking of the irregularities of the two surfaces.
During sliding, contact points do not get enough time to get interlocked properly. Therefore, less friction is generated than static friction. This explains why sliding friction is less than static friction.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...