Size of smallest square that contains N non-overlapping rectangles of given dimensions
Last Updated :
23 Apr, 2021
Given two positive integers W and H and N rectangles of dimension W*H, the task is to find the smallest size of the square required such that all the N rectangles can be packed without overlapping.
Examples:
Input: N = 10, W = 2, H = 3
Output: 9
Explanation:
The smallest size of the square is 9 units to pack the given 10 rectangles of size 2*3 as illustrated in the below image:

Input: N = 1, W = 3, H = 3
Output: 3
Approach: The given problem is based on the following observations:
- It can be shown that one of the optimal spacing of rectangles within a square is given by:
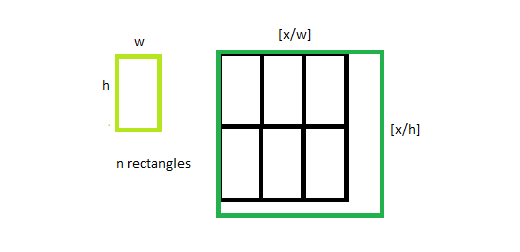
- The maximum number of rectangles of dimension W*H, that can be fitted in the square with sides X is given by ?X/W???X/H?.
- The above function is monotonically increasing. Therefore, the idea is to use the Binary Search to find the smallest side of a square that satisfies the given condition.
Follow the steps below to solve the problem:
- Initialize two variables, say low as 1, and high as W*H*N.
- Iterate until i is less than j and perform the following steps:
- Find the value of mid as (i + j)/2.
- Now, if the value (mid/W)*(mid/H) is at most N, then update the value of high as mid.
- Otherwise, update the value of low as (mid + 1).
- After completing the above steps, print the value of high as the resultant value.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
bool bound(int w, int h, int N, int x)
{
int val = (x / w) * (x / h);
if (val >= N)
return true;
else
return false;
}
int FindSquare(int N, int W, int H)
{
int i = 1;
int j = W * H * N;
while (i < j)
{
int mid = i + (j - i) / 2;
if (bound(W, H, N, mid))
j = mid;
else
i = mid + 1;
}
return j;
}
int main()
{
int W = 2;
int H = 3;
int N = 10;
cout << FindSquare(N, W, H);
}
|
Java
class GFG{
static boolean bound(int w, int h, int N, int x)
{
int val = (x / w) * (x / h);
if (val >= N)
return true;
else
return false;
}
static int FindSquare(int N, int W, int H)
{
int i = 1;
int j = W * H * N;
while (i < j)
{
int mid = i + (j - i) / 2;
if (bound(W, H, N, mid))
j = mid;
else
i = mid + 1;
}
return j;
}
public static void main(String[] args)
{
int W = 2;
int H = 3;
int N = 10;
System.out.print(FindSquare(N, W, H));
}
}
|
Python3
def bound(w, h, N, x):
val = (x//w)*(x//h)
if(val >= N):
return True
else:
return False
def FindSquare(N, W, H):
i = 1
j = W * H*N
while(i < j):
mid = i + (j - i)//2
if(bound(W, H, N, mid)):
j = mid
else:
i = mid + 1
return j
W = 2
H = 3
N = 10
print(FindSquare(N, W, H))
|
C#
using System;
class GFG{
static bool bound(int w, int h, int N, int x)
{
int val = (x / w) * (x / h);
if (val >= N)
return true;
else
return false;
}
static int FindSquare(int N, int W, int H)
{
int i = 1;
int j = W * H * N;
while (i < j)
{
int mid = i + (j - i) / 2;
if (bound(W, H, N, mid))
j = mid;
else
i = mid + 1;
}
return j;
}
public static void Main()
{
int W = 2;
int H = 3;
int N = 10;
Console.WriteLine(FindSquare(N, W, H));
}
}
|
Javascript
<script>
function bound(w, h, N, x)
{
let val = parseInt(x / w) * parseInt(x / h);
if (val >= N)
return true;
else
return false;
}
function FindSquare(N, W, H)
{
let i = 1;
let j = W * H * N;
while (i < j)
{
let mid = i + parseInt((j - i) / 2);
if (bound(W, H, N, mid))
j = mid;
else
i = mid + 1;
}
return j;
}
let W = 2;
let H = 3;
let N = 10;
document.write(FindSquare(N, W, H));
</script>
|
Time Complexity: O(log(W*H))
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...