Prerequisites: Matrix Diagonalization, Eigenvector Computation and Low-Rank Approximations
Before getting in depth into the SVD, let us first briefly understand what Matrix Diagonalization technique is and when it fails to perform efficiently.
Matrix Diagonalization
Matrix diagonalization is the process of taking a square matrix and converting it into a special type of matrix known as the diagonal matrix. This matrix shares the same fundamental properties of the underlying matrix. Mathematically, any input matrix A can be reduced into any diagonal matrix D if it satisfies:
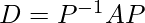
where,
P -> Modal Matrix: It is a (n x n) matrix that consists of eigen-vectors.
It is generally used in the process of diagonalization
and similarity transformation.
However, the matrix diagonalization technique fails for matrices of the form (m x n) where m ≠ n. (i.e. when the matrix is not a square matrix. This is where ‘Singular Value Decomposition’ comes into picture and provides a good solution to this problem.
Singular Values (σ)
Let A be any m x n matrix with rank r. On multiply it with its transpose (i.e. ATA), a n x n matrix is created which is symmetric as well as positive semi-definite in nature. In simpler terms, all the Eigen values (λi…r) of ATA matrix are non-negative (i.e. greater than 0).
The singular values are defined as the square root of the obtained Eigen values. That is:
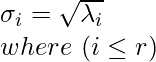
Singular Value Decomposition (SVD)
Let A be any m x n matrix. Then the SVD divides this matrix into 2 unitary matrices that are orthogonal in nature and a rectangular diagonal matrix containing singular values till r. Mathematically, it is expressed as:
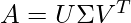
where,
Σ -> (m x n) diagonal matrix where the elements of the diagonal are the singular values
U -> (m x m) orthogonal matrix whose columns are the left singular vectors
V -> (n x n) orthogonal matrix whose columns are the right singular vectors
Now, It is important to understand how to calculate the matrices U, V & Σ.
Calculating normalized eigeinvectors
First, we calculate the Eigen vectors xi associated of a square matrix X. Then, we find the normalized eiegnvectors vi corresponding to the eigenvectors xi by dividing each value in vector xi by its magnitude. For example:
Let x = [1,2,4]
=> mag(x) or |x| = √(12 + 22 + 42) = √21.
Therefore, v = [(1/√21), (2/√21), (4/√21)]
Calculating orthogonal matrix V
We know, A is a m x n matrix. Therefore, ATA is a n x n symmetric matrix with all Eigen values > 0. So, we can obtain Eigen vectors v1…n of ATA such that:
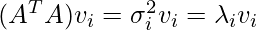
where,
xi -> eigen vector
vi -> normalized eigen vector.
and
σi -> corresponding singular value.
λi -> corresponding eigen value.
Upon calculating the Eigen vectors of AAT, matrix V will be:
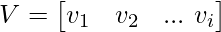
where, v1, v2, ... vi are arranged column-wise into matrix V.
Calculating orthogonal matrix U
Similarly, for any A (m x n) matrix, AAT is a m x m symmetric matrix with all eigen values > 0. So, we can obtain eigen vectors x1…n of AAT such that:
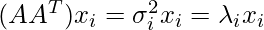
where,
xi -> eigen vector.
and
σi -> corresponding singular value.
λi -> corresponding eigen value.
Now, we use the following equation to compute matrix U:
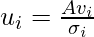
Upon calculating, matrix U will be:
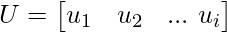
where, u1, u2, ... ui are arranged column-wise into matrix U.
Calculating diagonal matrix Σ
Here, matrix A has rank(A) = r where r ≤ min (m,n).
Case 1: If m ≤ n, say m = 2 & n = 4, then assuming all (σi > 0), Σ can be expressed as:
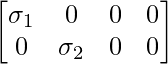
Case 2: If m ≥ n, say m = 5 & n = 3, then assuming all (σi > 0), Σ can be expressed as:

Special Case: When rank of matrix is specified, say r = 3, m = 6 & n = 4. Then Σ can be expressed as:

This implies that σ4 ≤ 0, hence discarded.
NOTE: The number of singular values where σi > 0 can determine the rank of the matrix.
Example Problem
Consider the following problem. Find the SVD of a (2 x 3) matrix A having values:
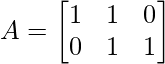
Solution
Let us understand each step required for solving such problems.
Step 1 - Find AT and then compute ATA.
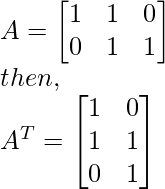
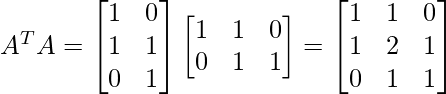
Step 2 - Find the eigen values associated with matrix ATA.
(Discussed in the prerequisite articles mentioned above)
Eigen values associated with ATA: λ = 0, 1 & 3.
Step 3 - Find the singular values corresponding to the obtained
eigen values using formula:
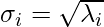
Singular values associated with ATA: λ = 3, 1 & 0.
λ1 = 3 -> σ1 = √3
λ2 = 1 -> σ2 = 1
λ3 = 0 -> σ3 = 0
Step 4 - Compute diagonal matrix Σ using the values of σ keeping
the above discussed cases in mind.
As (m = 2 < n = 3), Case 1 is applied and matrix Σ is:
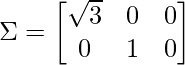
Step 5 - Find the eigen vectors & corresponding normalized eigen vectors
associated with matrix ATA.
(Discussed in the prerequisite articles mentioned above)
NOTE: It is important to understand that normalized eigen vectors of ATA define the matrix V.
Eigen vectors associated with ATA:
For λ1 = 3 -> x1 = [1, 2, 1]
For λ2 = 1 -> x2 = [-1, 0, 1]
For λ3 = 0 -> x3 = [1, -1, 1]
where x1, x2 and x3 are eigen vectors of matrix ATA.
Normalized eigen vectors associated with ATA:
For x1 = [1, 2, 1] => v1 = [(1/√6), (2/√6), (1/√6)]
For x2 = [-1, 0, 1] => v2 = [(-1/√2), 0, (1/√2)]
For x3 = [1, -1, 1] => v3 = [(1/√3), (-1/√3), (1/√3)]
where v1, v2 and v3 are eigen vectors of matrix ATA.
Step 6 - Use eigen vectors obtained to compute matrix V.
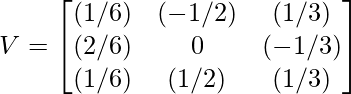
Step 7 - Use the above given equation to compute the orthogonal matrix U.
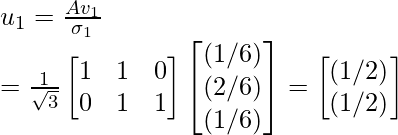
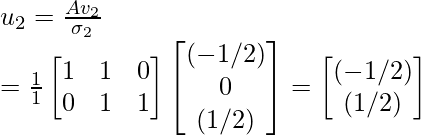
Therefore, orthogonal matrix U is:
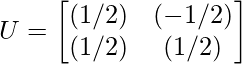
Step 8 - Compute the SVD of A using the equation given below:
(As discussed above)
Therefore, using SVD, A can be expressed as:
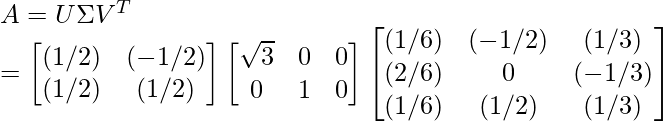
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...