Sine Rule with Derivation, Example and Implementation
Last Updated :
13 Jul, 2021
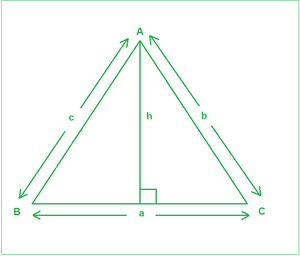
Given angles(in degrees) A, C, and the side c, corresponding to the figure below, the task is to find the remaining two sides a and b.
Examples:
Input: A = 45, C = 35, c = 23
Output:
28.35
39.49
Explanation:
a is 28.35 and b is 39.49
Input: A = 45, C = 45, c = 10
Output:
10
14.14
Approach: The idea is to use Sine rule. It states that the sides of any triangle are proportional to the sine of the angles opposite to them. a / Sin(A) = b / Sin(B) = c / Sin(C). The derivation is described below:
As is evident from the figure above:
A perpendicular of length h has been drawn on BC from A. From General trigonometric rules:
SinB=h/c——–(1)
SinC=h/b——–(2)
From the above two equations, we get:
c x SinB=b x SinC
Or b/SinB=c/SinC—–(3)
Similarly, if a perpendicular is drawn from B to AC, we can get:
a/SinA=c/SinC——-(4)
From Equations (3) and (4), we get:
a/SinA=b/SinB=c/SinC
Follow the steps below to solve the problem:
- Change the angles A and C from degrees to radians to be able to be used in the inbuilt functions.
- Calculate the angle B using the observation that sums of angles of a triangle sums up to 180 degrees.
- Use the Sine rule to calculate the sides a and b.
Below is the implementation of the above approach:
C++14
#include <bits/stdc++.h>
using namespace std;
void findSides(double A, double C, double c)
{
double B = 180 - (A + C);
A = A * (3.14159 / 180);
C = C * (3.14159 / 180);
B = B * (3.14159 / 180);
double a = (c / sin(C)) * sin(A);
double b = (c / sin(C)) * sin(B);
cout << fixed << setprecision(2);
cout << a << endl;
cout << b << endl;
}
int main()
{
double A = 45.0;
double C = 35.0;
double c = 23;
findSides(A, C, c);
return 0;
}
|
Java
class GFG{
static void findSides(double A, double C,
double c)
{
double B = 180 - (A + C);
A = A * (3.14159 / 180);
C = C * (3.14159 / 180);
B = B * (3.14159 / 180);
double a = (c / Math.sin(C)) * Math.sin(A);
double b = (c / Math.sin(C)) * Math.sin(B);
System.out.println(String.format("%.2f", a));
System.out.println(String.format("%.2f", b));
}
public static void main(String[] args)
{
double A = 45.0;
double C = 35.0;
double c = 23;
findSides(A, C, c);
}
}
|
Python3
import math
def findSides(A, C, c):
B = 180 - (A + C)
A = A * (3.14159 / 180)
C = C * (3.14159 / 180)
B = B * (3.14159 / 180)
a = (c / math.sin(C)) * math.sin(A)
b = (c / math.sin(C)) * math.sin(B)
print("{0:.2f}".format(a))
print("{0:.2f}".format(b))
A = 45.0
C = 35.0
c = 23
findSides(A, C, c)
|
C#
using System;
class GFG{
static void findSides(double A, double C,
double c)
{
double B = 180 - (A + C);
A = A * (3.14159 / 180);
C = C * (3.14159 / 180);
B = B * (3.14159 / 180);
double a = (c / Math.Sin(C)) * Math.Sin(A);
double b = (c / Math.Sin(C)) * Math.Sin(B);
Console.WriteLine("{0:F2}",a);
Console.WriteLine("{0:F2}",b);
}
public static void Main(String[] args)
{
double A = 45.0;
double C = 35.0;
double c = 23;
findSides(A, C, c);
}
}
|
Javascript
<script>
function findSides(A, C, c)
{
let B = 180 - (A + C);
A = A * (3.14159 / 180);
C = C * (3.14159 / 180);
B = B * (3.14159 / 180);
let a = (c / Math.sin(C)) * Math.sin(A);
let b = (c / Math.sin(C)) * Math.sin(B);
document.write(a.toPrecision(4) + "<br>");
document.write(b.toPrecision(4) + "<br>");
}
let A = 45.0;
let C = 35.0;
let c = 23;
findSides(A, C, c);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...