Simplified International Data Encryption Algorithm (IDEA)
Last Updated :
01 Nov, 2023
Introduction :
The International Data Encryption Algorithm (IDEA) is a symmetric-key block cipher that was first introduced in 1991. It was designed to provide secure encryption for digital data and is used in a variety of applications, such as secure communications, financial transactions, and electronic voting systems.
IDEA uses a block cipher with a block size of 64 bits and a key size of 128 bits. It uses a series of mathematical operations, including modular arithmetic, bit shifting, and exclusive OR (XOR) operations, to transform the plaintext into ciphertext. The cipher is designed to be highly secure and resistant to various types of attacks, including differential and linear cryptanalysis.
One of the strengths of IDEA is its efficient implementation in software and hardware. The algorithm is relatively fast and requires only a small amount of memory and processing power. This makes it a popular choice for use in embedded systems and other applications where resources are limited.
IDEA has been widely used in various encryption applications, although it has been largely replaced by newer encryption algorithms such as AES (Advanced Encryption Standard) in recent years. However, IDEA is still considered to be a highly secure and effective encryption algorithm, and it continues to be used in some legacy systems and applications.
In cryptography, block ciphers are very important in the designing of many cryptographic algorithms and are widely used to encrypt the bulk of data in chunks. By chunks, it means that the cipher takes a fixed size of the plaintext in the encryption process and generates a fixed size ciphertext using a fixed-length key. An algorithm’s strength is determined by its key length.
The Simplified International Data Encryption Algorithm (IDEA) is a symmetric key block cipher that:
- uses a fixed-length plaintext of 16 bits and
- encrypts them in 4 chunks of 4 bits each
- to produce 16 bits ciphertext.
- The length of the key used is 32 bits.
- The key is also divided into 8 blocks of 4 bits each.
This algorithm involves a series of 4 identical complete rounds and 1 half-round. Each complete round involves a series of 14 steps that includes operations like:
- Bitwise XOR
- Addition modulo
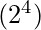
- Multiplication modulo
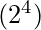 +1
+1
After 4 complete rounds, the final “half-round” consists of only the first 4 out of the 14 steps previously used in the full rounds. To perform these rounds, each binary notation must be converted to its equivalent decimal notation, perform the operation and the result obtained should be converted back to the binary representation for the final result of that particular step.
Key Schedule: 6 subkeys of 4 bits out of the 8 subkeys are used in each complete round, while 4 are used in the half-round. So, 4.5 rounds require 28 subkeys. The given key, ‘K’, directly gives the first 8 subkeys. By rotating the main key left by 6 bits between each group of 8, further groups of 8 subkeys are created, implying less than one rotation per round for the key (3 rotations).

|
| Round 1 | 1101 | 1100 | 0110 | 1111 | 0011 | 1111 |
| Round 2 | 0101 | 1001* | 0001 | 1011 | 1100 | 1111 |
| Round 3 | 1101 | 0110 | 0111 | 0111* | 1111 | 0011 |
| Round 4 | 1111 | 0101 | 1001 | 1101 | 1100 | 0110* |
| Round 4.5 | 1111 | 1101 | 0110 | 0111 | | |
* denotes a shift of bits
Notations used in the 14 steps:
|
| * | Multiplication modulo 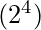 +1 +1 |
| + | Addition modulo 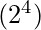 |
| ^ | Bitwise XOR |
The 16-bit plaintext can be represented as X1 || X2 || X3 || X4, each of size 4 bits. The 32-bit key is broken into 8 subkeys denoted as K1 || K2 || K3 || K4 || K5 || K6 || K7 || K8, again of size 4 bits each. Each round of 14 steps uses the three algebraic operation-Addition modulo (2^4), Multiplication modulo (2^4)+1 and Bitwise XOR. The steps involved are as follows:
- X1 * K1
- X2 + K2
- X3 + K3
- X4 * K4
- Step 1 ^ Step 3
- Step 2 ^ Step 4
- Step 5 * K5
- Step 6 + Step 7
- Step 8 * K6
- Step 7 + Step 9
- Step 1 ^ Step 9
- Step 3 ^ Step 9
- Step 2 ^ Step 10
- Step 4 ^ Step 10
The input to the next round is Step 11 || Step 13 || Step 12 || Step 14, which becomes X1 || X2 || X3 || X4. This swap between 12 and 13 takes place after each complete round, except the last complete round (4th round), where the input to the final half round is Step 11 || Step 12 || Step 13 || Step 14.
After last complete round, the half-round is as follows:
- X1 * K1
- X2 + K2
- X3 + K3
- X4 * K4
The final output is obtained by concatenating the blocks.
Example:
Key: 1101 1100 0110 1111 0011 1111 0101 1001
Plaintext: 1001 1100 1010 1100
Ciphertext: 1011 1011 0100 1011
Explanation:
The explanation is only for 1st complete round (the remaining can be implemented similarly) and the last half-round.
- Round 1:
- From the plaintext: X1 – 1001, X2 – 1100, X3 – 1010, X4 – 1100
- From the table above: K1 – 1101, K2 – 1100, K3 – 0110, K4 – 1111, K5 – 0011, K6 – 1111
(1001(9) * 1101(13))(mod 17) = 1111(15)
(1100(12) + 1100(12))(mod 16) = 1000(8)
(1010(10) + 0110(6))(mod 16) = 0000(0)
(1100(12) * 1111(15))(mod 17) = 1010(10)
(1111(15) ^ 0000(0)) = 1111(15)
(1000(8) ^ 1010(10)) = 0010(2)
(1111(15) * 0011(3))(mod 17) = 1011(11)
(0010(2) + 1011(11))(mod 16) = 1101(13)
(1101(13) * 1111(15))(mod 17) = 1000(8)
(1011(11) + 1000(8))(mod 16) = 0011(3)
(1000(8) ^ 1111(15)) = 0111(7)
(1000(8) ^ 0000(0)) = 1000(8)
(0011(3) ^ 1000(8)) = 1011(11)
(0011(3) ^ 1010(10)) = 1001(9)
- Round 1 Output: 0111 1011 1000 1001 (Step 12 and Step 13 results are interchanged)
- Round 2:
- From Round 1 output: X1 – 0111, X2 – 1011, X3 – 1000, X4 – 1001
- From the table above: K1 – 0101, K2 – 1001, K3 – 0001, K4 – 1011, K5 – 1100, K6 – 1111
- Round 2 Output: 0110 0110 1110 1100 (Step 12 and Step 13 results are interchanged)
- Round 3:
- From Round 2 Output: X1 – 0110, X2 – 0110, X3 – 1110, X4 – 1100
- From the table above: K1 – 1101, K2 – 0110, K3 – 0111, K4 – 0111, K5 – 1111, K6 – 0011
- Round 3 Output: 0100 1110 1011 0010 (Step 12 and Step 13 results are interchanged)
- Round 4:
- From Round 3 Output: X1 – 0100, X2 – 1110, X3 – 1011, X4 – 0010
- From the table above: K1 – 1111, K2 – 0101, K3 – 1001, K4 – 1101, K5 – 1100, K6 – 0110
- Round 4 Output: 0011 1110 1110 0100 (Step 12 and Step 13 results are interchanged)
- Round 4.5:
- From Round 4 Output: X1 – 0011, X2 – 1110, X3 – 1110, X4 – 0100
- From the table above: K1 – 1111, K2 – 1101, K3 – 0110, K4 – 0111
- Round 4.5 Output: 1011 1011 0100 1011 (Step 2 and Step 3 results are not interchanged)
(0011(3) * 1111(15))(mod 17) = 1011(11)
(1110(14) + 1101(13))(mod 16) = 1011(11)
(1110(14) + 0110(6))(mod 16) = 0100(4)
(0100(4) * 0111(7))(mod 17) = 1011(11)
- Final Ciphertext is 1011 1011 0100 1011
NOTE: For every round except the final transformation, a swap occurs, and the input is given to the next round
Uses of International Data Encryption Algorithm (IDEA) :
Some of the common uses of IDEA include:
- Secure communication: IDEA can be used to encrypt data transmitted over communication networks such as the internet, providing confidentiality and protecting against unauthorized access.
- Financial transactions: IDEA can be used to secure financial transactions such as online banking and credit card transactions, helping to prevent identity theft and fraud.
- Electronic voting systems: IDEA can be used to encrypt votes in electronic voting systems, providing secure and confidential voting.
- File encryption: IDEA can be used to encrypt files and folders on a computer or other storage device, protecting them from unauthorized access.
- Password protection: IDEA can be used to encrypt passwords and other sensitive information stored on a computer or network, helping to prevent unauthorized access and data breaches.
Issues in International Data Encryption Algorithm (IDEA) :
- Key size: While IDEA uses a 128-bit key size, which is generally considered secure, it is still theoretically possible to brute-force the key if an attacker has enough computing power. This is why longer key sizes are often used in modern encryption algorithms.
- Patents: IDEA was originally patented, which limited its availability and adoption in certain countries. While the patent has since expired, this could still be a consideration for some organizations.
- Block size: IDEA has a fixed block size of 64 bits, which can limit its effectiveness in certain applications where larger block sizes are required.
- Implementation issues: Like any encryption algorithm, IDEA can be vulnerable to implementation issues such as side-channel attacks or implementation flaws. This highlights the importance of using best practices and careful implementation when using any encryption algorithm.
- Availability: While IDEA is still considered to be a strong and effective encryption algorithm, it has been largely replaced by newer algorithms such as AES in modern applications. This means that support and availability of IDEA implementations may become more limited over time.
Reference :
Here are some references for further reading on the International Data Encryption Algorithm (IDEA):
- Biham, E., & Shamir, A. (1991). Differential Cryptanalysis of the Data Encryption Standard. Springer Berlin Heidelberg.
- Massey, J. L., & Rueppel, R. A. (1994). New Directions in Cryptography. Springer-Verlag New York, Inc.
- Schneier, B. (1996). Applied Cryptography: Protocols, Algorithms, and Source Code in C. John Wiley & Sons, Inc.
- Stallings, W. (2017). Cryptography and Network Security: Principles and Practice. Pearson Education, Inc.
- IDEA Cipher Algorithm Description. (1999). Retrieved from https://www.cosic.esat.kuleuven.be/publications/article-113.pdf
- IDEA Encryption Algorithm. (n.d.). Retrieved from https://www.cryptopp.com/wiki/IDEA
- Meyer, C. H., & Matyas, S. M. (1994). Cryptography: A New Dimension in Computer Data Security. John Wiley & Sons, Inc.
Share your thoughts in the comments
Please Login to comment...