Similar Matrix

Last Updated : 26 Mar, 2023

A “matrix” is referred to as a rectangular array of numbers that are arranged in rows and columns. The horizontal lines are said to be rows, while the vertical lines are said to be columns. We can determine the size of a matrix by the number of rows and columns in it. If a matrix has “m” rows and “n” columns, then it is said to be an “m by n” matrix and is written as an “m × n” matrix. For example, a matrix with five rows and three columns is a “5 × 3” matrix. We have various types of matrices, like rectangular, square, triangular, symmetric, singular, etc. In this article, we learn about similar matrices, their examples, and their properties.

Similar Matrices

Two square matrices A and B of the same order are said to be similar, if and only if there exists an invertible matrix “P” of the same order as A and B such that:

P^-1AP = B

The transformation of the matrix A into “P^-1AP” is called similarity transformation or conjugation by “P,” as we are transforming the matrix “A” into the matrix “B.” Here, the matrix “P” is known as the change-of-basis matrix. If two matrices A and B are said to be similar, then they are expressed as A ∼ B.

Examples of Similar Matrices

The matrices given below are similar matrices of order “2 × 2” through the invertible matrix P of the same order.

$A = \left[\begin{array}{cc} 2 & 4\\ 0 & -2 \end{array}\right]$ and

$B = \left[\begin{array}{cc} 2 & 0\\ -4 & -2 \end{array}\right]$ are similar matrices through the invertible matrix P.

$P = \left[\begin{array}{cc} 2 & -2\\ 2 & 2 \end{array}\right]$

$P^{-1} = \frac{1}{4+4}\left[\begin{array}{cc} 2 & 2\\ -2 & 2 \end{array}\right] =\frac{1}{8}\left[\begin{array}{cc} 2 & 2\\ -2 & 2 \end{array}\right]$

$P^{-1} AP = \frac{1}{8}\left[\begin{array}{cc} 2 & 2\\ -2 & 2 \end{array}\right] × \left[\begin{array}{cc} 2 & 4\\ 0 & -2 \end{array}\right] × \left[\begin{array}{cc} 2 & -2\\ 2 & 2 \end{array}\right]$

$P^{-1} AP = \frac{1}{8}\left[\begin{array}{cc} 2 & 2\\ -2 & 2 \end{array}\right]\times\left[\begin{array}{cc} 12 & 4\\ -4 & -4 \end{array}\right]$

$P^{-1} AP = \frac{1}{8}\left[\begin{array}{cc} 16 & 0\\ -32 & -16 \end{array}\right]= \left[\begin{array}{cc} 2 & 0\\ -4 & -2 \end{array}\right] = B$

Properties of Similar Matrices

Following are some important properties of similar matrices A and B:

Ranks of two similar matrices are the same, i.e., the rank of A = rank of B.
Determinants of two similar matrices are the same, i.e., det (A) = det (B).
Trace of two similar matrices is the same, i.e., tr(A) = tr(B).
Eigenvalues of two similar matrices are the same, but their eigenvectors are normally different.
If A and B are two similar matrices, then Aⁿ and Bⁿ are also similar matrices.
A matrix and its transpose matrix are similar, i.e., A ∼ A^T.
Two similar matrices, A and B, are said to have the same characteristic polynomial.
A matrix “A” is similar to itself, i.e., the similarity of matrices is reflexive.

A = I^-1AI,

where the identity matrix “I” is the change-of-basis matrix.

If matrix A is similar to matrix B, then matrix B is said to be similar to matrix A, i.e., the similarity of matrices is symmetric.

P^-1AP = B

A = PBP^-1

If matrix A is similar to matrix B and matrix B is similar to matrix C, then matrix A is said to be similar to matrix C, i.e., the similarity of matrices is transitive.

Also, Check

Determinant of a Matrix
Inverse of a Matrix
Matrix Addition and Scalar Multiplication

Solved Examples on Similar Matrices

Example 1: Find the matrix B if A and B are similar matrices. If

$A = \left[\begin{array}{cc} 1 & 2\\ 3 & -1 \end{array}\right]$

$P = \left[\begin{array}{cc} 0 & 1\\ 2 & 3 \end{array}\right]$ .

Solution:

We know that if A and B are similar matrices, then P^-1AP = B.

P^-1 = Adj P/|P|

|P| = 0 × 3 − (1 × 2) = -2

$Adj P = \left[\begin{array}{cc} 3 & -1\\ -2 & 0 \end{array}\right]$

$P^{-1} = \frac{1}{-2} \left[\begin{array}{cc} 3 & -1\\ -2 & 0 \end{array}\right]$

$B = P^{-1} AP$

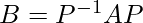
$B = \frac{1}{-2} \left[\begin{array}{cc} 3 & -1\\ -2 & 0 \end{array}\right]× \left[\begin{array}{cc} 1 & 2\\ 3 & -1 \end{array}\right]×\left[\begin{array}{cc} 0 & 1\\ 2 & 3 \end{array}\right]$

$B = \frac{1}{-2} \left[\begin{array}{cc} 3 & -1\\ -2 & 0 \end{array}\right]×\left[\begin{array}{cc} (0+4) & (1+6)\\ (0-2) & (3-3) \end{array}\right]$

$B = \frac{1}{-2} \left[\begin{array}{cc} 3 & -1\\ -2 & 0 \end{array}\right]×\left[\begin{array}{cc} 4 & 7\\ -2 & 0 \end{array}\right]$

$B = \frac{1}{-2} \left[\begin{array}{cc} 14 & 21\\ -8 & -14 \end{array}\right]$

$B = \left[\begin{array}{cc} \frac{14}{-2} & \frac{21}{-2}\\ \frac{-8}{-2} & \frac{-14}{-2} \end{array}\right]$

$B = \left[\begin{array}{cc} -7 & \frac{21}{-2}\\ 4 & 7 \end{array}\right]$

Example 2: Prove that the determinants of two similar matrices are the same.

Solution:

Let us consider two similar matrices A and B, to prove that their determinants are the same.

We know that if A and B are similar matrices, then P^-1AP = B, where P is the change-of-basis matrix.

Now, det (B) = det (P^-1AP)

⇒ det (B) = det (P^-1) det (A) det (P)

We know that det (P^-1) = 1/det (P)

So, det (B) = 1/det (P) × det (A) × det (P)

⇒ det (B) = 1 × det (A)

⇒ det (B) = det (A)

Hence, the determinants of two similar matrices A and B are the same.

Example 3: Prove that the matrix given below is similar to itself.

$A = \left[\begin{array}{ccc} 5 & 0 & 0\\ 0 & 3 & 0\\ 0 & 0 & 8 \end{array}\right]$

Solution:

To prove that a matrix is similar to itself, we have to prove that A = I^-1AI,

where the identity matrix “I” is the change-of-basis matrix.

$I = \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]$

I^-1 = Adj I/ det (I)

$I^{-1} =\frac{1}{1} \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]= \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]$

$I^{-1} AI = \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]×\left[\begin{array}{ccc} 5 & 0 & 0\\ 0 & 3 & 0\\ 0 & 0 & 8 \end{array}\right]× \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]$

$I^{-1} AI =\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]×\left[\begin{array}{ccc} 5 & 0 & 0\\ 0 & 3 & 0\\ 0 & 0 & 8 \end{array}\right]$

$I^{-1} AI = \left[\begin{array}{ccc} 5 & 0 & 0\\ 0 & 3 & 0\\ 0 & 0 & 8 \end{array}\right]= A$

Hence proved.

Example 4: Verify whether the matrices given below are similar or not.

$A = \left[\begin{array}{cc} 2 & 3\\ -1 & 4 \end{array}\right] and B = \left[\begin{array}{cc} 4 & -7\\ 8 & 10 \end{array}\right]$

$P = \left[\begin{array}{cc} 1 & 2\\ 3 & 4 \end{array}\right]$ .

Solution:

To prove that two matrices are similar, we have to prove that B = P^-1AP.

P^-1 = Adj P/|P|

$P^{-1} = \frac{1}{(8-6)}\left[\begin{array}{cc} 4 & -2\\ -3 & 1 \end{array}\right]$

$P^{-1} = \frac{1}{2}\left[\begin{array}{cc} 4 & -2\\ -3 & 1 \end{array}\right]$

$P^{-1} AP = \frac{1}{2}\left[\begin{array}{cc} 4 & -2\\ -3 & 1 \end{array}\right]\times\left[\begin{array}{cc} 2 & 3\\ -1 & 4 \end{array}\right]\times\left[\begin{array}{cc} 1 & 2\\ 3 & 4 \end{array}\right]$

$P^{-1} AP = \frac{1}{2}\left[\begin{array}{cc} 4 & -2\\ -3 & 1 \end{array}\right]\times\left[\begin{array}{cc} 8 & 16\\ 11 & 14 \end{array}\right]$

$P^{-1} AP = \frac{1}{2}\left[\begin{array}{cc} (32-22) & (64-28)\\ (-24+22) & (-48+14) \end{array}\right]$

$P^{-1} AP = \frac{1}{2}\left[\begin{array}{cc} 10 & 36\\ -2 & -34 \end{array}\right]$

$P^{-1} AP = \left[\begin{array}{cc} 5 & 18\\ -1 & -17 \end{array}\right]≠B$

As B ≠ P^-1AP, A and B are not similar.

FAQs on Similar Matrices

Question 1: What is meant by a matrix?

Answer:

A “matrix” is referred to as a rectangular array of numbers that are arranged in rows and columns. The horizontal lines are said to be rows, while the vertical lines are said to be columns.

Question 2: Define similar matrices.

Answer:

Two square matrices A and B of the same order are said to be similar, if and only if there exists an invertible matrix “P” of the same order as A and B such that:

P^-1AP = B

Question 3: Are the determinants of two similar matrices the same?

Answer:

Yes, two similar matrices A and B are said to have the same determinants, i.e., det (A) = det (B).

Suggest improvement

Find the volume of 64 cubes whose one side is 4cm

Row Matrix

Share your thoughts in the comments

Similar Matrix

Similar Matrices

Examples of Similar Matrices

Properties of Similar Matrices

Solved Examples on Similar Matrices

FAQs on Similar Matrices

Question 1: What is meant by a matrix?

Question 2: Define similar matrices.

Question 3: Are the determinants of two similar matrices the same?

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?